利用python实现灰色预测GM(1,1)

本篇内容的代码主要参考了：https://www.cnblogs.com/amoor/p/9719638.html

概述

灰色预测的优点不需要过多的数据集，理论上4个就足够了，所以更对分布规律根本不用关心。缺点在于只能适用于中短期的预测，对于长期预测还是很不准确的，比如S型曲线的前半段，有可能在灰色预测中被判定成指数增长。

GM(1,1)预测模型

GM(1,1)表示模型是一阶微分方程，且只含1个预测变量的灰色模型。造成一个一个结果的原因是多种多样的，他们占的权重我们有时也是无从只晓得的，但是再不出现意外的情况下，我们可以用结果去估计结果，这就是“灰因白果”，也就是下面介绍这种方法的目的。

预测方法

1. 设原始数据集为$x^{(0)}=(x^{(0)}(1),x^{(0)}(2),x^{(0)}(3),x^{(0)}(4),\cdots ,x^{(0)}(n))$。
2. 计算一次累加生成序列为$$x^{(1)}=(x^{(1)}(1),x^{(1)}(2),x^{(1)}(3),x^{(1)}(4),\cdots ,x^{(1)}(n))$$其中$$x^{(1)}(k)=\sum _{i=1}^k{x}^{(0)}(i)$$那么为什么要计算一个这样的序列呢？我感觉是为了让数据呈现出一定的增减趋势。原来的数据可能是无序的，但是如果这些数据都是非负的，那么他们的和就是一个非递减序列。同理都是负的也会有相应的变化，一正一负也有有相应的趋势，比如和都在0上或者都在0下。
3. 计算$x^{(1)}$的均值生成序列$$z^{(1)}=(z^{(1)}(2),z^{(1)}(3),z^{(1)}(4),\cdots ,z^{(1)}(n))$$，其中$z^{(1)}(k)=0.5\ast x^{(1)}(k)+0.5\ast x^{(1)}(k-1)$，注意$k取2，3，4，\cdots ,n$
   为什么要取均值呢？后面我会提出的我的想法。
4. 建立灰微分方程：$$x^{(0)}(k)+a{z}^{(1)}(k)=b,k=2,3,4,\cdots ,n$$这个灰微分方程我感觉，主要的目的就是为了得到一个第k个变量和前面k-1个变量的一堆线性方程。利用叠加求平均这种方式可能是为了让数据中的变量之间的差距缩小，为了后面用最小二乘法求最优解做准备。
5. 建立对应的白化微分方程，这个就是我们要预测的微分方程：之所以称之为白化，是因为预测出的结果是一个准确值即为白色的。$$\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}(t)=b$$
6. 根据步骤4给出的方程组，我们可以通过最小二乘法求出a、b的最优解
   $$\hat{u}=[\hat{a},\hat{b}{]}^T=(B^{T}B{)}^{-1}{B}^{T}Y$$
7. 求解方程，得到预测值：

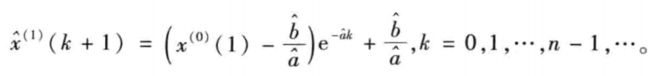
操作步骤和代码实现

我们选择一个例子来分析具体情节的操作方法：
例、北方某城市1986-1992年道路交通噪声平均声级数据见表，如下：

序号	年份	$L_{eq}$
1	1986	71.1
2	1987	72.4
3	1988	72.4
4	1989	72.1
5	1990	71.4
6	1991	72.0
7	1992	71.6

操作步骤

1. 要保证建模方法的可行性，首先要对数据进行级比检验，主要是不想让数据过于离谱。级比数列表达式如下：$$\lambda (k)=\frac{x^0(k-1)}{x^0(k)}$$如果$\lambda (k)$都落在$\Theta =(e^{-\frac{2}{n+1}},e^{-\frac{2}{n+2}})$如果没落在该区间内就平移一下数据数据就可以了。
   代码实现：

def check_data(x0):
    interval = [np.exp(-2/(len(x0)+1)),np.exp(2/(len(x0)+2))]
    getSeries = lambda k:x0[k-1]/x0[k]
    global lambda_k 
    lambda_k = [getSeries(i) for i in range(2,len(x0))]
    if min(lambda_k) > interval[0] and max(lambda_k)<interval[1]:
        return 0
    #计算出偏移量
    c = min(lambda_k)-interval[0] if min(lambda_k)-interval[0]<0 else max(lambda_k)-interval[1]
    return c

def offset(x0,c):
    y0 = x0-c
    return y0

2. 平移成功以后就可以开始构造相应矩阵$x_0,x_1,z_1,B,u,Y$:

 #计算AOG
    x0 = np.array(x0)
    x1 = np.cumsum(x0)
    #计算x1的均值生成序列
    x1 = pd.DataFrame(x1)
    z1 = (x1+x1.shift())/2.0#该项与该项的前一项相加除以2，用shift比循环代码更简单
    z1 = z1[1:].values.reshape((len(z1)-1,1))#再将刚刚算出的数据转成ndarray,删去nan
    B = np.append(-z1,np.ones_like(z1),axis=1)#合并数据形成B矩阵
    Y = x0[1:].reshape((len(x0)-1,1))#建立Y矩阵

3. 把值求解出来：

	#求出a,b的值
	[[a],[b]] = np.dot(np.dot((np.linalg.inv(np.dot(B.T,B))),B.T),Y)
    #方程求解 f(k+1)表示x1(k+1)
    f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2))
    #求出估计的所有x1的预测值,大小和x0一样
    x1_pre = [f(k) for k in range(1,len(x0)+1)]

4. 进行残差检验和级比检验，检验的公式如下所示：令$$\sigma (k)=\frac{x^0(k)-{\hat{x}}^0(k)}{x^0(k)}$$这里${\hat{x}}^{(0)}(1)=x^{(0)}(1)$，如果$\sigma (k)$小于0.2则说明可达到一般的需求，如果小于0.1则可达到较高的需求.
   级比检验的公式如下，$$\rho (k)=1-(\frac{1-0.5a}{1+0.5a})\lambda (k)$$如果$\rho (k)$小于0.2则说明可达到一般的需求，如果小于0.1则可达到较高的需求.
   代码实现：

    delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
    #检验预测值，利用残差检验
    residual_error = np.abs(x0-np.array(x1_pre))
    residual_error_max = residual_error.max
    #级比偏差值检验
    p = [1-((1-0.5*a)/(1+0.5*a))*l for l in lambda_k]

5. GM代码总结(主要是看着舒服)：

def GM1_1(x0):
    #验证数据是否可以用
    if check_data(x0) ==0:
        pass
    else:
        x0 = offset(x0)
    #计算AOG
    x0 = np.array(x0)
    x1 = np.cumsum(x0)
    #计算x1的均值生成序列
    x1 = pd.DataFrame(x1)
    z1 = (x1+x1.shift())/2.0#该项与该项的前一项相加除以2，用shift比循环代码更简单
    z1 = z1[1:].values.reshape((len(z1)-1,1))#再将刚刚算出的数据转成ndarray,删去nan
    B = np.append(-z1,np.ones_like(z1),axis=1)#合并数据形成B矩阵
    Y = x0[1:].reshape((len(x0)-1,1))#建立Y矩阵
    #计算参数a,b np.dot为点乘,np.linalg.inv为矩阵求逆
    [[a],[b]] = np.dot(np.dot((np.linalg.inv(np.dot(B.T,B))),B.T),Y)
    #方程求解 f(k+1)表示x1(k+1)
    f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2))
    #求出估计的所有x1的预测值,大小和x0一样
    x1_pre = [f(k) for k in range(1,len(x0)+1)]
    #求x0的预测值
    #x1_pre = pd.DataFrame(x1_pre)
   
    delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
    #检验预测值，利用残差检验
    residual_error = np.abs(x0-np.array(x1_pre))
    residual_error_max = residual_error.max
    #级比偏差值检验
    p = [1-((1-0.5*a)/(1+0.5*a))*l for l in lambda_k]


    return a,b,residual_error_max,p,f

6. 算出的结果和画出的图
   `
   结果预测出的结果：

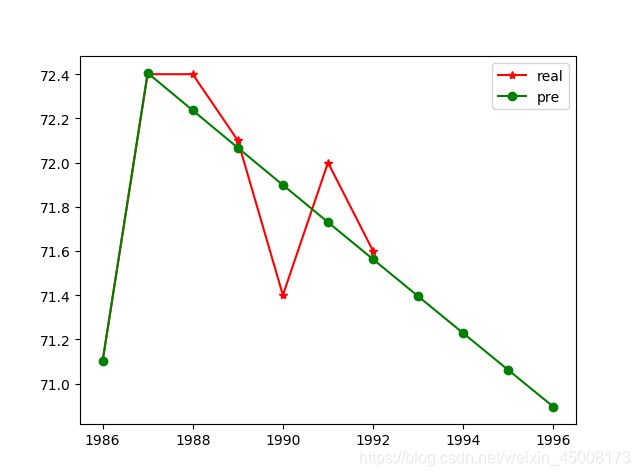
[71.1, 72.40574144043057, 72.23623656189375, 72.06712850138501, 
71.89841632994649, 71.73009912077032, 71.56217594925329, 
71.39464589292402, 71.22750803147937, 71.06076144678445, 
70.89440522284349]

由上述来看，这样预测是不够准确的，因为他都是线性变化的，所以我们可以使用2阶以上的来进行预测即GM(2,1)、DGM、Verhulst模型。

上述说的三种方法，基本思路都是一样的，在白化方程方面转化成了2阶方程具体方法可自行bing了解。python解常微分方程的教程博客

特别提出以下：
Verhulst模型经常用于描述饱和状态的过程，更适用于S型曲线。