【某航】A*算法实现十五数码问题--人工智能课程大作业

代码链接：github代码

1.问题要求

15数码问题是在4×4方格盘上，放有15个数码，剩下一个位置为空（方便起见，用0表示空），每一空格其上下左右的数码可移至空格。本问题给定初始位置和目标位置，要求通过一系列的数码移动，将初始状态转化为目标状态。
状态转换的规则：空格四周的数移向空格，我们可以看作是空格移动，它最多可以有4个方向的移动，即上、下、左、右。问题的求解方法，就是从给定的初始状态出发，不断地将空格上下左右的数码移至空格，将一个状态转化成其它状态，直到产生目标状态。
采用本章所学的A*算法程序实现十五数码问题。提交1篇实验报告，以及完整的软件系统和相关文档，包括源程序。

2.算法分析

A*算法分析：
在搜索的每一步都利用估价函数f(n)= g(n)+h(n)对Open表中的节点进行排序表中的节点进行排序, 找出一个最有希望的节点作为下一次扩展的节点。且满足条件：h(n)≤h*(n)。其中g(n) 是在状态空间中从初始状态到状态n的实际代价，h(n) 是从状态n到目标状态的最佳路径的估计代价。
算法过程如下：
读入初始状态和目标状态，并计算初始状态评价函数值f；
初始化两个open表和closed表，将初始状态放入open表中
如果open表为空，则查找失败；
否则：
① 在open表中找到评价值最小的节点，作为当前结点，并放入closed表中；
② 判断当前结点状态和目标状态是否一致，若一致，跳出循环；否则跳转到③；
③ 对当前结点，分别按照上、下、左、右方向移动空格位置来扩展新的状态结点，并计算新扩展结点的评价值f并记录其父节点；
④ 对于新扩展的状态结点，进行如下操作：
A．新节点既不在open表中，也不在closed表中，则添加进OPEN表；
B．新节点在open表中，则计算评价函数的值，取最小的。
C．新节点在closed表中，则计算评价函数的值，取最小的。
⑤ 把当前结点从open表中移除；

3.实验设计

根据A*算法具体原理，在Python3中进行代码编写。
（1）定义状态节点：
定义State类，初始化以下参数： deepth: 从初始节点到目前节点所经过的步数； rest_dis: 启发距离； state: 节点存储的状态 4*4的列表； hash_value: 哈希值，用于判重； father_node: 父节点指针。并且定义child: 孩子节点；fn: 评价函数的值。
在这其中，重点是对每一个节点计算其哈希值，保证节点不重复拓展，另外，根据fn评价函数的值通过heapq堆排序确定OPEN表中待拓展节点的顺序。
（2）A* 算法：
主要在A_star函数中进行，其中，start: 起始状态； end: 终止状态； distance_fn: 距离函数； generate_child_fn: 产生孩子节点的函数；并返回: 最优路径长度。在这其中主体是while循环，只要OPEN表不为空，就一直循环，如果找到目标节点，则直接输出路径，并且返回最优路径长度。
其中，采用heapq堆排序算法，对OPEN表中的节点进行自动排序，每次弹出OPEN表中评价函数值最低的节点，并且使用堆排序在每次插入新节点排序的时间复杂度都为 ，尽可能降低时间复杂度。
（3）生成子节点函数：
主要在generate_child函数中进行，参数中sn_node: 当前节点； sg_node: 最终状态节点； hash_set: 哈希表，用于判重； open_table: OPEN表； cal_distence: 距离函数。
对每一个节点，进行[‘up’, ‘down’, ‘left’, ‘right’]四个方向的移动，如果超过界限即x < 0 or x >= 4 or y < 0 or y >= 4，则略过此节点，没超过界限，进行相应移动元素位置互换，并通过hash值判断该状态是否已经扩展过，如果没有，则计算其哈希值并加入hash表，最后计算深度，启发值等建立新的节点node并加入heapq堆中。
（4）计算距离函数(启发函数h(n))：
默认采用曼哈顿距离的计算方法，计算每一个位置的数据与它理论位置的横纵标和与纵坐标距离之和。
另外还设计了欧氏距离的计算方法，即每一个位置的数据与它理论位置直线距离之和。
（5）计算评价函数(f(n))：
取f(n)=g(n)+h(n)=d(n)+P(n)。其中，d(n)为当前结点的深度，P(n)为计算距离函数，当前状态下各将牌到目标位置的距离之和。距离的计算公式：第一种：曼哈顿距离，即现在状态和目标状态之间，横坐标之差绝对值与纵坐标之差绝对值的和；第二种：欧氏距离，即现在的状态到目标状态的直线距离。P(n)越小，表示该节点越接近目标状态。

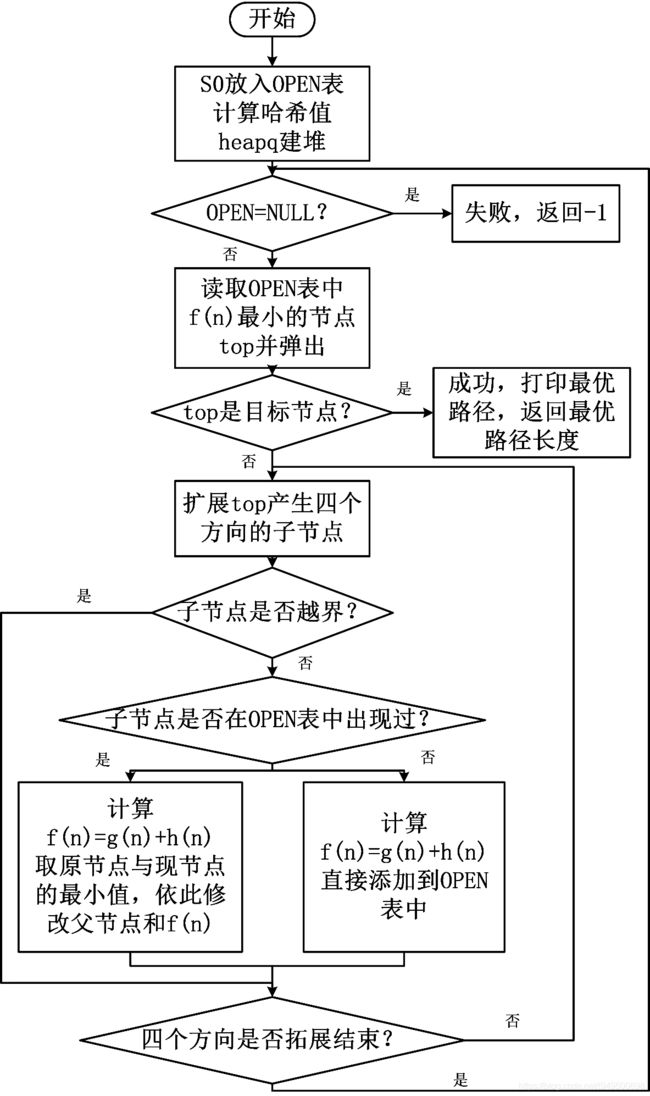
4.方法流程图

5.实验方案与运行结果分析

（1）不同距离函数对结果影响：
在本实验计算启发式函数的过程中，设计了两种距离函数的计算方法，分别是曼哈顿距离和欧氏距离。
通过运行代码，在项目文件夹中通过命令行输入：（代码见github代码）
python A_star.py -m cal_E_distence > report_A_star_E.txt
即可通过欧氏距离的计算方法计算启发函数，并且输出结果（包括搜索路径，最优路径长度，搜索时长，共检测节点数）保存在report_A_star_E.txt文件中。示例输出见：

report_A_star_E.txt文件： 最终搜索路径为：
------ 0 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 15, 10, 11]
[0, 14, 7, 12]
------ 1 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 15, 10, 11]
[14, 0, 7, 12]
------ 2 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 0, 10, 11]
[14, 15, 7, 12]
------ 3 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 0, 11]
[14, 15, 7, 12]
------ 4 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[14, 15, 0, 12]
------ 5 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[14, 0, 15, 12]
------ 6 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[13, 10, 7, 11]
[0, 14, 15, 12]
------ 7 --------
[5, 1, 2, 4]
[9, 6, 3, 8]
[0, 10, 7, 11]
[13, 14, 15, 12]
------ 8 --------
[5, 1, 2, 4]
[0, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
------ 9 --------
[0, 1, 2, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
------ 10 --------
[1, 0, 2, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
------ 11 --------
[1, 2, 0, 4]
[5, 6, 3, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
------ 12 --------
[1, 2, 3, 4]
[5, 6, 0, 8]
[9, 10, 7, 11]
[13, 14, 15, 12]
------ 13 --------
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 0, 11]
[13, 14, 15, 12]
------ 14 --------
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 0]
[13, 14, 15, 12]
------ 15 --------
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 12]
[13, 14, 15, 0]
采用欧式距离计算启发函数
搜索最优路径长度为 15
搜索时长为 0.07203030586242676 s
共检测节点数为 1127

同理，通过输入
python A_star.py -m cal_M_distence > report_A_star_M.txt
即可通过曼哈顿距离的计算方法计算启发函数，并且输出结果保存在report_A_star_M.txt文件中。
改变初始状态，用同样的方法测试，结果保存在report_A_star_E_new.txt和report_A_star_M_new.txt中，对比两种方法的结果。

	启发函数计算方法	搜索最优路径长度	搜索时长	共检测节点数
情况1	欧氏距离	15	0.0720s	1127
情况1	曼哈顿距离	21	0.1253s	2117
情况2	欧氏距离	43	337.8415s	3431727
情况2	曼哈顿距离	45	21.6971	361937

PS:每次运行结果会有稍许不同
情况1：
S0 = [[5, 1, 2, 4],
[9, 6, 3, 8],
[13, 15, 10, 11],
[0, 14, 7, 12]]
特点：较为简单，容易完成搜索
情况2：
S0 = [[11, 9, 4, 15],
[1, 3, 0, 12],
[7, 5, 8, 6],
[13, 2, 10, 14]]
（2）有界深度优先算法VS广度优先算法VS A*启发式搜索：
为了对比分析A*启发式搜索算法的优越性，另外编写了有界深度优先算法，广度优先算法进行算法的横向比较。
有界深度优先算法：DFS_max_deepth.py。在A_star.py的基础上进行修改，取消rest_dis 启发距离函数的计算，取消heapq的堆排序应用，直接设置OPEN表，每扩展一个节点，将该节点添加到OPEN表首部。另外，为了尽可能保证程序有解，在深度优先算法的基础上，添加了深度限制，即在扩展节点之前，计算当前节点的深度，如果深度大于规定的阈值，则不扩展该节点。
广度优先算法：BFS.py。在A_star.py的基础上修改，取消取消rest_dis 启发距离函数的计算，在 heapq的堆排序中，根据目前的深度deepth进行排序，即优先扩展同一层的节点，为广度优先算法的应用。
运行代码方法：
在项目文件夹中通过命令行输入：
python DFS_max_deepth.py > report_DFS_max_deepth.txt
即可通过有界深度优先算法，并且输出结果保存在report_DFS_max_deepth.txt文件中。
在项目文件夹中通过命令行输入：
python BFS.py > report_BFS.txt
即可通过广度优先算法，并且输出结果保存在report_BFS.txt文件中。

	启发函数计算方法	搜索最优路径长度	搜索时长	共检测节点数
情况1	有界深度优先(max_deepth=25)	23	62.7500s	1363348
情况1	广度优先	15	8.1250s	195811
情况1	A星(曼哈顿距离)	21	0.1253s	2117

通过对比分析，可以发现，A星算法的搜索时长和检测节点数明显小于另外两种方法，可见启发式信息对于搜索过程的重要性；另外，有界深度优先算法的算法性能差异较大，设置不同的最深深度得到的结果有一定的差异，一般设置较大会造成内存爆炸的现象，所以通过该方法进行搜索较为困难，对于任务较为复杂的情况，很难快速求解。另外，广度优先算法，针对较为简单问题，基本可以以最短路径给出答案，但同时搜索时间和搜索节点数一定会比启发式搜索多一些，针对复杂问题，很难给出答案，每扩展一层，都会以指数的形式增加待扩展节点的数量，很难得出答案。
综上所述，与深度优先和广度优先算法相比，启发式搜索算法有很强的优越性，一般情况下要尽可能去寻找启发函数，添加到代码中辅助进行算法的训练，尽可能缩短程序运行时间，提高程序效率。

代码链接：github代码
代码示例：

#-*-coding:utf-8-*-

import heapq
import copy
import time
import math
import argparse

# 初始状态
# S0 = [[11, 9, 4, 15],
#       [1, 3, 0, 12],
#       [7, 5, 8, 6],
#       [13, 2, 10, 14]]
S0 = [[5, 1, 2, 4],
      [9, 6, 3, 8],
      [13, 15, 10, 11],
      [0, 14, 7, 12]]

# 目标状态
SG = [[1, 2, 3, 4],
      [5, 6, 7, 8],
      [9, 10, 11, 12],
      [13, 14, 15, 0]]

# 上下左右四个方向移动
MOVE = {'up': [1, 0],
        'down': [-1, 0],
        'left': [0, -1],
        'right': [0, 1]}

# OPEN表
OPEN = []

# 节点的总数
SUM_NODE_NUM = 0

# 状态节点
class State(object):
    def __init__(self, deepth=0, rest_dis=0.0, state=None, hash_value=None, father_node=None):
        '''
        初始化
        :参数 deepth: 从初始节点到目前节点所经过的步数
        :参数 rest_dis: 启发距离
        :参数 state: 节点存储的状态 4*4的列表
        :参数 hash_value: 哈希值，用于判重
        :参数 father_node: 父节点指针
        '''
        self.deepth = deepth
        self.rest_dis = rest_dis
        self.fn = self.deepth + self.rest_dis
        self.child = []  # 孩子节点
        self.father_node = father_node  # 父节点
        self.state = state  # 局面状态
        self.hash_value = hash_value  # 哈希值

    def __lt__(self, other):  # 用于堆的比较，返回距离最小的
        return self.fn < other.fn

    def __eq__(self, other):  # 相等的判断
        return self.hash_value == other.hash_value

    def __ne__(self, other):  # 不等的判断
        return not self.__eq__(other)


def cal_M_distence(cur_state):
    '''
    计算曼哈顿距离
    :参数 state: 当前状态,4*4的列表, State.state
    :返回: M_cost 每一个节点计算后的曼哈顿距离总和
    '''
    M_cost = 0
    for i in range(4):
        for j in range(4):
            if cur_state[i][j] == SG[i][j]:
                continue
            num = cur_state[i][j]
            if num == 0:
                x, y = 3, 3
            else:
                x = num / 4  # 理论横坐标
                y = num - 4 * x - 1  # 理论的纵坐标
                M_cost += (abs(x - i) + abs(y - j))
    return M_cost

def cal_E_distence(cur_state):
    '''
    计算曼哈顿距离
    :参数 state: 当前状态,4*4的列表, State.state
    :返回: M_cost 每一个节点计算后的曼哈顿距离总和
    '''
    E_cost = 0
    for i in range(4):
        for j in range(4):
            if cur_state[i][j] == SG[i][j]:
                continue
            num = cur_state[i][j]
            if num == 0:
                x, y = 3, 3
            else:
                x = num / 4  # 理论横坐标
                y = num - 4 * x - 1  # 理论的纵坐标
                E_cost += math.sqrt((x - i)*(x - i) + (y - j)*(y - j))
    return E_cost

def generate_child(sn_node, sg_node, hash_set, open_table, cal_distence):
    '''
    生成子节点函数
    :参数 sn_node:  当前节点
    :参数 sg_node:  最终状态节点
    :参数 hash_set:  哈希表，用于判重
    :参数 open_table: OPEN表
    :参数 cal_distence: 距离函数
    :返回: None
    '''
    if sn_node == sg_node:
        heapq.heappush(open_table, sg_node)
        print('已找到终止状态！')
        return
    for i in range(0, 4):
        for j in range(0, 4):
            if sn_node.state[i][j] != 0:
                continue
            for d in ['up', 'down', 'left', 'right']:  # 四个偏移方向
                x = i + MOVE[d][0]
                y = j + MOVE[d][1]
                if x < 0 or x >= 4 or y < 0 or y >= 4:  # 越界了
                    continue
                state = copy.deepcopy(sn_node.state)  # 复制父节点的状态
                state[i][j], state[x][y] = state[x][y], state[i][j]  # 交换位置
                h = hash(str(state))  # 哈希时要先转换成字符串
                if h in hash_set:  # 重复了
                    continue
                hash_set.add(h)  # 加入哈希表

                # 记录扩展节点的个数
                global SUM_NODE_NUM
                SUM_NODE_NUM += 1

                deepth = sn_node.deepth + 1  # 已经走的距离函数
                rest_dis = cal_distence(state)  # 启发的距离函数
                node = State(deepth, rest_dis, state, h, sn_node)  # 新建节点
                sn_node.child.append(node)  # 加入到孩子队列
                heapq.heappush(open_table, node)  # 加入到堆中

                # show_block(state, deepth) # 打印每一步的搜索过程


def show_block(block, step):
    print("------", step, "--------")
    for b in block:
        print(b)

def print_path(node):
    '''
    输出路径
    :参数 node: 最终的节点
    :返回: None
    '''
    print("最终搜索路径为：")
    steps = node.deepth

    stack = []  # 模拟栈
    while node.father_node is not None:
        stack.append(node.state)
        node = node.father_node
    stack.append(node.state)
    step = 0
    while len(stack) != 0:
        t = stack.pop()
        show_block(t, step)
        step += 1
    return steps


def A_start(start, end, distance_fn, generate_child_fn):
    '''
    A*算法
    :参数 start: 起始状态
    :参数 end: 终止状态
    :参数 distance_fn: 距离函数，可以使用自定义的
    :参数 generate_child_fn: 产生孩子节点的函数
    :返回: 最优路径长度
    '''
    root = State(0, 0, start, hash(str(S0)), None)  # 根节点
    end_state = State(0, 0, end, hash(str(SG)), None)  # 最后的节点
    if root == end_state:
        print("start == end !")

    OPEN.append(root)
    heapq.heapify(OPEN)

    node_hash_set = set()  # 存储节点的哈希值
    node_hash_set.add(root.hash_value)
    while len(OPEN) != 0:
        top = heapq.heappop(OPEN)
        if top == end_state:  # 结束后直接输出路径
            return print_path(top)
        # 产生孩子节点，孩子节点加入OPEN表
        generate_child_fn(sn_node=top, sg_node=end_state, hash_set=node_hash_set,
                          open_table=OPEN, cal_distence=distance_fn)
    print("无搜索路径!")  # 没有路径
    return -1

if __name__ == '__main__':

    # 可配置式运行文件
    parser = argparse.ArgumentParser(description='选择距离计算方法')
    parser.add_argument('--method', '-m', help='method 选择距离计算方法(cal_E_distence or cal_M_distence)', default = 'cal_M_distence')
    args = parser.parse_args()
    method = args.method

    time1 = time.time()
    if method == 'cal_E_distence':
        length = A_start(S0, SG, cal_E_distence, generate_child)
    else:
        length = A_start(S0, SG, cal_M_distence, generate_child)
    time2 = time.time()
    if length != -1:
        if method == 'cal_E_distence':
            print("采用欧式距离计算启发函数")
        else:
            print("采用曼哈顿距离计算启发函数")
        print("搜索最优路径长度为", length)
        print("搜索时长为", (time2 - time1), "s")
        print("共检测节点数为", SUM_NODE_NUM)

如果感觉对你有所帮助，不妨点个赞，关注一波，激励博主持续更新！