Open3d 学习计划——9(ICP配准)
原文地址
Open3d 学习计划——9(ICP配准)
- ICP 配准
-
- 可视化帮助函数
- 输入
- 点对点 ICP
- 点对面ICP
ICP 配准
本教程演示了ICP(迭代最近点)配准算法。多年来,它一直是研究和工业中几何配准的主流。输入是两个点云和一个初始转换,该转换将源点云和目标点云大致对齐,输出是精确的变换,使两点云紧密对齐。辅助函数draw_registration_result在配准过程中进行可视化。在本教程中,我们演示了两种ICP变体,点对点(point-to-point)ICP和点对面(point-to-plane)ICP[Rusinkiewicz2001]。
可视化帮助函数
下面的函数将目标点云和源点云可视化,并通过对齐变换对其进行转换。目标点云和源点云分别用青色和黄色绘制。两点云重叠的越紧密,对齐的结果就越好。
def draw_registration_result(source, target, transformation):
source_temp = copy.deepcopy(source)
target_temp = copy.deepcopy(target)
source_temp.paint_uniform_color([1, 0.706, 0])
target_temp.paint_uniform_color([0, 0.651, 0.929])
source_temp.transform(transformation)
o3d.visualization.draw_geometries([source_temp, target_temp],
zoom=0.4459,
front=[0.9288, -0.2951, -0.2242],
lookat=[1.6784, 2.0612, 1.4451],
up=[-0.3402, -0.9189, -0.1996])
注意: 由于函数transformand paint_uniform_color会更改点云,我们调用copy.deepcoy进行复制并保护原始点云。
输入
下面的代码从两个文件中读取源点云和目标点云。给出了一个粗略的变换。
注意:初始对准通常通过全局配准算法来实现。有关示例,请参见全局配准。
source = o3d.io.read_point_cloud("../../TestData/ICP/cloud_bin_0.pcd")
target = o3d.io.read_point_cloud("../../TestData/ICP/cloud_bin_1.pcd")
threshold = 0.02
trans_init = np.asarray([[0.862, 0.011, -0.507, 0.5],
[-0.139, 0.967, -0.215, 0.7],
[0.487, 0.255, 0.835, -1.4],
[0.0, 0.0, 0.0, 1.0]])
draw_registration_result(source, target, trans_init)
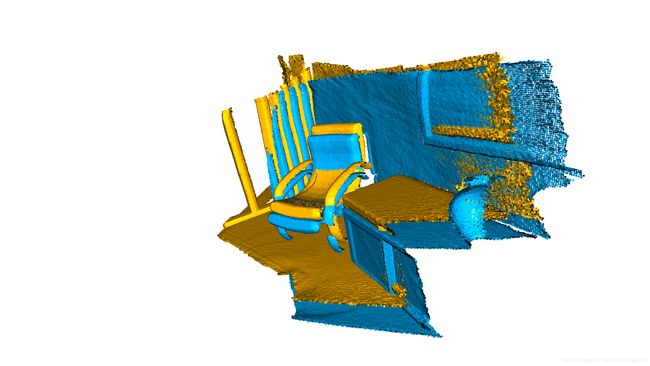
该函数evaluate_registration计算两个主要指标。fitness计算重叠区域(内点对应关系/目标点数)。越高越好。inlier_rmse计算所有内在对应关系的均方根误差RMSE。越低越好。
reg_p2p = o3d.registration.registration_icp(source, target, threshold, trans_init,
o3d.registration.TransformationEstimationPointToPoint(),
o3d.registration.ICPConvergenceCriteria(max_iteration = 2000))
print(reg_p2p)
print("Transformation is:")
print(reg_p2p.transformation)
draw_registration_result(source, target, reg_p2p.transformation)
registration::RegistrationResult with fitness=6.211230e-01, inlier_rmse=6.583448e-03, and correspondence_set size of 123501
Access transformation to get result.
Transformation is:
[[ 0.84024592 0.00687676 -0.54241281 0.6463702 ]
[-0.14819104 0.96517833 -0.21706206 0.81180074]
[ 0.52111439 0.26195134 0.81189372 -1.48346821]
[ 0. 0. 0. 1. ]]
点对点 ICP
一般来说,ICP算法迭代了两个步骤:
1.使用当前变换矩阵 T \ T T进行变换从源点云 P \ P P和目标点云 Q \ Q Q找到对应关系集 k \large k k={(p,q)}通过最小化在对应集 P \ P P上定义的目标函数 E ( T ) \ E(T) E(T)来更新变换 T \ T T。不同的ICP变体使用不同的目标函数 E ( T ) \ E(T) E(T)
[BeslAndMcKay1992][ChenAndMedioni1992][Park2017]。我们首先演示点对点ICP算法[BeslAndMcKay1992],使用目标函数:
E ( T ) = ∑ ( p , q ) ∈ k ∥ p − T q ∥ 2 E(T)=\sum_{(p,q)\in{k}} \|p-Tq\|^2 E(T)=(p,q)∈k∑∥p−Tq∥2
该类TransformationEstimationPointToPoint提供用于计算点对点ICP目标函数的残差和雅可比矩阵的函数。函数registration_icp将其作为参数并运行点对点ICP以获得结果。
print("Apply point-to-point ICP")
reg_p2p = o3d.registration.registration_icp(
source, target, threshold, trans_init,
o3d.registration.TransformationEstimationPointToPoint())
print(reg_p2p)
print("Transformation is:")
print(reg_p2p.transformation)
draw_registration_result(source, target, reg_p2p.transformation)
Apply point-to-point ICP registration::RegistrationResult with fitness=3.724495e-01, inlier_rmse=7.760179e-03, and correspondence_set size of 74056
Access transformation to get result. Transformation is:
[[ 0.83924644 0.01006041 -0.54390867 0.64639961]
[-0.15102344 0.96521988 -0.21491604 0.75166079]
[ 0.52191123 0.2616952 0.81146378 -1.50303533]
[ 0. 0. 0. 1. ]]
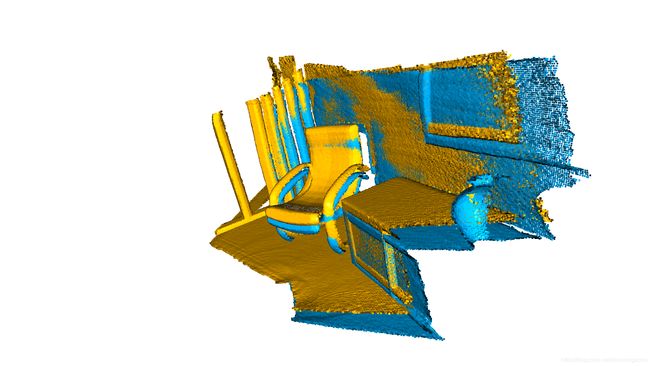
fitness得分从0.174723增加到0.372450。inlier_rmse从0.011771减少到0.007760。默认情况下,registration_icp运行直到收敛或达到最大迭代次数(默认为30)。可以更改它以允许更多的计算时间并进一步改善结果。
reg_p2p = o3d.registration.registration_icp(source, target, threshold, trans_init,
o3d.registration.TransformationEstimationPointToPoint(),
o3d.registration.ICPConvergenceCriteria(max_iteration = 2000))
print(reg_p2p)
print("Transformation is:")
print(reg_p2p.transformation)
draw_registration_result(source, target, reg_p2p.transformation)
registration::RegistrationResult with fitness=6.211230e-01, inlier_rmse=6.583448e-03, and correspondence_set size of 123501
Access transformation to get result.
Transformation is:
[[ 0.84024592 0.00687676 -0.54241281 0.6463702 ]
[-0.14819104 0.96517833 -0.21706206 0.81180074]
[ 0.52111439 0.26195134 0.81189372 -1.48346821]
[ 0. 0. 0. 1. ]]
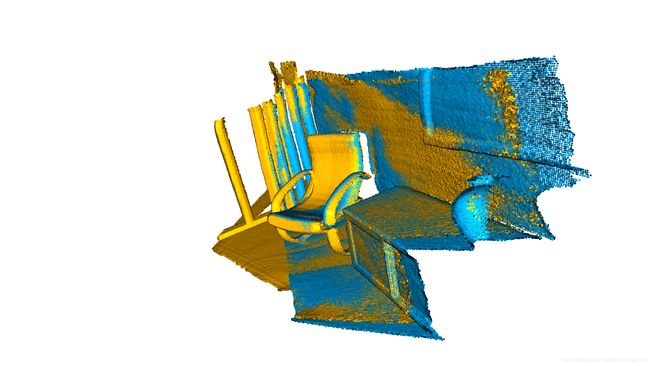
最终的对齐是紧密的。fitness分数提高到0.621123。inlier_rmse降低到0.006583。
点对面ICP
点对面 ICP算法[ChenAndMedioni1992]使用了不同的目标函数
E ( T ) = ∑ p , q ∈ k ( ( p − T q ) ⋅ n p ) 2 , E(T)=\sum_{p,q\in{k}} \left(\left(p-Tq\right)\cdot{n_{p}}\right)^2, E(T)=p,q∈k∑((p−Tq)⋅np)2,
这里 n p n_{p} np是点云p的法向量。[Rusinkiewicz2001] 已经表明,点对面 ICP算法比点对点ICP算法具有更快的收敛速度。
registration_icp用不同的参数调用TransformationEstimationPointToPlane。在内部,该类实现函数以计算点对面ICP目标函数的残差和雅可比矩阵。
print("Apply point-to-plane ICP")
reg_p2l = o3d.registration.registration_icp(
source, target, threshold, trans_init,
o3d.registration.TransformationEstimationPointToPlane())
print(reg_p2l)
print("Transformation is:")
print(reg_p2l.transformation)
draw_registration_result(source, target, reg_p2l.transformation)
Apply point-to-plane ICP
registration::RegistrationResult with fitness=6.209722e-01, inlier_rmse=6.581453e-03, and correspondence_set size of 123471
Access transformation to get result.
Transformation is:
[[ 0.84023324 0.00618369 -0.54244126 0.64720943]
[-0.14752342 0.96523919 -0.21724508 0.81018928]
[ 0.52132423 0.26174429 0.81182576 -1.48366001]
[ 0. 0. 0. 1. ]]
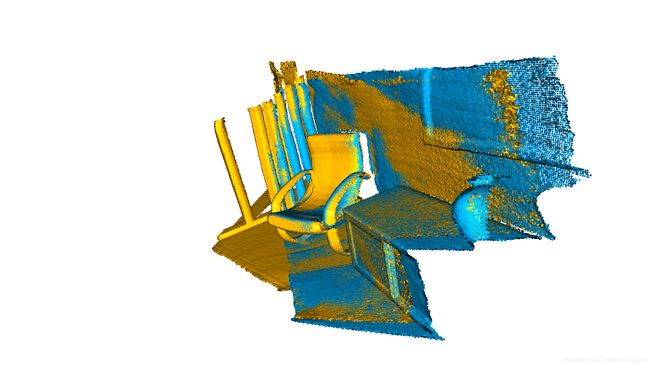
点到面ICP在30次迭代(fitness0.620972和inlier_rmse0.006581)中达到紧密对齐。
点对面ICP算法使用点法线。在本教程中,我们从文件加载法线。如果未给出法线,则可以使用顶点法线估计来计算它们。