初始化、正则化调试(基于简单Linear,pytorch)
一.权重初始化(正态分布可以加速学习):
初始化权重,使其数据保持标准差在1左右以防止梯度消失或者爆炸,在卷积神经网络中常用,pytorch直接默认了

自定义初始化权重
import torch.nn as nn
import torch
class Network(nn.Module):
def __init__(self):
super().__init__()
self.Conv2d = nn.Conv2d(3, 10)
self.bn = nn.BatchNorm2d(10)
self.relu = nn.ReLU()
self._init_weight() # 在初始化网络时, 会执行该函数,然后初始化网络中的每个module
def forward(self, x):
x = self.Conv2d(x)
x = self.bn(x)
return self.relu(x)
def _init_weight(self):
for m in self.modules(): # 继承nn.Module的方法
if isinstance(m, nn.Conv2d):
torch.nn.init.kaiming_normal_(m.weight)
elif isinstance(m, nn.BatchNorm2d):
m.weight.data.fill_(1)
m.bias.data.zero_()
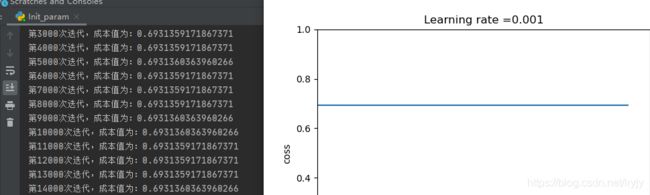
1.权重为常数
# 网络 LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
class Tnet(torch.nn.Module):
def __init__(self, input, output):
super(Tnet, self).__init__()
self.tnet = torch.nn.Sequential(torch.nn.Linear(input, 10),
torch.nn.ReLU(True),
torch.nn.Linear(10, 5),
torch.nn.ReLU(True),
torch.nn.Linear(5, output),
)
for i in range(0, 5, 2):
torch.nn.init.constant_(self.tnet[i].weight, 0)
torch.nn.init.constant_(self.tnet[i].bias, 0)
def forward(self, x):
x = self.tnet(x)
return x
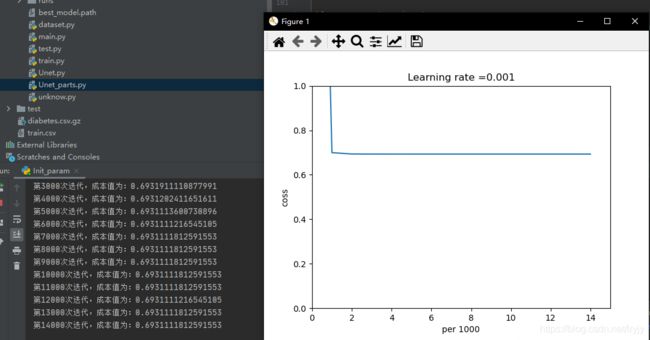
2.均匀分布
for i in range(0, 5, 2):
torch.nn.init.uniform_(self.tnet[i].weight, a=0,b =1)
torch.nn.init.uniform_(self.tnet[i].bias, a=0, b=1)
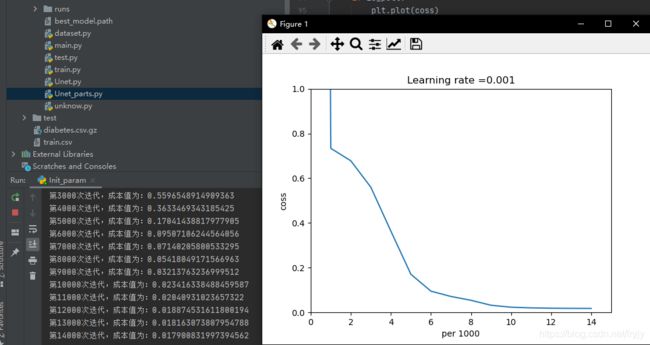
3.正态分布和抑梯度异常(默认)
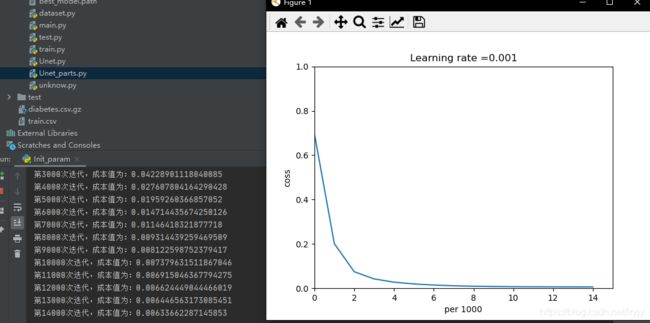
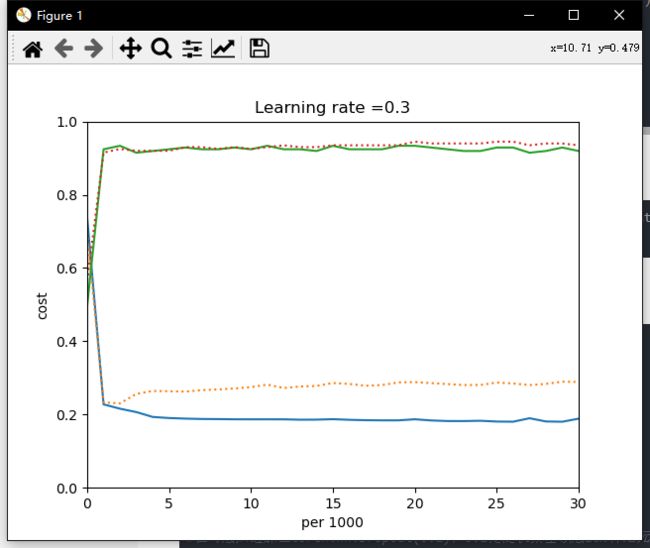
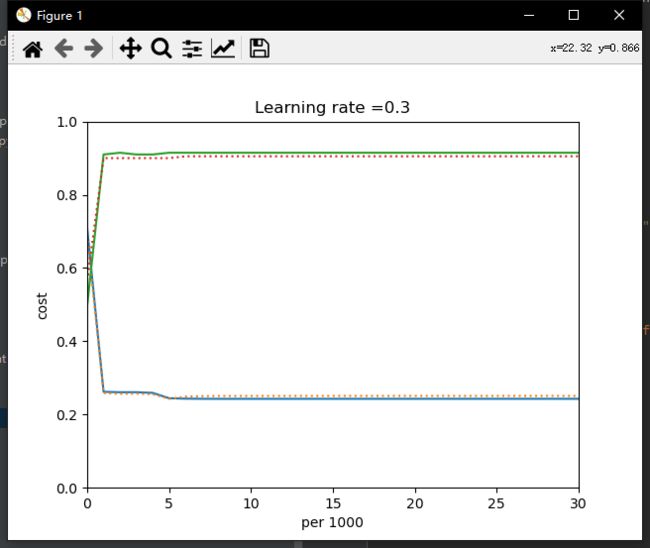
在本次数据集下可以看出正态分布效果更好,但是不同数据集权重初始化导致的训练结果影响也很大,后面讨论
二.正则化:
1.正则化
意义以及功能:当训练集以及测试集差距过大时,处理过拟合的一种方法
整个实验的代码:
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import scipy.io as sio
'''不使用正则化
使用正则化
2.1 使用L2正则化
2.2 使用随机节点删除'''
# 数据集
data = sio.loadmat('data.mat')
train_X = torch.from_numpy(data['X'])
train_Y = torch.from_numpy(data['y'])
# print(train_X.shape,train_Y.shape) torch.Size([211, 2]) torch.Size([211, 1])
test_X = torch.from_numpy(data['Xval'])
test_Y = torch.from_numpy(data['yval'])
# 网络 LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
class Tnet(torch.nn.Module):
def __init__(self, input, output):
super(Tnet, self).__init__()
self.tnet = torch.nn.Sequential(torch.nn.Linear(input, 20),
torch.nn.ReLU(True),
torch.nn.Linear(20, 5),
torch.nn.ReLU(True),
torch.nn.Linear(5, output),
)
def forward(self, x):
x = self.tnet(x)
return x
def predict(x, y, net):
pred = net(x)
pred = pred.cpu()
y = y.numpy().reshape(1, -1)
pred = pred.detach().numpy().reshape(1, -1)
m = pred.shape[1]
p = np.full((1,m),0)
for i in range(0, m):
if pred[0, i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
return np.mean((p[0,:] == y[0,:]))
# print("Accuracy: " + str(np.mean((p[0,:] == y[0,:]))))
def train(net, device, epoch=30001, lr=0.3, is_polt=True):
train_data = train_X.to(device=device, dtype=torch.float32)
label = train_Y.to(device=device, dtype=torch.float32)
Test_X = test_X.to(device=device, dtype=torch.float32)
Test_Y = test_Y.to(device=device, dtype=torch.float32)
# optimizer = torch.optim.Adam(net.parameters(),lr=lr)
optimizer = torch.optim.SGD(net.parameters(), lr=lr,momentum=0.9)
criterion = torch.nn.BCEWithLogitsLoss()
cost = []
t_cost = []
train_acc = []
test_acc = []
for i in range(epoch):
optimizer.zero_grad()
pred = net(train_data)
loss = criterion(pred, label)
loss.backward()
optimizer.step()
# test
t_pred = net(Test_X)
t_loss = criterion(t_pred, Test_Y)
t_loss = t_loss.item()
# train
loss = loss.item()
if i % 1000 == 0:
cost.append(loss)
t_cost.append(t_loss)
train_acc.append(predict(train_data, train_Y, net))
test_acc.append(predict(Test_X, test_Y, net))
if i % 10000 == 0:
print("第" + str(i) + "次迭代,成本值为:" + str(loss))
print('train')
print(predict(train_data, train_Y, net))
print('test')
print(predict(Test_X, test_Y, net))
# 绘制学习图
if is_polt:
plt.plot(range(len(cost)), cost, range(len(t_cost)), t_cost, ':',range(len(train_acc)),train_acc,range(len(test_acc)),test_acc,':')
plt.axis([0, 30, 0, 1])
plt.ylabel('cost')
plt.xlabel('per 1000')
plt.title("Learning rate =" + str(lr))
plt.show()
if __name__ == '__main__':
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
net = Tnet(2, 1)
net.to(device)
print('start')
train(net, device=device)
L2:
optimizer = torch.optim.Adam(model.parameters(), lr=learn_rate,weight_decay=0.01)
#这里的weight_decay=0.01相当于λ参数。
Dropout:0.05,在较小的网络中并不好用
model=torch.nn.Sequential(
torch.nn.Linear(in_put,Hidden1,bias=True),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(Hidden1,Hidden2,bias=True),
torch.nn.ReLU(),
torch.nn.Dropout(0.2),
torch.nn.Linear(Hidden2,out_put,bias=True),
#在每层后边加上torch.nn.Dropout(0.2),0.2是随机架空该层20%神经元。

再加上weight_decay=0.001

总结:L2正则化采用w二范数,更新权重时进行了权重的衰减,从而减小了正则化但是权重的衰减会使学习速度变慢
Dropout在这个网络中没有很好体验出来,随机性强会使权重震荡大
2.Momentum(指数加权平均)
提示:可能是样本数太少,虽然测试集的损失变大但是精度确越来越高,但是对于训练集可以明显看出加速了学习