图注意力网络GRAPH ATTENTION NETWORKS(gat)浅读
论文结构
- 摘要
- GAT结构
-
- 图注意层结构
摘要
我们提出了图注意力网络(GAT),是在图结构化数据上运行的新型神经网络体系结构,利用蒙版的自我注意层来解决基于图卷积或其近似的现有方法的缺点。通过堆叠节点能够参与其邻域特征的图层,我们(隐式)启用了对邻域中不同节点的不同权重的指定,而无需进行任何昂贵的矩阵运算(如反演)或依赖于了解图前期结构。通过这种方式,我们可以同时解决基于频谱的图神经网络的几个关键挑战,并使我们的模型易于适用于归纳和传导问题。我们的GAT模型已在四个已建立的转导图和归纳图基准测试中达到或匹配了最新技术成果:Cora,Citeseer和Pubmed引用网络数据集,以及蛋白质-蛋白质相互作用数据集(其中在训练期间看不见测试图)。
GAT结构
本节介绍了一种通过层叠(stacking)方式可以用于构建任意图注意力网络的层块(block layer),并且描述了它和之前的图处理在理论和实际应用的优点以及限制。
图注意层结构
一个图注意层的输入是一组结点的特征值,即 h = { h ⃗ 1 , h ⃗ 2 , . . . , h ⃗ N } , h ⃗ i ∈ R F \mathbf{h}=\{\vec{h}_1,\vec{h}_2,...,\vec{h}_N\},\vec{h}_i\in\mathbb{R}^F h={h1,h2,...,hN},hi∈RF,其中 N N N为结点的个数, F F F是结点特征的个数。
一个图注意层的输出是其产生的一组新的结点特征值,即 h ′ = { h ⃗ 1 ′ , h ⃗ 2 ′ , . . . , h ⃗ N ′ } , h ⃗ i ′ ∈ R F ′ \mathbf{h}^\prime=\{\vec{h}^\prime_1,\vec{h}^\prime_2,...,\vec{h}^\prime_N\},\vec{h}^\prime_i\in\mathbb{R}^{F^\prime} h′={h1′,h2′,...,hN′},hi′∈RF′,其中 F ′ F^\prime F′通常比 F F F更大。
为了得到充足的信息以将输入特征转化为高维特征,则至少需要一个可学习的线性变换。所以一个共享的权重矩阵 W ∈ R F ′ × F W\in\mathbb{R}^{F^\prime\times F} W∈RF′×F将作用于每个结点,即 W h ⃗ i W\vec{h}_i Whi。然后对所有结点使用一个共享的注意力机制 a a a来计算两两结点间的注意力系数,即 e i j e_{ij} eij
e i j = a ( W h ⃗ i , W h ⃗ j ) e_{ij}=a(W\vec{h}_i,W\vec{h}_j) eij=a(Whi,Whj)
以上公式描述了结点 j j j的特征对结点 i i i的重要性。
在大多数的形式中,模型允许每个结点对其他所有结点计算注意力系数,借此得到所有结构化的信息。
在本论文中,我们只使用结点 i i i的第一层邻接结点(包括结点 i i i)记为 N i \mathcal{N}_i Ni来计算 e i j e_{ij} eij,并且为了便于不同结点之间的比较,需要用softmax函数对所有 e i j e_{ij} eij进行归一化,如下所示:
α i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) \alpha_{ij}=softmax_j(e_{ij})=\frac{exp(e_{ij})}{\sum_{k\in\mathcal{N}_i}exp(e_{ik})} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)
在本次实验中,我们将 a a a设置为一个单层的神经网络,其内部的权重参数为 a ⃗ ∈ R 2 F ′ \vec{a}\in \mathbb{R}^{2F\prime} a∈R2F′,并且使用 α = 0.2 \alpha=0.2 α=0.2的LeakyRelu作为激活函数,将以上式子全部带入后,得到注意力系数 α i j \alpha_{ij} αij的过程如下公式所示:
α i j = e x p ( L e a k y R e l u ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ j ] ) ) ∑ k ∈ N i e x p ( L e a k y R e l u ( a ⃗ T [ W h ⃗ i ∣ ∣ W h ⃗ j ] ) ) \alpha_{ij}=\frac{exp(LeakyRelu(\vec{a}^T[W\vec{h}_i||W\vec{h}_j]))}{\sum_{k\in \mathcal{N}_i}exp(LeakyRelu(\vec{a}^T[W\vec{h}_i||W\vec{h}_j]))} αij=∑k∈Niexp(LeakyRelu(aT[Whi∣∣Whj]))exp(LeakyRelu(aT[Whi∣∣Whj]))
其中 . T .^T .T表示转置, ∣ ∣ || ∣∣表示级联操作。
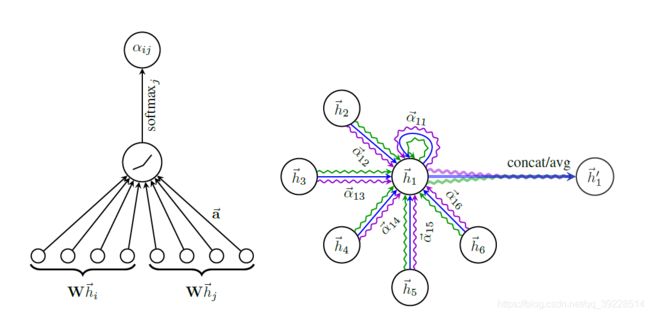
图1:左图表示 a ( W h ⃗ i ′ , W h ⃗ j ′ ) a(W\vec{h}_i^\prime,W\vec{h}_j^\prime) a(Whi′,Whj′)的过程,右图表示多端注意机制(K=3)时结点1的新特征值向量 h ⃗ 1 ′ \vec{h}_1^\prime h1′计算过程。不同颜色的线条表示独立的注意力计算,最后的输出 h ⃗ 1 ′ \vec{h}_1^\prime h1′可以由级联或者平均三个计算结果得到。
得到所有的注意力系数之后, h ⃗ i ′ \vec{h}_i^\prime hi′就能计算了:
h i ′ ⃗ = σ ( ∑ j ∈ N i α i j W h ⃗ j ) . \vec{h_i^\prime}=\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}W\vec{h}_j). hi′=σ(j∈Ni∑αijWhj).
其中 σ \sigma σ是一个非线性函数。
不过为了学习过程和结果的稳定性,论文使用了三个(k=3)独立的注意力机制对每一个结点求以上公式的结果,然后将所有结果平均起来得到最终的 h ⃗ i ′ \vec{h}_i^\prime hi′,即如下公式:
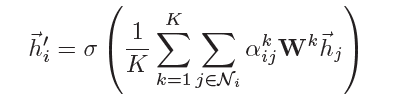
我目前对此论文的认知就是这个网络只是将一个图结构中每个结点 h ⃗ i \vec{h}_i hi的特征向量转化为更高维且更具有代表性的新向量 h ⃗ i ′ \vec{h}_i^\prime hi′。
即得到结点的新表示。
基于图的推荐系统以项目和用户为节点。通过利用项目与项目、用户与用户、用户与项目之间的关系以及内容信息,基于图的推荐系统能够生成高质量的推荐。推荐系统的关键是评价一个项目对用户的重要性。因此,可以将其转换为一个链路预测问题。目标是预测用户和项目之间丢失的链接。为了解决这个问题,有学者提出了一种基于GCN的图形自动编码器。还有学者结合GCN和RNN,来学习用户对项目评分的隐藏步骤。