Fast Fourier Convolution

Fast Fourier Convolution

背景：

感受野的概念： 卷积神经网络每一层输出的特征图（feature map）上的像素点映射回输入图像上的区域大小

例如：

扩大感受野的方法：非局部神经网络、膨胀卷积或可变形卷积

非局部神经网络：为了确定某个位置的新值，它计算该位置与所有其他位置的相似性得分，然后对所有位置的特征进行加权平均。

其中i为输入位置，j为所有搜索的位置

缺点：低效率

膨胀卷积或可变形卷积：本质上还是局部的，需要堆叠很多层才能获得大感受野

缺点：深度网络优化更困难、容易产生伪影。

创新点：

提出了一个新的卷积模块，fast Fourier convolution(FFC) ，不仅有非局部的感受野，而且在卷积内部就做了跨尺度信息的融合。

FFC构架：

FFC由两条相互连接的路径组成：一条在部分输入特征信道上进行普通卷积的空间（局部）路径，以及一条在频谱域中工作的频谱（全局）路径。每条路径都可以捕获具有不同感受野的互补信息。

Fourier Unit(FU)

性质1：对实信号应用二维FFT时，会产生完全对称的厄米特矩阵，对厄米特矩阵应用逆FFT时矩阵只有实元素。当用实张量进行FFT变换时，其结果是共轭对称的。因此，在不损失有用信息的情况下，我们可以只保留一半的结果，并通过使用共轭对称简单地恢复另一半。

性质2：傅里叶理论中的频谱卷积定理：更新频谱域中的单个值会影响空间域中全局的特征。

对于频谱变换器来说，大的核尺寸是不必要的，因为在频谱域中的任何操作都具有全局感受野。

Local Fourier Unit(LFU)

目的是捕捉半全局信息，做法是将input feature map分为4个patch，分别使用FU即可。

与FU相比，LFU需要更高的计算复杂度，这主要是由于增加了信道。LFU的效果因具体任务而异

复杂性分析：

FFC与普通卷积相比，计算成本相当，但当普通卷积使用大核卷积时，FFC体现了优越性，在频谱转换器时仍然使用1×1的核来学习全局感受野。

总结：提出了一种新的卷积算子，称为FFC。它利用傅里叶光谱理论在深度模型中实现非局部感受野。所提出的算子也经过设计以实现跨尺度融合。在三个具有代表性的计算机视觉任务上的综合实验证明FFC的有效性。

应用到图像修复当中

            Resolution-robust Large Mask Inpainting with Fourier Convolutions

背景：

针对问题：复杂几何结构的高分辨率图像缺失较大时修复效果不好。

作者认为：主要原因之一是修复网络和损失函数都缺乏有效感受野。

创新点：

1、提出了基于快速傅里叶卷积(FFC)的修复网络，可以在网络比较浅的层就有覆盖图像的感受野

2、应用了具有高感受野的语义分割网络的感知loss

3、引入了一种训练掩码生成的策略，可以生成多样性的Mask。

方法：

      问题定义：

在大掩模修复中，需要充分的考虑全局的上下文信息。因此一个好的架构需要在网络比较浅的地方就能够有较宽的感受野，对于宽掩模，特定位置的生成器的整个感受野可能在掩模内部，因此仅观察丢失的像素。对于高分辨率图像，这个问题变得尤为突出，不太适用。

快速傅里叶卷积(FFC)：FFC是可以在浅层中使用全局上下文的算子，FFC基于通道级别的FFT，并且有覆盖整个图像的感受野。

FFC设计上在通道级别分为两个分支：使用传统卷积的局部分支和使用FFT获取全局上下文信息的全局分支。

在重复结构上的修复示例

FFC可以在网络的浅层就开始考虑全局上下文信息，对于高分辨率图像来说十分有用。同时FFC非常适合捕获周期性的结构

Loss的设计：

原始的监督损失要求生成器尽可能地去还原 Ground Truth。但是当遮挡区域很大时，已有的可见区域的信息不足以还原，因此模型会做出很多模棱两可的判断，从而导致模糊。

利用一个预训练模型来评估预测图和目标图之间的距离。因为针对large mask 的修复问题的重点是理解图像的全局结构，因此不需要精确的还原，允许有一定的变化。

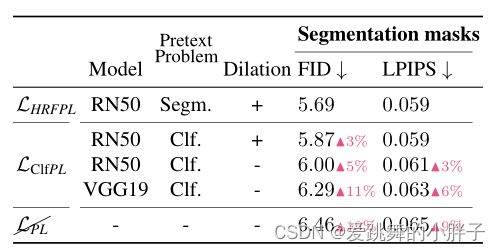
预训练模型的选取也很重要，分割模型会关注图像的高级语义信息，而分类模型可能会更关注图像的纹理。

大掩膜训练：

• 实验结果：超过了以往的 SOTA 模型，鲁棒性更好，扩展到高分辨率图像同样适用，且参数量和时间也更少。

存在不足：

1、对于变形的周期信号复原结果不佳。

2、在透视与复杂背景上表现不好