NNDL 作业8:RNN - 简单循环网络
1. 使用Numpy实现SRN
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t)
in_h2 = np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t)
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')2. 在1的基础上,增加激活函数tanh
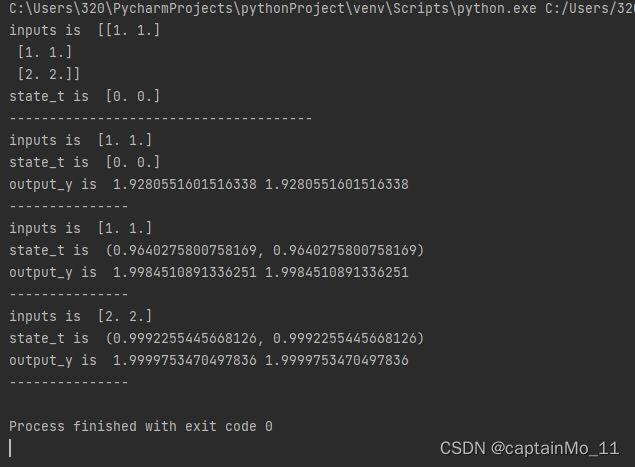
![]()
import numpy as np
inputs = np.array([[1., 1.],
[1., 1.],
[2., 2.]]) # 初始化输入序列
print('inputs is ', inputs)
state_t = np.zeros(2, ) # 初始化存储器
print('state_t is ', state_t)
w1, w2, w3, w4, w5, w6, w7, w8 = 1., 1., 1., 1., 1., 1., 1., 1.
U1, U2, U3, U4 = 1., 1., 1., 1.
print('--------------------------------------')
for input_t in inputs:
print('inputs is ', input_t)
print('state_t is ', state_t)
in_h1 = np.tanh(np.dot([w1, w3], input_t) + np.dot([U2, U4], state_t))
in_h2 = np.tanh(np.dot([w2, w4], input_t) + np.dot([U1, U3], state_t))
state_t = in_h1, in_h2
output_y1 = np.dot([w5, w7], [in_h1, in_h2])
output_y2 = np.dot([w6, w8], [in_h1, in_h2])
print('output_y is ', output_y1, output_y2)
print('---------------')3. 分别使用nn.RNNCell、nn.RNN实现SRN
import torch
batch_size = 1
seq_len = 3 # 序列长度
input_size = 2 # 输入序列维度
hidden_size = 2 # 隐藏层维度
output_size = 2 # 输出层维度
# RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
# 初始化参数 https://zhuanlan.zhihu.com/p/342012463
for name, param in cell.named_parameters():
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
seq = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(batch_size, hidden_size)
output = torch.zeros(batch_size, output_size)
for idx, input in enumerate(seq):
print('=' * 20, idx, '=' * 20)
print('Input :', input)
print('hidden :', hidden)
hidden = cell(input, hidden)
output = liner(hidden)
print('output :', output)import torch
batch_size = 1
seq_len = 3
input_size = 2
hidden_size = 2
num_layers = 1
output_size = 2
cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)
for name, param in cell.named_parameters(): # 初始化参数
if name.startswith("weight"):
torch.nn.init.ones_(param)
else:
torch.nn.init.zeros_(param)
# 线性层
liner = torch.nn.Linear(hidden_size, output_size)
liner.weight.data = torch.Tensor([[1, 1], [1, 1]])
liner.bias.data = torch.Tensor([0.0])
inputs = torch.Tensor([[[1, 1]],
[[1, 1]],
[[2, 2]]])
hidden = torch.zeros(num_layers, batch_size, hidden_size)
out, hidden = cell(inputs, hidden)
print('Input :', inputs[0])
print('hidden:', 0, 0)
print('Output:', liner(out[0]))
print('--------------------------------------')
print('Input :', inputs[1])
print('hidden:', out[0])
print('Output:', liner(out[1]))
print('--------------------------------------')
print('Input :', inputs[2])
print('hidden:', out[1])
print('Output:', liner(out[2]))4. 分析“二进制加法” 源代码(选做)
![]()
![]()
二进制加法思想为逢二进一,对应到代码上“二进制加法”主要做的事就是告诉RNN前一阶段的运算结果(进位)和当前阶段(加法),让RNN网络自己去学习加法和进位操作,具体操作就是将两个二进制传入,从最后一位开始,一层一层地通过sigmoid函数,得到最终的预测值。然后将预测值与准确值之间的差值设为layer_2层的loss值。得出loss值后,就可以得到对应层的权重参数,进而从最高位像前进行反向传播(从代码上来看,就是很普通的反向传播)。
动态演示:![]()
前向传播:
![]()
反向传播(黑色是预测值,errors是亮黄色,派生物(导数)是芥末色):
![]()
5. 实现“Character-Level Language Models”源代码(必做)
![]()
import torch
# 使用RNN 有嵌入层和线性层
num_class = 4 # 4个类别
input_size = 4 # 输入维度是4
hidden_size = 8 # 隐层是8个维度
embedding_size = 10 # 嵌入到10维空间
batch_size = 1
num_layers = 2 # 两层的RNN
seq_len = 5 # 序列长度是5
# 准备数据
idx2char = ['e', 'h', 'l', 'o'] # 字典
x_data = [[1, 0, 2, 2, 3]] # hello 维度(batch,seqlen)
y_data = [3, 1, 2, 3, 2] # ohlol 维度 (batch*seqlen)
inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)
# 构造模型
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.emb = torch.nn.Embedding(input_size, embedding_size)
self.rnn = torch.nn.RNN(input_size=embedding_size, hidden_size=hidden_size, num_layers=num_layers,
batch_first=True)
self.fc = torch.nn.Linear(hidden_size, num_class)
def forward(self, x):
hidden = torch.zeros(num_layers, x.size(0), hidden_size)
x = self.emb(x) # (batch,seqlen,embeddingsize)
x, _ = self.rnn(x, hidden)
x = self.fc(x)
return x.view(-1, num_class) # 转变维2维矩阵,seq*batchsize*numclass -》((seq*batchsize),numclass)
model = Model()
# 损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.05) # lr = 0.01学习的太慢
# 训练
for epoch in range(15):
optimizer.zero_grad()
outputs = model(inputs) # inputs是(seq,Batchsize,Inputsize) outputs是(seq,Batchsize,Hiddensize)
loss = criterion(outputs, labels) # labels是(seq,batchsize,1)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print("Predicted:", ''.join([idx2char[x] for x in idx]), end='')
print(",Epoch {}/15 loss={:.3f}".format(epoch + 1, loss.item()))
6. 分析“序列到序列”源代码(选做)
![]()
![]()
模型主要由两个部分组成,一个编码器(encoder)和一个解码器(decoder)。
通信领域,编码器(Encoder)指的是将信号进行编制,转换成容易传输的形式。
而在这里,主要指的是将句子编码成一个能够映射出句子大致内容的固定长度的向量。
如图4,对于投入到的每个RNN展开的节点,我们将会得到一个输出层输出和一个隐含层输出,我们最终需要使用到的是最后一个输入节点的隐含层输出。这里面最后一个隐含节点的输出蕴含了前面所有节点的输入内容。
解码器(Decoder),这里就是将由编码器得到的固定长度的向量再还原成对应的序列数据,一般使用和编码器同样的结构,也是一个RNN类的网络。
实际操作过程会将由编码器得到的定长向量传递给解码器,解码器节点会使用这个向量作为隐藏层输入和一个开始标志位作为当前位置的输入。得到的输出向量能够映射成为我们想要的输出结果,并且会将映射输出的向量传递给下一个展开的RNN节点。
每一次展开,会使用上一个节点的映射输出所对应的向量来投入到下一个输入中去,直到遇到停止标志位,即停止展开。
编码器的输入:
序列任务的数据集主要分为原序列和转换序列,比如说对话任务中,编码器的LSTM投入的输入为 are you free tomorrow四个词所对应的向量,而对起始的隐含层输入不做具体要求。
解码器的输入:
解码器的第一个输入节点位置为开始的标志位,如图5的
而后面跟进的输入在训练阶段一般有两种选择。一种是投入正确输出的输入。也被称为teacher force输入,即每一个节点的输入都为上一个节点正确的输出。
以下图6为例,我们需要的正确输出为W X Y Z,那么我们不论实际输出为多少,我们都将输入W X Y Z。
图6 teacher force训练模式
在这种情况进行训练,可以避免前面一个节点出错导致后面连续累计错误。并且在早期,使用这种方式训练,能够使训练更容易。
然而,在实际生成测试的过程中,我们不可能知道正确的数据是什么,因而难以避免这种错误累计的情况。所以产生了按照上一个节点输出作为下一个节点输出的训练情况。上面的图5就是表达的这种情况,这也是真正实际生成的方式。我们往往会在训练的后期加入这种投入的方式。结合二者进行训练,这样可以使得生成的效果更好。
解码器的输出:
对于输出部分没有什么特殊的,一般会将RNN节点所对应的输出通过一个全连接神经映射到字典维度大小的向量。再通过交叉熵来量化生成的分布和实际分布之间的差异,通过反向传播进而训练整个网络。
总结:
序列到序列模型看似非常完美,但是实际使用的过程中仍然会遇到一些问题。比如说句子长度过长,会产生梯度消失的问题。由于使用的是最后的一个隐含层输出的定长向量,那么对于远靠近末端的单词,“记忆”得会越深刻,而远远离的单词则会被逐渐稀释掉。面对这些问题,也有对应的一些解决方案比如加入attention,将句子倒向输入等。关于attention等内容将会在后面的文章进行介绍。
7. “编码器-解码器”的简单实现(必做)
![]()
import torch
import numpy as np
import torch.nn as nn
import torch.utils.data as Data
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
letter = [c for c in 'SE?abcdefghijklmnopqrstuvwxyz']
letter2idx = {n: i for i, n in enumerate(letter)}
seq_data = [['man', 'women'], ['black', 'white'], ['king', 'queen'], ['girl', 'boy'], ['up', 'down'], ['high', 'low']]
# Seq2Seq Parameter
n_step = max([max(len(i), len(j)) for i, j in seq_data]) # max_len(=5)
n_hidden = 128
n_class = len(letter2idx) # classfication problem
batch_size = 3
def make_data(seq_data):
enc_input_all, dec_input_all, dec_output_all = [], [], []
for seq in seq_data:
for i in range(2):
seq[i] = seq[i] + '?' * (n_step - len(seq[i])) # 'man??', 'women'
enc_input = [letter2idx[n] for n in (seq[0] + 'E')] # ['m', 'a', 'n', '?', '?', 'E']
dec_input = [letter2idx[n] for n in ('S' + seq[1])] # ['S', 'w', 'o', 'm', 'e', 'n']
dec_output = [letter2idx[n] for n in (seq[1] + 'E')] # ['w', 'o', 'm', 'e', 'n', 'E']
enc_input_all.append(np.eye(n_class)[enc_input])
dec_input_all.append(np.eye(n_class)[dec_input])
dec_output_all.append(dec_output) # not one-hot
# make tensor
return torch.Tensor(enc_input_all), torch.Tensor(dec_input_all), torch.LongTensor(dec_output_all)
enc_input_all, dec_input_all, dec_output_all = make_data(seq_data)
class TranslateDataSet(Data.Dataset):
def __init__(self, enc_input_all, dec_input_all, dec_output_all):
self.enc_input_all = enc_input_all
self.dec_input_all = dec_input_all
self.dec_output_all = dec_output_all
def __len__(self): # return dataset size
return len(self.enc_input_all)
def __getitem__(self, idx):
return self.enc_input_all[idx], self.dec_input_all[idx], self.dec_output_all[idx]
loader = Data.DataLoader(TranslateDataSet(enc_input_all, dec_input_all, dec_output_all), batch_size, True)
# Model
class Seq2Seq(nn.Module):
def __init__(self):
super(Seq2Seq, self).__init__()
self.encoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # encoder
self.decoder = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.5) # decoder
self.fc = nn.Linear(n_hidden, n_class)
def forward(self, enc_input, enc_hidden, dec_input):
enc_input = enc_input.transpose(0, 1) # enc_input: [n_step+1, batch_size, n_class]
dec_input = dec_input.transpose(0, 1) # dec_input: [n_step+1, batch_size, n_class]
# h_t : [num_layers(=1) * num_directions(=1), batch_size, n_hidden]
_, h_t = self.encoder(enc_input, enc_hidden)
# outputs : [n_step+1, batch_size, num_directions(=1) * n_hidden(=128)]
outputs, _ = self.decoder(dec_input, h_t)
model = self.fc(outputs) # model : [n_step+1, batch_size, n_class]
return model
model = Seq2Seq().to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(5000):
for enc_input_batch, dec_input_batch, dec_output_batch in loader:
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
h_0 = torch.zeros(1, batch_size, n_hidden).to(device)
(enc_input_batch, dec_intput_batch, dec_output_batch) = (
enc_input_batch.to(device), dec_input_batch.to(device), dec_output_batch.to(device))
# enc_input_batch : [batch_size, n_step+1, n_class]
# dec_intput_batch : [batch_size, n_step+1, n_class]
# dec_output_batch : [batch_size, n_step+1], not one-hot
pred = model(enc_input_batch, h_0, dec_intput_batch)
# pred : [n_step+1, batch_size, n_class]
pred = pred.transpose(0, 1) # [batch_size, n_step+1(=6), n_class]
loss = 0
for i in range(len(dec_output_batch)):
# pred[i] : [n_step+1, n_class]
# dec_output_batch[i] : [n_step+1]
loss += criterion(pred[i], dec_output_batch[i])
if (epoch + 1) % 1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Test
def translate(word):
enc_input, dec_input, _ = make_data([[word, '?' * n_step]])
enc_input, dec_input = enc_input.to(device), dec_input.to(device)
# make hidden shape [num_layers * num_directions, batch_size, n_hidden]
hidden = torch.zeros(1, 1, n_hidden).to(device)
output = model(enc_input, hidden, dec_input)
# output : [n_step+1, batch_size, n_class]
predict = output.data.max(2, keepdim=True)[1] # select n_class dimension
decoded = [letter[i] for i in predict]
translated = ''.join(decoded[:decoded.index('E')])
return translated.replace('?', '')
print('test')
print('man ->', translate('man'))
print('mans ->', translate('mans'))
print('king ->', translate('king'))
print('black ->', translate('black'))
print('up ->', translate('up'))
print('old ->', translate('old'))
print('high ->', translate('high'))
参考:
序列到序列模型,了解一下 - 知乎 (zhihu.com)