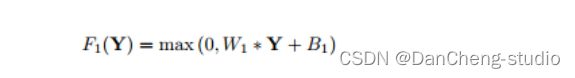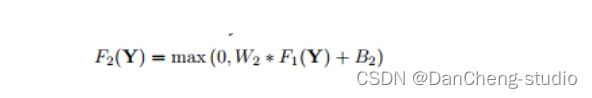大数据毕设选题 - 深度学习图像超分辨率重建(opencv python cnn)
文章目录
- 0 前言
- 1 什么是图像超分辨率重建
- 2 应用场景
- 3 实现方法
- 4 SRResNet算法原理
- 5 SRCNN设计思路
- 6 代码实现
-
- 6.1 代码结构组织
- 6.2 train_srresnet
- 6.3 训练效果
- 7 最后
0 前言
Hi,大家好,这里是丹成学长的毕设系列文章!
对毕设有任何疑问都可以问学长哦!
这两年开始,各个学校对毕设的要求越来越高,难度也越来越大… 毕业设计耗费时间,耗费精力,甚至有些题目即使是专业的老师或者硕士生也需要很长时间,所以一旦发现问题,一定要提前准备,避免到后面措手不及,草草了事。
为了大家能够顺利以及最少的精力通过毕设,学长分享优质毕业设计项目,今天要分享的新项目是
基于深度学习的图像超分辨率重建
学长这里给一个题目综合评分(每项满分5分)
- 难度系数:4分
- 工作量:4分
- 创新点:3分
选题指导, 项目分享:
https://gitee.com/yaa-dc/BJH/blob/master/gg/cc/README.md
1 什么是图像超分辨率重建
图像的超分辨率重建技术指的是将给定的低分辨率图像通过特定的算法恢复成相应的高分辨率图像。具体来说,图像超分辨率重建技术指的是利用数字图像处理、计算机视觉等领域的相关知识,借由特定的算法和处理流程,从给定的低分辨率图像中重建出高分辨率图像的过程。其旨在克服或补偿由于图像采集系统或采集环境本身的限制,导致的成像图像模糊、质量低下、感兴趣区域不显著等问题。
简单来理解超分辨率重建就是将小尺寸图像变为大尺寸图像,使图像更加“清晰”。具体效果如下图所示
2 应用场景
图像超分辨率重建技术在多个领域都有着广泛的应用范围和研究意义。主要包括:
(1) 图像压缩领域
在视频会议等实时性要求较高的场合,可以在传输前预先对图片进行压缩,等待传输完毕,再由接收端解码后通过超分辨率重建技术复原出原始图像序列,极大减少存储所需的空间及传输所需的带宽。
(2) 医学成像领域
对医学图像进行超分辨率重建,可以在不增加高分辨率成像技术成本的基础上,降低对成像环境的要求,通过复原出的清晰医学影像,实现对病变细胞的精准探测,有助于医生对患者病情做出更好的诊断。
(3) 遥感成像领域
高分辨率遥感卫星的研制具有耗时长、价格高、流程复杂等特点,由此研究者将图像超分辨率重建技术引入了该领域,试图解决高分辨率的遥感成像难以获取这一挑战,使得能够在不改变探测系统本身的前提下提高观测图像的分辨率。
(4) 公共安防领域
公共场合的监控设备采集到的视频往往受到天气、距离等因素的影响,存在图像模糊、分辨率低等问题。通过对采集到的视频进行超分辨率重建,可以为办案人员恢复出车牌号码、清晰人脸等重要信息,为案件侦破提供必要线索。
(5) 视频感知领域
通过图像超分辨率重建技术,可以起到增强视频画质、改善视频的质量,提升用户的视觉体验的作用。
3 实现方法
首先介绍图像超分辨率重建技术,图像超分辨率重建技术分为两种,一种是从多张低分辨率图像合成一张高分辨率图像,另外一种是从单张低分辨率图像获取高分辨率图像,在本专栏中,我们使用单幅图像超分辨率重建技术(SISR)。
在这些方法中,可以分为三类,基于插值,基于重建,基于学习。基于插值的方法实现简单,已经广泛应用,但是这些线性的模型限制住了它们恢复高频能力的细节。基于稀疏表示的技术[1]通过使用先验知识增强了线性模型的能力。这类技术假设任意的自然图像可以被字典的元素稀疏表示,这种字典可以形成一个数据库且从数据库中学习到低分辨率图像到高分辨率图像的映射,但是这类方法计算复杂,需要大量计算资源。
基于CNN(卷积神经网络)的模型SRCNN[2]首先将CNN引入SISR中,它仅仅使用三层网络,就取得了先进的结果。随后,各种基于深度学习的模型,进入SISR领域,大致分为以下两个大的方向。一种是追求细节的恢复,以PSNR,SSIM等评价标准的算法,其中以SRCNN模型为代表。另外一种以降低感知损失为目标,不注重细节,看重大局观,以SRGAN[3]为代表的一系列算法。两种不同方向的算法,应用的领域也不相同。在医学图像领域,医生需要图像的细节,以致于做出精确的判断,而不是追求图像整体的清晰,因此,本专栏中将研究追求细节恢复的算法,以及在医学上的应用。
追求细节恢复的算法,也分为两个流派,一是使用插值作为预处理的算法,二是不使用插值,将上采样过程融入网络中的算法。
4 SRResNet算法原理
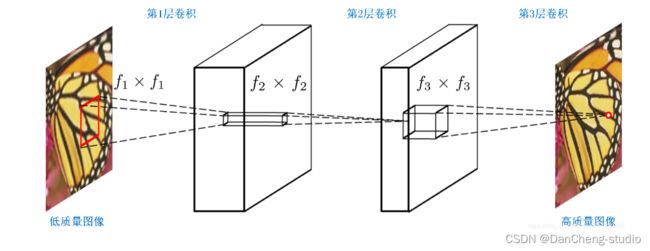
SRCNN的网络结构图如下
三层的作用
在进入网络之前会有将input图像用双三次插值放大至目标尺寸的预处理。
LR 特征提取(Patch extraction and representation),这个阶段主要是对LR进行特征提取,并将其特征表征为一些feature maps;
特征的非线性映射(Non-linear mapping),这个阶段主要是将第一阶段提取的特征映射至HR所需的feature maps;
HR重建(Reconstruction),这个阶段是将第二阶段映射后的特征恢复为HR图像。
网络结构细节
LR特征提取可表征为“卷积层(cf1f1卷积核)+RELU",c是通道数,f1是卷积核的大小。
非线性映射可表征为“全连接层+RELU”,而全连接层又可表征为卷积核为1x1的卷积层,因此,本层最终形式为“卷积层(n111卷积核)+RELU";n1是第一层卷积核的个数。
HR重建可直接表征为“卷积层(n2f3f3)”;n2是第二层卷积核的个数。
5 SRCNN设计思路
这个思路是从稀疏编码得来的,并把上述过程分别表述为:Patch extraction, Non-linear mapping, Reconstruction。
Patch extraction: 提取图像Patch,进行卷积提取特征,类似于稀疏编码中的将图像patch映射到低分辨率字典中。基于样例的算法目的是找到一组可以表达之前预处理后所得到图像块的一组“基”,这些基是沿着不同方向的边缘,稀疏系数就是分配给各个基的权重。作者认为这部分可以转化为用一定数量的滤波器(卷积核)来代替。
Non-linear mapping: 将低分辨率的特征映射为高分辨率特征,类似于字典学习中的找到图像patch对应的高分辨字典。基于样例的算法将第一步得到的表达图像块的高维向量映射到另外一个高维向量中,通过这个高维向量表达高分辨率图像块,用于最后的重建。作者认为这一步骤可以使用1*1的卷积来实现向量维数的变换。
Reconstruction:根据高分辨率特征进行图像重建。类似于字典学习中的根据高分辨率字典进行图像重建。基于样例的算法将最后得到的高分辨率图像块进行聚合(重合的位置取平均)形成最后的高分辨率图像。作者认为这一部分可以看成是一种线性运算,可以构造一个线性函数(不加激活函数)来实现。
从实际操作上来看,整个超分重建分为两步:图像放大和修复。所谓放大就是采用某种方式(SRCNN采用了插值上采样)将图像放大到指定倍数,然后再根据图像修复原理,将放大后的图像映射为目标图像。超分辨率重建不仅能够放大图像尺寸,在某种意义上具备了图像修复的作用,可以在一定程度上削弱图像中的噪声、模糊等。因此,超分辨率重建的很多算法也被学者迁移到图像修复领域中,完成一些诸如jpep压缩去燥、去模糊等任务。
6 代码实现
6.1 代码结构组织
项目根目录下有8个.py文件和2个文件夹,下面对各个文件和文件夹进行简单说明。
- create_data_lists.py:生成数据列表,检查数据集中的图像文件尺寸,并将符合的图像文件名写入JSON文件列表供后续Pytorch调用;
- datasets.py:用于构建数据集加载器,主要沿用Pytorch标准数据加载器格式进行封装;
- models.py:模型结构文件,存储各个模型的结构定义;
- utils.py:工具函数文件,所有项目中涉及到的一些自定义函数均放置在该文件中;
- train_srresnet.py:用于训练SRResNet算法;
- train_srgan.py:用于训练SRGAN算法;
- eval.py:用于模型评估,主要以计算测试集的PSNR和SSIM为主;
- test.py:用于单张样本测试,运用训练好的模型为单张图像进行超分重建;
- data:用于存放训练和测试数据集以及文件列表;
- results:用于存放运行结果,包括训练好的模型以及单张样本测试结果;
整个代码运行顺序如下:
- 运行create_data_lists.py文件用于为数据集生成文件列表;
- 运行train_srresnet.py进行SRResNet算法训练,训练结束后在results文件夹中会生成checkpoint_srresnet.pth模型文件;
- 运行eval.py文件对测试集进行评估,计算每个测试集的平均PSNR、SSIM值;
- 运行test.py文件对results文件夹下名为test.jpg的图像进行超分还原,还原结果存储在results文件夹下面;
- 运行train_srgan.py文件进行SRGAN算法训练,训练结束后在results文件夹中会生成checkpoint_srgan.pth模型文件;
- 修改并运行eval.py文件对测试集进行评估,计算每个测试集的平均PSNR、SSIM值;
- 修改并运行test.py文件对results文件夹下名为test.jpg的图像进行超分还原,还原结果存储在results文件夹下面;
6.2 train_srresnet
代码过多,仅展示关键代码,需要源码的可以call学长
import torch.backends.cudnn as cudnn
import torch
from torch import nn
from torchvision.utils import make_grid
from torch.utils.tensorboard import SummaryWriter
from models import SRResNet
from datasets import SRDataset
from utils import *
# 数据集参数
data_folder = './data/' # 数据存放路径
crop_size = 96 # 高分辨率图像裁剪尺寸
scaling_factor = 4 # 放大比例
# 模型参数
large_kernel_size = 9 # 第一层卷积和最后一层卷积的核大小
small_kernel_size = 3 # 中间层卷积的核大小
n_channels = 64 # 中间层通道数
n_blocks = 16 # 残差模块数量
# 学习参数
checkpoint = None # 预训练模型路径,如果不存在则为None
batch_size = 400 # 批大小
start_epoch = 1 # 轮数起始位置
epochs = 130 # 迭代轮数
workers = 4 # 工作线程数
lr = 1e-4 # 学习率
# 设备参数
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
ngpu = 2 # 用来运行的gpu数量
cudnn.benchmark = True # 对卷积进行加速
writer = SummaryWriter() # 实时监控 使用命令 tensorboard --logdir runs 进行查看
def main():
"""
训练.
"""
global checkpoint,start_epoch,writer
# 初始化
model = SRResNet(large_kernel_size=large_kernel_size,
small_kernel_size=small_kernel_size,
n_channels=n_channels,
n_blocks=n_blocks,
scaling_factor=scaling_factor)
# 初始化优化器
optimizer = torch.optim.Adam(params=filter(lambda p: p.requires_grad, model.parameters()),lr=lr)
# 迁移至默认设备进行训练
model = model.to(device)
criterion = nn.MSELoss().to(device)
# 加载预训练模型
if checkpoint is not None:
checkpoint = torch.load(checkpoint)
start_epoch = checkpoint['epoch'] + 1
model.load_state_dict(checkpoint['model'])
optimizer.load_state_dict(checkpoint['optimizer'])
if torch.cuda.is_available() and ngpu > 1:
model = nn.DataParallel(model, device_ids=list(range(ngpu)))
# 定制化的dataloaders
train_dataset = SRDataset(data_folder,split='train',
crop_size=crop_size,
scaling_factor=scaling_factor,
lr_img_type='imagenet-norm',
hr_img_type='[-1, 1]')
train_loader = torch.utils.data.DataLoader(train_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=workers,
pin_memory=True)
# 开始逐轮训练
for epoch in range(start_epoch, epochs+1):
model.train() # 训练模式:允许使用批样本归一化
loss_epoch = AverageMeter() # 统计损失函数
n_iter = len(train_loader)
# 按批处理
for i, (lr_imgs, hr_imgs) in enumerate(train_loader):
# 数据移至默认设备进行训练
lr_imgs = lr_imgs.to(device) # (batch_size (N), 3, 24, 24), imagenet-normed 格式
hr_imgs = hr_imgs.to(device) # (batch_size (N), 3, 96, 96), [-1, 1]格式
# 前向传播
sr_imgs = model(lr_imgs)
# 计算损失
loss = criterion(sr_imgs, hr_imgs)
# 后向传播
optimizer.zero_grad()
loss.backward()
# 更新模型
optimizer.step()
# 记录损失值
loss_epoch.update(loss.item(), lr_imgs.size(0))
# 监控图像变化
if i==(n_iter-2):
writer.add_image('SRResNet/epoch_'+str(epoch)+'_1', make_grid(lr_imgs[:4,:3,:,:].cpu(), nrow=4, normalize=True),epoch)
writer.add_image('SRResNet/epoch_'+str(epoch)+'_2', make_grid(sr_imgs[:4,:3,:,:].cpu(), nrow=4, normalize=True),epoch)
writer.add_image('SRResNet/epoch_'+str(epoch)+'_3', make_grid(hr_imgs[:4,:3,:,:].cpu(), nrow=4, normalize=True),epoch)
# 打印结果
print("第 "+str(i)+ " 个batch训练结束")
# 手动释放内存
del lr_imgs, hr_imgs, sr_imgs
# 监控损失值变化
writer.add_scalar('SRResNet/MSE_Loss', loss_epoch.val, epoch)
# 保存预训练模型
torch.save({
'epoch': epoch,
'model': model.module.state_dict(),
'optimizer': optimizer.state_dict()
}, 'results/checkpoint_srresnet.pth')
# 训练结束关闭监控
writer.close()
if __name__ == '__main__':
main()
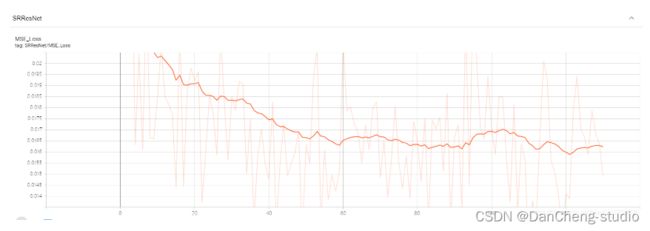
6.3 训练效果
训练共用时15小时19分6秒(没有用显卡),训练完成后保存的模型共17.8M。下图展示了训练过程中的损失函数变化。可以看到,随着训练的进行,损失函数逐渐开始收敛,在结束的时候基本处在收敛平稳点。