光谱异常样本检测分析
以近红外光谱为例,大部分光谱数据在不考虑分类问题时,在构建模型前需要对采集数据进行样本分析,以降低因生产过程异常、人为误操作和其他原因对软测量模型的影响,即异常样本检测分析。
按照定义,异常样本检测任务指的是检测偏离期望行为的事件或者模式,可以是简单地检测数值型数据中是否存在远超于正常范围的离群值,也可以是借助相对复杂的机器学习算法识别数据中隐藏的异常模式。
1定义及类别
异常样本分为:
(1) 离群值(Outlier):偏离正常范围的数据,可能是由传感器故障、人为录入错误或者异常事件导致,在构建机器学习或者统计模型前,可能会导致模型出现偏差。
(2) 奇异值(Novelty):数据集未受到异常值污染,但是存在某些区别于原始数据分布的观测数据。
从统计分析角度看,离群值指的是破坏正常数据分布的数据,而奇异数据则是丰富正常数据分布的数据;从模型性能角度看,离群值是降低模型性能的样本,而奇异值则是可能提高模型性能的样本。
2分析思路
异常样本检测分析思路:
(1) 了解你的数据;
首先,你需要充分了解你的数据及数据所属对象的专业背景,不同类型数据对于异常样本的理解是存在差异的,通常包括以下思路:
(a) 原始数据中的异常是否显而易见的?
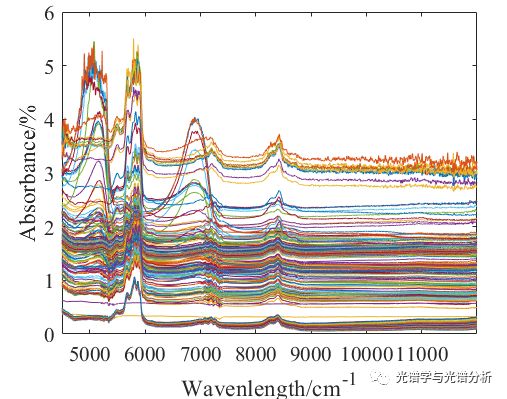
对于复杂生产过程或不稳定测量环境下获得的样品光谱,其异常样本是比较明显的,如下图所示,存在明显的异常光谱,其主要原因是在线光纤探头堵塞造成的谱线异常。值得注意的是,很多异常样本是无法通过人眼观测的,甚至需要很多工程经验才能做到初步辨识,这也是很多模型泛化性无法进一步提升的因素之一,此类情况下,只能借助其他工具辨识异常样本。
(b) 从原始数据中是否可以提取出能够有效区分异常的特征?
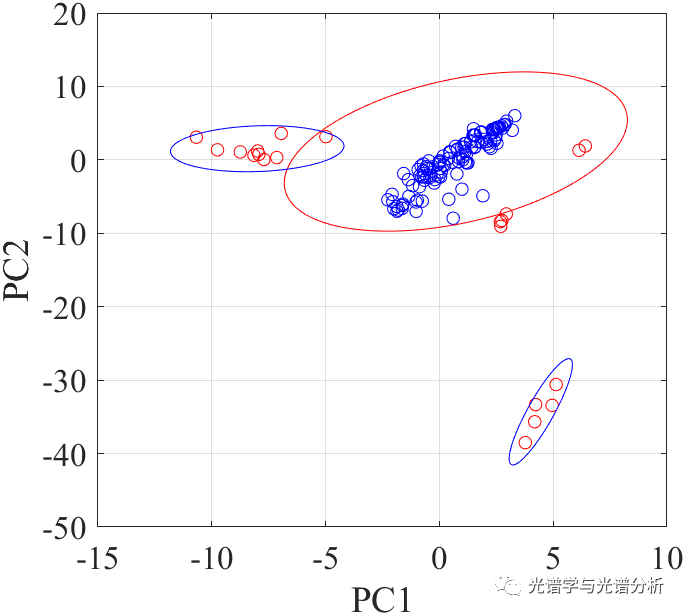
针对(a)之外的异常问题,我们能否聚焦于正常和异常样本的可区分特征,这里的特征可以是原始的或者变换后的,例如降维后的、高维扩增后的或者从时域变换为频域的。例如针对图1很难通过人工筛选全部异常样本的情况下,通过PCA降维后可以较为明显的区分正常和异常样本。
(c) 从统计分析的角度去区分正常和异常样本
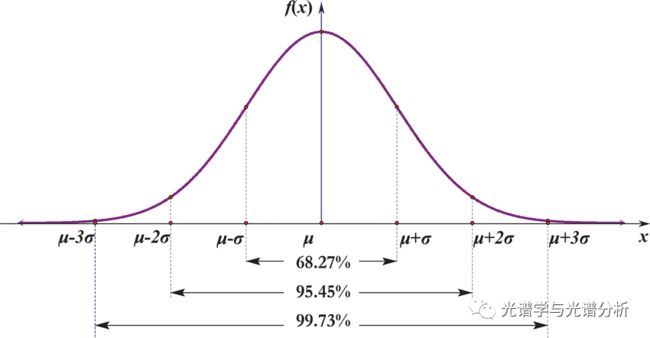
此方法主要基于实测数据的统计分布特性,对于一个稳定或者自然过程,其采集数据通常服从某种分布,多采用正态分布去表征不确定具体分布的过程数据。基于实测数据的统计分析,我们有理由相信正常样本是在变动区间的界限内分布,并且在特定范围存在的概率小于某一近似值。以正态分布为例,数据分布在正负3个标准差范围内的概率为99.73%,因此,可将超出此范围的数据认定为异常样本。
(d) 对于无法确定是否存在异常样本的数据,我们应该如何处理?
对于全天候设备,或者连续生产设备,故障导致的停机意味着产能降低甚至造成重大安全问题。此类问题的显著特征是异常数据稀缺,且能够采集到的数据全部或者大部分为正常数据,此类情况下异常样本检测认为被处理为无监督学习问题,可通过数据的隐藏特性筛选异常样本。一个典型的例子是利用过程的时序性,建立LSTM模型,监测输出值的变化趋势实现异常样本的预警分析。
(2) 选择合适的方法;
根据所测变量维度的不同,通常分为一维和高维异常样本分析,可以理解为多个样本的单个指标就是一维,多个样本的多维光谱就是高维,两者的异常样本选择方法是存在明显差异的。
3分析方法
01一维数据分析方法
(a) 是否超出历史数据的最大/最小值;
此方法是最大容错限度,通常情况下不会以历史数据的极值作为批判标准,更多的是结合统计过程控制(statistical process control, SPC)建立合适的批判上下限进行样本分析。
(b) 3-sigma原则;
如果数据符合正态分布,可将3sigma作为误差极限,将落在[u-3sigma, u+3sigma]外的样本作为离群值;以某数据为例,其分布统计图如下所示,可根据数据分布选择性地确定离群阈值线并确定对应样本。
(c) 利用箱线图/四分位图检验
箱线图或者箱型图可以反映数据的整体分布情况,因此可以用于判断数据是否存在异常值,如下图所示,可以较为明显地判断是否有异常及异常值的判断上下界。此外,结合其他指标可以确定对应异常值的索引,并最终确定异常样本。
02高维数据分析方法
对于多变量数据集,特征之间可能存在复杂和高度非线性的相关性,上述方法不再适用于异常样本分析,通常采用以下检测方法:
(a) 高维数据可视化分析
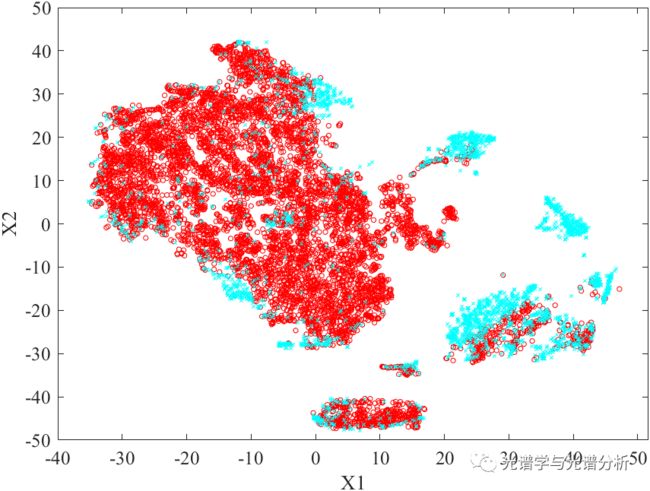
可视化分析包括统计分布可视化、聚类分布可视化和降维可视化等,此外包括升维可视化,主要目的是将低维不可分问题转换为高维线性可分问题。以某数据为例,其利用tSNE降维后的数据可区分性得以提升。
(b) 有监督异常检测
可以根据采集有标签样本数据建立分类模型实现异常样本检测,例如朴素贝叶斯分类模型,CNN模型等,此处不再详细介绍。
(c) 无监督异常检测
对于没有标签信息的多变量样本数据,可以通过数据自身的特性出发进行无监督异常分析,例如基于距离类的、基于统计类的、基于因子分析类的等等。此处介绍几种基于距离类的方法。
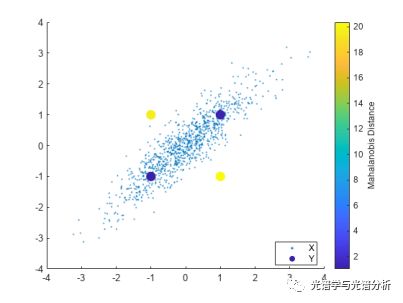
1) 马氏距离(Mahalanobis Distance),该方法是一种衡量样本和数据集分布间相似度的尺度无关的度量指标。具体为如果数据符合多变量正态分布,那么可以使用样本到数据集分布中心的马氏距离检测异常。此处需要简单解释一下为什么不建议采用欧式距离,如下图所示,图中蓝色点和黄色点离样本均值的欧式距离相近,但是由于样本整体分布沿 f(x)=x 的方向分布(变量之间具有相关性),蓝色点更有可能是数据集中的点,对应的马氏距离更小,而黄色点更有可能是离群值,对应马氏距离也更大。因此,设定一个合理的阈值,可以划分异常样本和正常样本。
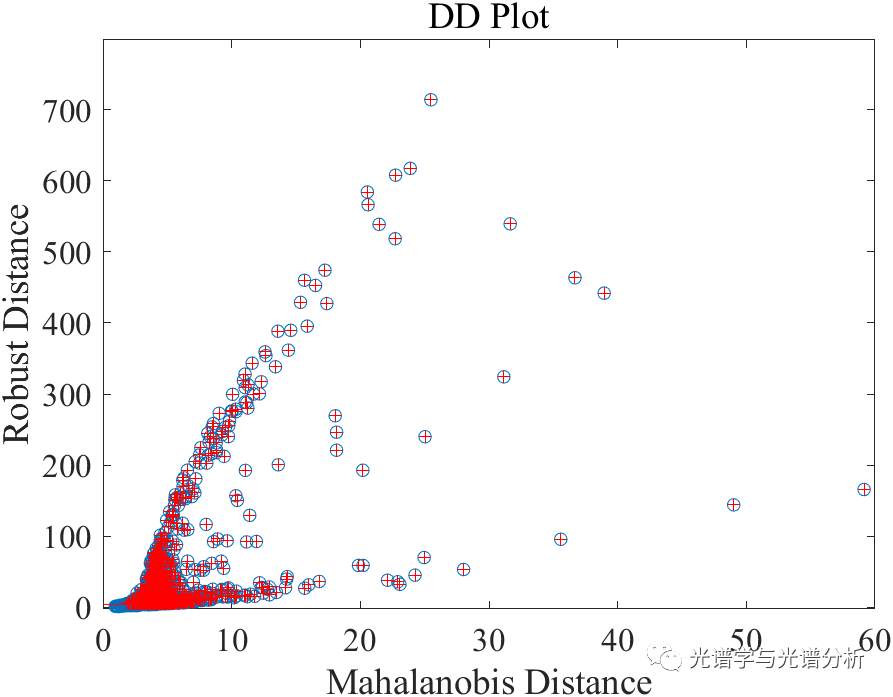
对于上述的某数据集,基于马氏距离的方法可较好的实现异常样本筛选。
值得一提的是,马氏距离筛选异常样本适用于数据符合或接近正态分布的情况,但在通常情况下,实际数据的分布规律难以预估。
2) 局部离群因子法:通过计算样本及其周围k个近邻点的局部可达密度并量化每个样本的离群程度确定离群样本,该方法不受数据分布的影响,同时考虑了数据集的局部和全局属性,比较适用于中等高维的数据集,针对示例数据集的预测准确度比较理想。但对近邻参数较为敏感,由于需要计算数据集中任意两个数据点的距离,算法的时间复杂度较高,在大规模数据集上效率偏低,适合小规模到中等规模的数值型数据。
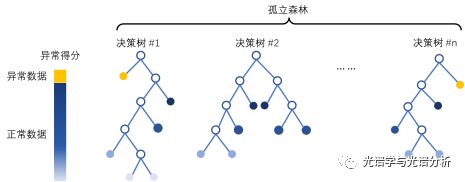
3) 孤立森林:利用决策树模型对样本进行划分,并根据路径长度确定异常样本。
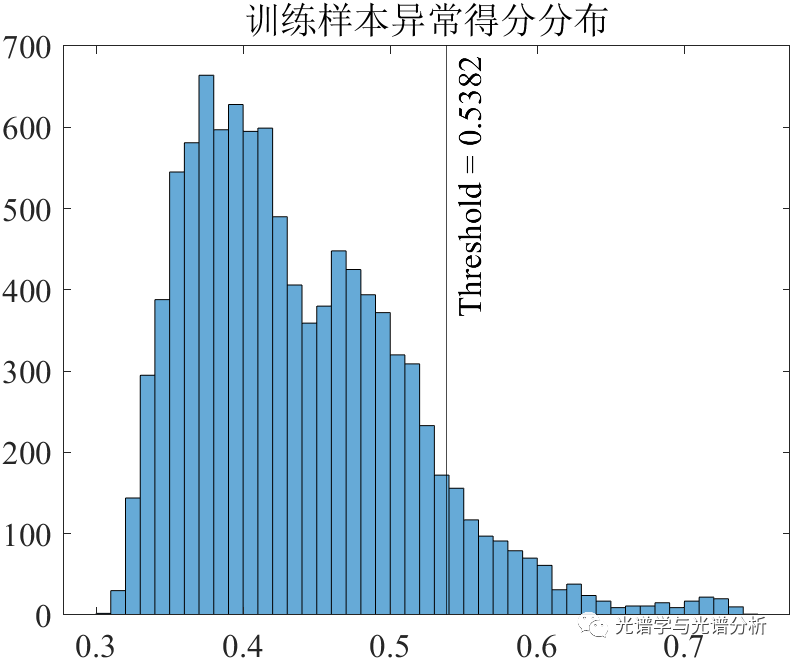
对于上述某数据,我们可得到如下样本得分统计分布并确定阈值线,根据阈值可确定最终的异常样本。
4总结回顾
1. 在处理数据前,首先要结合专业背景充分了解你的数据;
2. 熟悉不同异常样本检测方法的适用范围或特定条件,根据实际情况选择合适的方法。
3. 转换思考角度,从不同方面去看异常样本的特性;
4. 尊重实际过程问题,数据来源于实际,脱离实际问题,很多方法无法发挥作用。
如果您有感兴趣的话题、其他观点或者问题,欢迎留言或者发送邮件。