高光谱图像异常检测论文总结(一)
论文
Discriminative Reconstruction Constrained Generative Adversarial Network for Hyperspectral Anomaly Detection
过程
流程图
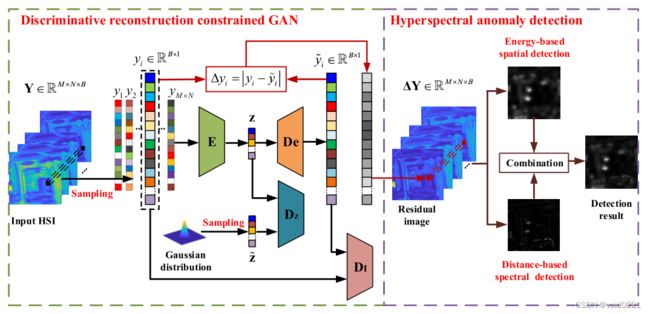
总体流程图
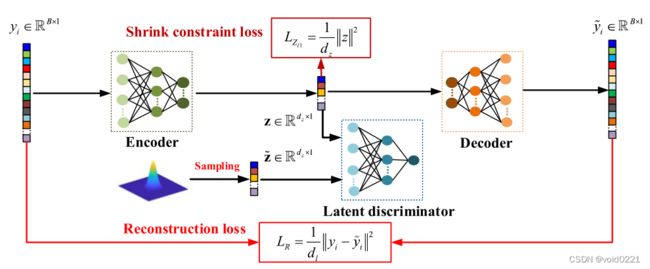
自动编码器流程图
损失函数
- 原始图像和生成图像的均方误差损失: L R = 1 d l ∥ y i − D e ( E ( y i ) ) ∥ 2 L_R=\frac{1}{d_l}\left\| y_i-De\left( E\left( y_i \right) \right) \right\| ^2 LR=dl1∥yi−De(E(yi))∥2, y i ∈ R B × 1 y_i\in \mathbb{R} ^{B\times 1} yi∈RB×1, d l d_l dl是输入样本空间的维数
- 潜在向量通过解码器后再次通过编码器映射回潜在特征层的均方误差损失: L z i z = 1 d z ∥ z − E ( D e ( z ) ) ∥ 2 L_{ziz}=\frac{1}{d_z}\left\| z-E\left( De\left( z \right) \right) \right\| ^2 Lziz=dz1∥z−E(De(z))∥2
- 收缩约束的正则损失项。该约束能够惩罚与潜在特征空间中大多数样本分布(即背景分布)存在较大向量偏差的样本点。 L Z l 1 = 1 d z ∥ z ∥ 2 L_{Z_{l1}}=\frac{1}{d_z}\left\| z \right\| ^2 LZl1=dz1∥z∥2
然后将上述三个损失函数加权可得: L = α 0 L R + α 1 L z i z + α 2 L Z l 1 L=\alpha _0L_R+\alpha _1L_{ziz}+\alpha _2L_{Z_{l1}} L=α0LR+α1Lziz+α2LZl1,其中 α 0 \alpha _0 α0 = 1, α 1 \alpha _1 α1 = 1, α 2 \alpha _2 α2 = 0.1。
基于能量的空间异常检测器
通过像素级残差运算得到残差图像 Δ Y = ∣ Y − Y ~ ∣ ∈ R M × N × B \varDelta Y=\left| Y-\tilde{Y} \right|\in \mathbb{R} ^{M\times N\times B} ΔY=∣∣∣Y−Y~∣∣∣∈RM×N×B
最小背景信息是指二维图像中与频带相对应的大多数背景像素的能量值趋于零,因此满足要求的频带应该是总能量值最小的频带。确定总能量值的标准为 ∑ j = 0 N − 1 ∑ i = 0 M − 1 e ( i , j ) \sum_{j=0}^{N-1}{\sum_{i=0}^{M-1}{e\left( i,j \right)}} ∑j=0N−1∑i=0M−1e(i,j),其中i和j表示空间坐标, e ( i , j ) e\left( i,j \right) e(i,j)表示 ( i , j ) \left( i,j \right) (i,j)处像素的灰度值。选择具有最小能量值的三个带 { B s , s = 1 , 2 , 3 } \left\{B_s,s=1,2,3\right\} {Bs,s=1,2,3}。
应用属性打开操作 O ( B s ) O\left( Bs \right) O(Bs)来移除具有特定区域属性的亮连接组件,并且还应用属性关闭操作 C ( B s ) C\left(Bs \right) C(Bs)来清除具有相同特定区域的暗连接组件。为了保留所有小区域异常,无论是亮还是暗,计算滤波图像和原始图像之间的剩余 D f ( B s ) D_f\left(Bs \right) Df(Bs)以去除背景。 D f ( B s ) = ∣ B s − O ( B s ) ∣ + ∣ C ( B s ) − B s ∣ , s = 1 , 2 , 3 D_f\left( B_s \right) =\left| B_s-O\left( B_s \right) \right|+\left| C\left( B_s \right) -B_s \right|, s=1,2,3 Df(Bs)=∣Bs−O(Bs)∣+∣C(Bs)−Bs∣,s=1,2,3。
然后进行融合,平滑噪声像素,丢弃冗余信息,提取有用的空间信息。 F = 1 3 ∑ s = 1 3 D f ( B s ) F=\frac{1}{3}\sum_{s=1}^3{D_f\left( B_s \right)} F=31∑s=13Df(Bs)。
考虑到融合图像的局部平滑先验,采用引导滤波器对融合图像进行细化。 D s p a t i a l = { D i ∣ D i = a ˉ i F i + b ˉ i , i = 1 , . . . , M × N } D_{spatial}=\left\{ D_i \mid D_i=\bar{a}_iF_i+\bar{b}_i, i=1, ..., M\times N \right\} Dspatial={Di∣Di=aˉiFi+bˉi,i=1,...,M×N}。其中 ( a ˉ i , b ˉ i ) \left( \bar{a}_i, \bar{b}_i \right) (aˉi,bˉi)是不同局部窗口重叠i的线性系数的平均值。局部窗口中输入和滤波输出之间的平方差最小化,以获得线性系数。对于所有测试数据集,引导滤波器的两个系数(滤波器大小和模糊度)分别设置为3和0.5。
基于距离的光谱异常检测器
在光谱域中,残差图像 Δ Y \varDelta Y ΔY表示为 Δ Y = [ Δ y 1 , Δ y 2 , . . . , Δ y M × N ] \varDelta Y=\left[ \varDelta y_1, \varDelta y_2, ..., \varDelta y_{M\times N} \right] ΔY=[Δy1,Δy2,...,ΔyM×N],其具有 B B B维的 M × N M\times N M×N个向量。采用最常见的基于距离的RX探测器: D s p e c t r a l = ( Δ y p − μ ) T Γ − 1 ( Δ y p − μ ) , p = 1 , . . . , M × N D_{spectral}=\left( \varDelta y_p-\mu \right) ^T\varGamma ^{-1}\left( \varDelta y_p-\mu \right) , p=1, ..., M\times N Dspectral=(Δyp−μ)TΓ−1(Δyp−μ),p=1,...,M×N,其中 Δ y p ∈ R B × 1 \varDelta y_p\in \mathbb{R} ^{B\times 1} Δyp∈RB×1是 Δ Y \varDelta Y ΔY的第 p p p个向量, μ ∈ R B × 1 \mu \in \mathbb{R} ^{B\times 1} μ∈RB×1, Γ ∈ R B × B \varGamma \in \mathbb{R} ^{B\times B} Γ∈RB×B,分别是 Δ Y \varDelta Y ΔY的平均值和协方差矩阵
空间-光谱联合异常检测器
最后,通过线性组合将两个检测图进行空间 - 光谱联合。 D s s = λ 1 D s p a t i a l + ( 1 − λ 1 ) D s p e c t r a l D_{ss}=\lambda _1D_{spatial}+\left( 1-\lambda _1 \right) D_{spectral} Dss=λ1Dspatial+(1−λ1)Dspectral。其中 λ 1 \lambda _1 λ1是控制空间特征和光谱特征对最终检测结果 D s s D_{ss} Dss贡献的权衡参数, λ 1 = 0.5 \lambda _1=0.5 λ1=0.5。
网络结构与超参数
考虑到高光谱数据的性质,采用了一个四层全连通网络,分别为 E { B , 1000 , 1000 , d z } E \left\{ B, 1000, 1000, d_z \right\} E{B,1000,1000,dz}, D e { d z , 1000 , 1000 , B } De \left\{ d_z,1000,1000, B \right\} De{dz,1000,1000,B}, D I { B , 1000 , 1000 , 1 } D_I \left\{ B,1000,1000,1 \right\} DI{B,1000,1000,1}, D z { d z , 1000 , 1000 , 1 } D_z \left\{ dz,1000,1000,1 \right\} Dz{dz,1000,1000,1}。其中, d z d_z dz是指潜在层的大小, d z = B + 1 d_z=\sqrt{B}+1 dz=B+1, B B B是输入HSI的频带数。
编码器E的所有全连接层之后进行批量归一化和LeakyReLU(斜率为0.2)操作。对于 D e D_e De、 D Z D_Z DZ和 D I D_I DI,全连接层仅使用LeakyReLU(斜率为0.2)作为激活函数。
为了防止AE过拟合,在AE中的潜在层使用了Dropout(默认参数为1.0)。对 E E E和 D e D_e De使用权重因子为 1 0 − 5 10^{−5} 10−5的 L 2 L_2 L2正则化,上述项允许网络中的偏差为0,以消除偏差项对像素组成的影响。
整个框架执行300个epoch,批量大小为M×N。这里选择的epoch数并不能获得最佳的检测结果,但对于所有数据集都是稳定的,并且时间开销很低。学习率固定为0.0001。编码器训练使用自适应学习速率方法RMSprop,其他训练使用随机优化器Adam。