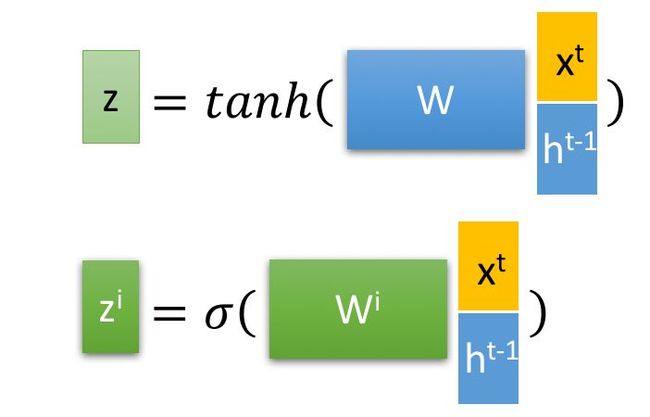GRU是什么？RNN、LSTM分别是什么？

前言

最近在学习图神经网络（GNN）的过程中，遇到很多不懂的地方，深度学习的基础没有掌握好。最早的GNN网络（详情见GNN）可以被用于处理有环图、有向图或无向图。然而，GNN网络本身必须使整个网络达到不动点之后才可以进行计算。针对这一问题，通过将GRU引入到网络结构中，进一步提出了GGNN网络（详情见GGNN）。那么，现在就介绍一下GRU是什么东西。

GRU中的G不是Graph，而是Gate，全称是Gate Recurrent Unit（门循环单元），它是循环神经网络（Recurrent Neural Network, RNN）的一种。和LSTM（Long-Short Term Memory）一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。在R-NET: MACHINE READING COMPREHENSION WITH SELF-MATCHING NETWORKS（2017）文章中提出

译：我们在我们的实验中选择GRU是因为它的实验效果与LSTM相似，但是更易于计算。 

相比LSTM，使用GRU能够达到相当的效果，并且相比之下更容易进行训练，能够很大程度上提高训练效率，因此很多时候会更倾向于使用GRU。在介绍GRU之前，先介绍一下RNN和LSTM。

RNN

循环神经网络（Recurrent Neural Network，RNN）是一种用于处理序列数据的神经网络。相比一般的神经网络来说，它能够处理序列变化的数据。比如某个单词的意思会受上文提到的内容的影响，RNN就能够很好地解决这类问题。

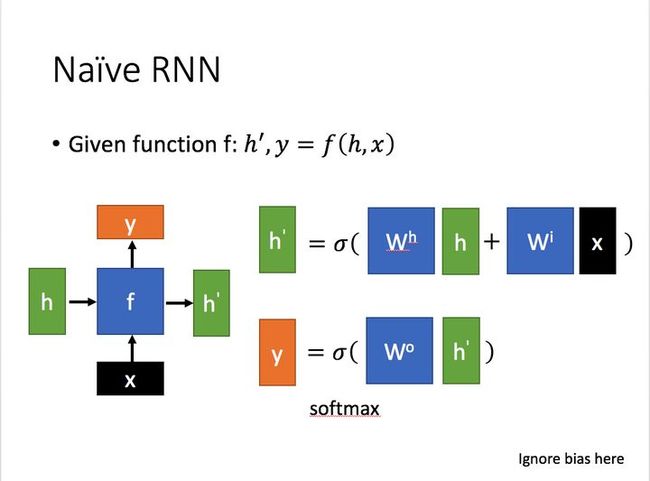
其主要形式如下图所示（台大李宏毅教授的PPT）：

 

这里：

为当前时刻的输入特征，表示上一时刻存储的状态信息。 为当前节点状态下的输出，而  为传递到下一时刻存储的状态信息。通过上图的公式可以看到，状态信息h' 与 当前时刻的输入特征 x 和上一时刻的状态信息 h 的值都相关。而 y 则常常使用 h' 投入到一个线性层（主要是进行维度映射），然后使用softmax进行分类得到需要的数据。对这里的 y 如何通过 h' 计算得到往往看具体模型的使用方式。

第一个激活函数通常用tanh，第二个激活函数用softmax。

前向传播时：记忆体内存储的状态信息，在每个时刻都被刷新，三个参数矩阵自始至终都是固定不变的。
反向传播时：三个参数矩阵被梯度下降法更新。

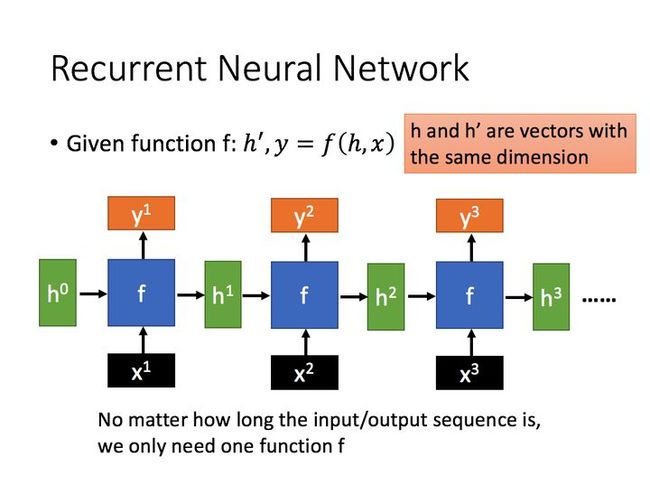
通过序列形式的输入，我们能够得到如下形式的RNN：

上图中一共有三个循环核（循环计算层） 

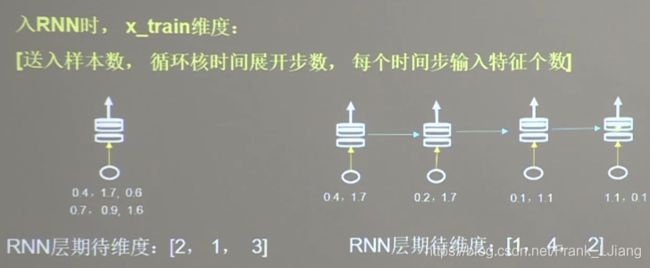
在TensorFlow中，对于RNN输入必须是三个维度，分别是样本的总数，循环核时间展开步数（循环核个数），每个时间步输入的特征个数。如上图所示。

下面给出一个例子：

input_word = "abcde"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4}  # 单词映射到数值id的词典
id_to_onehot = {0: [1., 0., 0., 0., 0.], 1: [0., 1., 0., 0., 0.], 2: [0., 0., 1., 0., 0.], 3: [0., 0., 0., 1., 0.],
                4: [0., 0., 0., 0., 1.]}  # id编码为one-hot

x_train = [id_to_onehot[w_to_id['a']], id_to_onehot[w_to_id['b']], id_to_onehot[w_to_id['c']],
           id_to_onehot[w_to_id['d']], id_to_onehot[w_to_id['e']]]
y_train = [w_to_id['b'], w_to_id['c'], w_to_id['d'], w_to_id['e'], w_to_id['a']]

# 使x_train符合SimpleRNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]。
# 此处整个数据集送入，送入样本数为len(x_train)；输入1个字母出结果，循环核时间展开步数为1; 表示为独热码有5个输入特征，每个时间步输入特征个数为5
x_train = np.reshape(x_train, (len(x_train), 1, 5))
y_train = np.array(y_train)

# 模型 循环核时间展开步数为1
model = tf.keras.Sequential([
    SimpleRNN(3),
    Dense(5, activation='softmax')
])

 

LSTM

长短期记忆（Long short-term memory, LSTM）是一种特殊的RNN，主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说，就是相比普通的RNN，LSTM能够在更长的序列中有更好的表现。

传统的循环神经网络RNN可以通过记忆体实现短期记忆进行连续数据的预测，但是当连续数据的序列变长时，会使展开时间步过长，在反向传播更新参数时，梯度要按照时间步连续相乘，很容易导致梯度消失，所以LSTM就出现了。

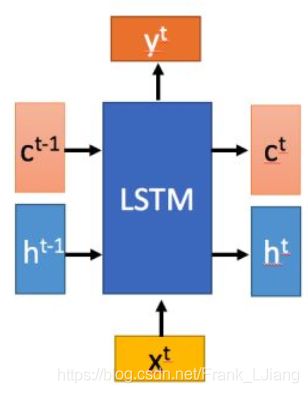
LSTM结构（图右）和普通RNN的主要输入输出区别如下所示：

相比RNN只有一个传递状态 ，LSTM有两个传递状态，一个 （cell state，细胞态，长期记忆），和一个 （hidden state，隐态，记忆体，短期记忆）。（Tips：RNN中的 对于LSTM中的 ） 。其中对于传递下去的  改变得很慢，通常输出的  是上一个状态传过来的  加上一些数值，而  则在不同节点下往往会有很大的区别。

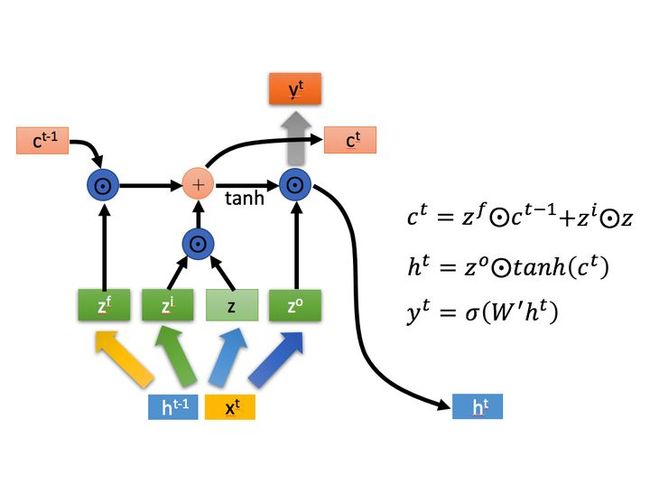
下面具体对LSTM的内部结构来进行剖析：

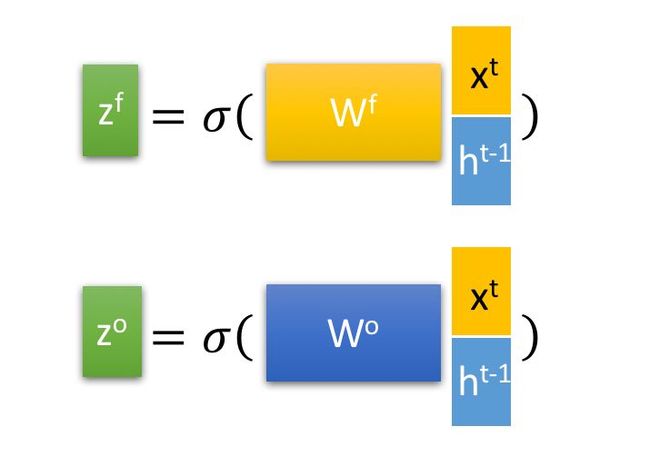
首先使用LSTM的当前输入  和上一个状态传递下来的  拼接训练得到四个状态。

 其中，  是由拼接向量乘以权重矩阵之后，再通过一个  激活函数转换成0到1之间的数值，来作为一种门控状态，分别表示：

 表示输入门， 表示遗忘门， 表示输出门。

而  则是将结果通过一个  激活函数将转换成-1到1之间的值（这里使用  是因为这里是将其做为输入数据，而不是门控信号）， 表示候选态，由上一时刻的短期记忆  和 当前时刻的输入特征  决定。

 （cell state，细胞态，长期记忆）， （hidden state，记忆体，短期记忆） 

 

是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。  则代表进行矩阵加法。 

LSTM内部主要有三个阶段：

1. 遗忘门。这个阶段主要是对上一个节点传进来的输入进行选择性遗忘。简单来说就是会 “忘记不重要的，记住重要的”。

具体来说是通过计算得到的  （f表示forget）来作为忘记门控，来控制上一个状态的  哪些需要留哪些需要忘。

2. 输入门。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入  进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的  表示。而选择的门控信号则是由  （i代表input）来进行控制。

将上面两步得到的结果相加，即可得到传输给下一个状态的   。也就是上上图中的第一个公式。

3. 输出门。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过  来进行控制的。并且还对上一阶段得到的  进行了放缩（通过一个tanh激活函数进行变化）。

与普通RNN类似，输出  往往最终也是通过  变化得到。

以上，就是LSTM的内部结构。通过门控状态来控制传输状态，记住需要长时间记忆的，忘记不重要的信息；而不像普通的RNN那样只能够“呆萌”地仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说，尤其好用。但也因为引入了很多内容，导致参数变多，也使得训练难度加大了很多。因此很多时候我们往往会使用效果和LSTM相当但参数更少的GRU来构建大训练量的模型。

思考：加入这么多门控信息，真的会起作用吗？？？这些门控机制都是通过反向传播学习的，真的会学到吗？？？

例子：

# 测试集变array并reshape为符合RNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))

model = tf.keras.Sequential([
    LSTM(80, return_sequences=True),  # 每个时间步都输出h_t
    Dropout(0.2),
    LSTM(100),  # 只在最后时间步输出h_t
    Dropout(0.2),
    Dense(1)
])

GRU

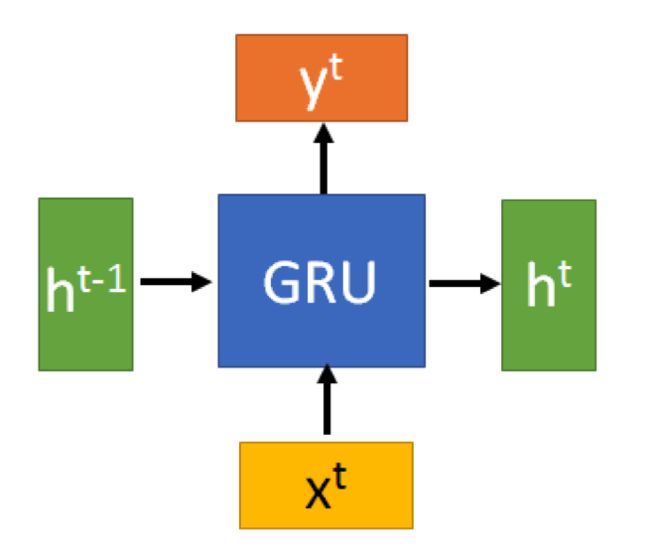
GRU的输入输出结构与普通的RNN是一样的，它的提出是为了解决LSTM计算过于复杂的问题。有一个当前的输入  ，和上一个节点传递下来的隐状态（hidden state）  ，这个隐状态包含了之前节点的相关信息。结合  和 ，GRU会得到当前隐藏节点的输出  和传递给下一个节点的隐状态  。

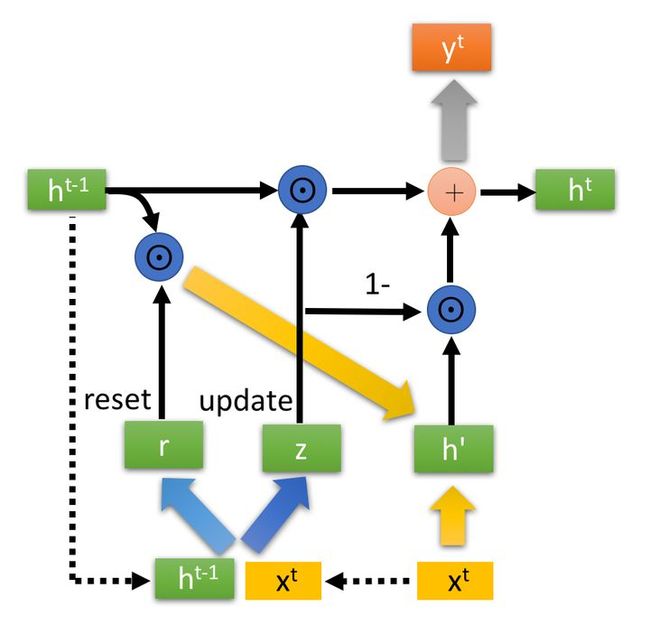
那么，GRU到底有什么特别之处呢？下面来对它的内部结构进行分析！

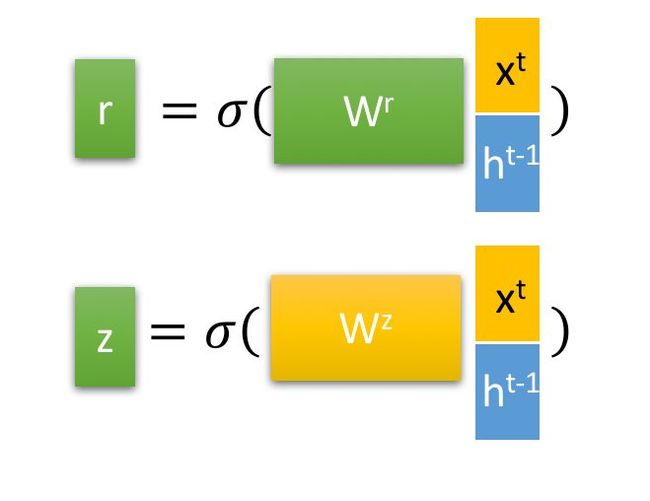
首先，我们先通过上一个传输下来的状态  和当前节点的输入  来获取两个门控状态。如下图所示，其中  控制重置的门控（reset gate），  为控制更新的门控（update gate）。 

Tips：  为sigmoid函数，通过这个函数可以将数据变换为0-1范围内的数值，从而来充当门控信号。

与LSTM分明的层次结构不同，得到门控信号之后，首先使用重置门控来得到“重置”之后的数据

再将  与输入  进行拼接，再通过一个tanh激活函数来将数据放缩到-1~1的范围内。即得到如下图所示的  。

这里的  主要是包含了当前输入的  数据。有针对性地对  添加到当前的隐藏状态。

 是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。  则代表进行矩阵加法操作。 

最后介绍GRU最关键的一个步骤，我们可以称之为”更新记忆“阶段。在这个阶段，我们同时进行了遗忘和记忆两个步骤。我们使用了先前得到的更新门控  （update gate）。相当于遗忘门，1-z 相当于输入门

更新表达式： 

首先再次强调一下，门控信号（这里的  ）的范围为0~1。门控信号越接近1，代表”记忆“下来的数据越多；而越接近0则代表”遗忘“的越多。

GRU很聪明的一点就在于，使用了同一个门控  ，即同时可以进行遗忘和记忆（LSTM则要使用多个门控）。

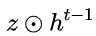•  ：表示对原本隐藏状态的选择性“遗忘”。这里的  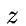可以想象成遗忘门（forget gate），忘记  维度中一些不重要的信息。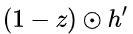
•  ： 表示对包含当前节点信息的  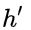进行选择性”记忆“。与上面类似，这里的  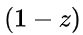同理会记住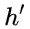中重要的，忘记  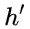维度中的一些不重要的信息。或者，这里我们更应当看做是对  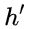维度中的某些信息进行选择。
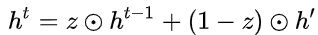•  ：结合上述，这一步的操作就是忘记传递下来的  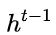中的某些维度信息，并加入当前节点输入的某些维度信息。

可以看到，这里的遗忘   和选择   是联动的。也就是说，对于传递进来的维度信息，我们会进行选择性遗忘，则遗忘了多少权重 （  ），我们就会使用包含当前输入的   中所对应的权重进行弥补   。以保持一种“ 恒定”状态。

# 测试集变array并reshape为符合RNN输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))

model = tf.keras.Sequential([
    GRU(80, return_sequences=True),
    Dropout(0.2),
    GRU(100),
    Dropout(0.2),
    Dense(1)
])

LSTM与GRU的关系

GRU是在2014年提出来的，而LSTM是1997年。他们的提出都是为了解决相似的问题，那么GRU难免会参考LSTM的内部结构。那么他们之间的关系大概是怎么样的呢？这里简单介绍一下。大家看到  (reset gate)实际上与他的名字有点不符。我们仅仅使用它来获得了  。那么这里的  实际上可以看成对应于LSTM中的hidden state；上一个节点传下来的  则对应于LSTM中的cell state。z 对应的则是LSTM中的  forget gate，那么  我们似乎就可以看成是选择门  了。

总结

GRU输入输出的结构与普通的RNN相似，其中的内部思想与LSTM相似。与LSTM相比，GRU内部少了一个”门控“，参数比LSTM少，但是却也能够达到与LSTM相当的功能。考虑到硬件的计算能力和时间成本，因而很多时候我们也就会选择更加“实用”的GRU啦。

RNN

【翻译】理解 LSTM 网络