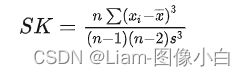数学基础知识：数据统计

前言

图像处理过程中不可避免涉及到很多数学知识，边学习边记录

---

数据统计

一、集中趋势

算术平均数：u=(x1+x2+...Xn)/n

加权平均数：u=(x1*w1+x2*w2+...Xn*wn)/(w1+w2+...+wn)

几何平均数：对各变量值的连乘积开项数次方根，通常用于连乘关系的比率

u=（x1*x2*...*xn）的开n次方根

注：

调和平均数≤几何平均数≤算术平均数≤平方平均数

1/((1/a+1/b)/2)<=sqrt(ab)<=(a+b)/2<=sqrt((a^2+b^2)/2) ,[(a>0,b>0)]

中位数：排序后，n为奇数，m=x(n/2),n为偶数，m=（x(n/2)+x(n/2+1))/2

众数：出现次数最多的值，可能零个，可能不止一个

最大值：max

最小值：min

四分位数：排序后，分别为Q1:x(n/4),Q2:x(n/2),Q3:x(n*3/4),用3个点分成4份,

排序后的最小估计值=Q1-k(Q3-Q1)

排序后的最大估计值=Q1+k(Q3-Q1)

k>1.5 中度异常值 k>3 极度异常值

四分位数的范围是Q1~Q3的范围

二、离散趋势

平均数为u,

方差：s=((x1-u)^2+(x2-u)^2+...+(xn-u)^2)/n

注：有些地方除数会用n-1，为了自由度

标准差：σ=sqrt(s)

平均差：su=(|x1-u|+|x2-u|+...+|xn-u|)/n

离散系数（也称变异系数）：Cv=σ/u(标准差/平均数)

三、分布状态（单峰分布即只有一个众数）

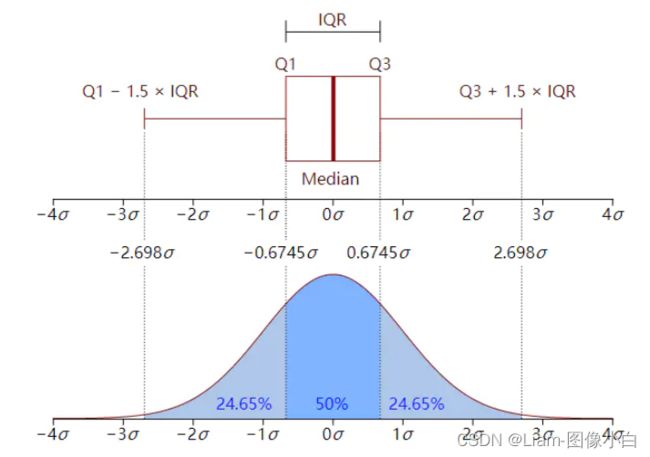
对称分布：平均值=中位数=众数，左右尾对称，又称U分布，概率

a、68.268949%的在平均数左右的一个标准差范围内，95.449974%在平均数左右两个标准差的范围内，99.730020%在平均数左右三个标准差的范围内，99.993666%在平均数左右四个标准差的范围内。

b、函数曲线的反曲点（inflection point）为离平均数一个标准差距离的位置

c、正态分布的概率密度曲线呈钟形，因此人们又经常称之为钟形曲线，面积为1，标准差越大，曲线高度越矮，标准差越小，曲线高度越高

d、标准正态分布是指u(平均值）为零，标准差（σ）为1的正太分布

右偏分布(skewed right)：正偏态

a、（左边的数据多），右尾长于左尾,，

b、平均数>中位数>众数

c、比较靠近第一分位数，远离第三分位数

左偏分布：负偏态

a、（右边的数据多），左尾长于右尾，平均数

b、平均数<中位数<众数

c、比较靠近第三分位数，远离第一分位数

偏态系数：SK= (均值一中位数)/标准差=（x-u)^3的求和/(σ*n)

注：还有这种计算

正态分布条件下，由于均值等于中位数，所以偏度系数等于0，

当偏态系数大于0时，则为正偏态；

当偏态系数小于0时，则为负偏态

偏态系数>1,严重右偏；>0.5,中度右偏

偏度度量：gi=K3/K2*sqrt(K2)

K2=((x1-u)^2+(x2-u)^2+...+(xn-u)^2)/n-1/12;

K3=n*(((x1-u)^3+(x2-u)^3+...+(xn-u)^3))/((n-1)*(n-2))

其中（-1/12）是归并矫正数，如计算过程中用组距时需要经过矫正，如果使用原始数据，则忽略

gi=0,对称，gi>0,正偏态（右偏），gi<0，负偏（左偏）

偏态分布的数据，有些可以通过变量代换变成正态分布

四、异常值

异常值：偏离大多数样本点的特殊值

判断异常值方法：箱线图法，正态分布法

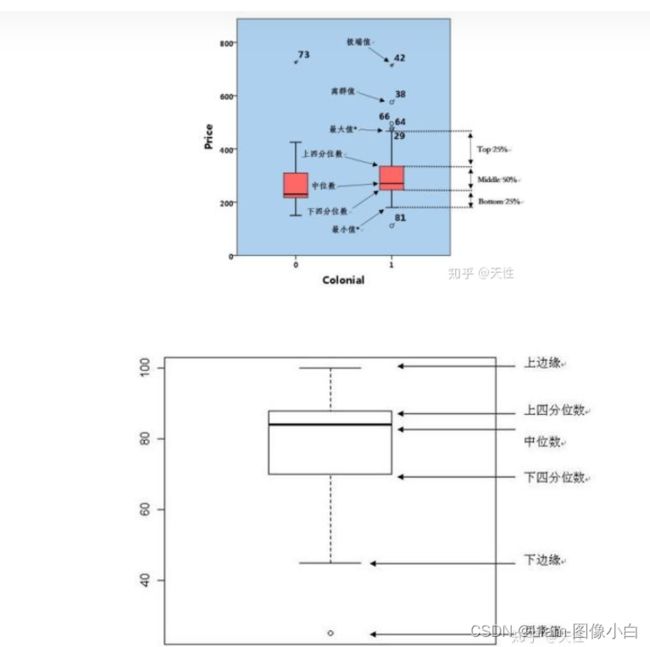
箱线图：

​

处理方法：修改（符号相反且不符合常理，eg：正数集合里的一个负数），删除（明显不符合统计类型，eg：年龄统计中出现的颜色），替换成平均数（极大值或极小值影响的一些统计）

五、数据拟合

最小二乘法：

直线方程的最小二乘法：

Ymean=k*Xmean+b

k=（(X1-Xmean)(Y1-Ymean)+(X2-Xmean)(Y2-Ymean)+...+(Xn-Xmean)(Yn-Ymean)）/((X1-Xmean)^2+(X2-Xmean)^2+...+(Xn-Xmean)^2）

b=Ymean-k*Xmean

相关关系：

按关系：正相关，负相关

按形式：线性相关，非线性相关

按变量数：单相关，复相关，偏相关（两个或以上变量，只关注一个变量，其他看作常量）

按程度：完全相关，不完全相关，完全不相关

相关系数：

k=Cov(X,Y）/(sqrt(var(X)*var(Y))

Cov(X,Y)是X，Y变量的协方差，Cov(X,Y)=EXY-EX*EY

Var(X)和Var(Y)是X和Y的方差

excel中相关系数的计算(和期望值计算稍有不同)

r=((X1-Xmean）(Y1-Ymean)+(X2-Xmean)(Y2-Ymean)+...+(Xn-Xmean)(Yn-Ymean))/sqrt((X1-Xmean)^2+(X2-Xmean)^2+...+(Xn-Xmean)^2)*sqrt((Y1-Ymean)^2+(Y2-Ymean)^2+...+(Yn-Ymean)^2)

|k|=1,完全相关，k=0,完全不相关，

注：印象中有此关系，|k|<0.3,基本不相关，|k|>0.8,高度相关，0.3<|k|<0.5,低度相关，0.5<|k|<0.8中度相关，

六、数据分析

一、明确问题：明确分析数据的真实需求

二、理解数据：数据获取和数据探索，包含数据采集，数据抽样，数据认知

三、数据清洗：纠正数据文件中可识别的错误，检查数据一致性，处理无效值和缺失值，和异常值

四、统计分析和可视化：将清洗后的数据以可视化的方式展示

五、结论和建议：对结果进行解读，得出有价值的结论并给出相关建议

---

总结

来源各种百度及以前的笔记，有些地方感觉描述不清，例如偏态系数和偏度度量相关，但是自己忘记相关的统计学知识了，还有最小二乘法以及相应的残差计算，和百度的内容有些差异，对数学符号已经忘的差不多了，如果遇到了更标准的描述，或者理解清晰了，再更新，部分图直接来源其他作者，但是自己忘记当时从哪下载的了