多目标线性规划——pulp
一、背景
因为工作原因需要了解一些运筹优化相关的算法,所以在同事的介绍下找了《运筹学导论(第10版)》(Introduction to Operations Research)看。最近又在微信群中看到有些同学在讨论,于是乎便把用到的相关工具,以及简单用法做一些记录。(后续可能还会逐步更新)
二、多目标优化问题
优化目标1: m a x x 1 , x 2 2 x 1 + 3 x 2 max_{x_1,x_2} \ 2x_1 + 3x_2 maxx1,x2 2x1+3x2
优化目标2: m a x x 1 , x 2 4 x 1 − 2 x 2 max_{x_1,x_2} \ 4x_1 - 2x_2 maxx1,x2 4x1−2x2
约束:s.t.
x 1 + x 2 ≤ 10 2 x 1 + x 2 ≤ 15 x 1 , x 2 ≥ 0 x_1 + x_2 \le 10 \\ 2x_1 + x_2 \le 15 \\ x_1, x_2 \ge 0 x1+x2≤102x1+x2≤15x1,x2≥0
三、解
3.1 Pulp包解
3.1.1 两步解
最大化一个目标,然后将其添加为约束并解决另一个目标
import pulp
from pulp import LpVariable, LpProblem, LpMaximize
# 最大化一个目标,然后将其添加为约束并解决另一个目标
linear_prob = LpProblem('为第一目标最大化', LpMaximize)
# variable
x1 = LpVariable('x1', lowBound=0)
x2 = LpVariable('x2', lowBound=0)
# max_target
linear_prob += 2*x1 + 3*x2
# s.t.
linear_prob += x1 + x2 <= 10
linear_prob += 2 * x1 + x2 <= 15
# solve
solution = linear_prob.solve()
print('Obj: {Obj}; \nmax = {max_} \nSolution: x1={x1} x2={x2}'.format(
Obj = linear_prob.objective,
max_=pulp.value(linear_prob.objective),
x1 = pulp.value(x1),
x2 = pulp.value(x2)
)
)
"""
Obj: 2*x1 + 3*x2;
max = 30.0
Solution: x1=0.0 x2=10.0
"""
基于第一个解,将其作为限制解决第二个目标
linear_prob_sec = LpProblem('为第二目标最大化', LpMaximize)
# max_target
linear_prob_sec += 4*x1 - 2*x2
# s.t.
linear_prob_sec += x1 + x2 <= 10
linear_prob_sec += 2 * x1 + x2 <= 15
linear_prob_sec += 2*x1 + 3*x2 >= 30
# solve
solution = linear_prob_sec.solve()
print('Obj: {Obj}; \nmax = {max_}\nSolution: x1={x1} x2={x2}'.format(
Obj = linear_prob_sec.objective,
max_=pulp.value(linear_prob_sec.objective),
x1 = pulp.value(x1),
x2 = pulp.value(x2)
)
)
"""
Obj: 4*x1 - 2*x2;
max = -19.999999999995993
Solution: x1=1.0018653e-12 x2=10.0
"""
3.1.2 使用采样的权重和具有定义步长的迭代组合目标
现在的问题是如何选择α。
在这种情况下,典型的方法是确定有效边界。在经济学中,例如被称为“最佳最优”。
问题重构
优化目标: m a x x 1 , x 2 α ( 2 x 1 + 3 x 2 ) + ( 1 − α ) ( 4 x 1 − 2 x 2 ) max_{x_1,x_2} \ \alpha(2x_1 + 3x_2) + (1-\alpha)(4x_1 - 2x_2) maxx1,x2 α(2x1+3x2)+(1−α)(4x1−2x2)
约束:s.t.
x 1 + x 2 ≤ 10 2 x 1 + x 2 ≤ 15 x 1 , x 2 ≥ 0 x_1 + x_2 \le 10 \\ 2x_1 + x_2 \le 15 \\ x_1, x_2 \ge 0 x1+x2≤102x1+x2≤15x1,x2≥0
import matplotlib.pyplot as plt
import pulp
from pulp import LpVariable, LpProblem, LpMaximize
import numpy as np
import pandas as pd
plt.style.use('ggplot')
x1 = LpVariable('x1', lowBound=0)
x2 = LpVariable('x2', lowBound=0)
step_size = 0.01
sove_df = pd.DataFrame(columns=['alpha', 'x1', 'x2', 'obj_v', 'org_v'])
for i in range(0, 101, int(step_size * 100)):
lp = LpProblem('多目标优化', LpMaximize)
# obj
lp += (i/100)*(2*x1 + 3*x2) + (1 - i/100)*(4*x1 - 2*x2)
# s.t.
lp += x1 + x2 <= 10
lp += 2 * x1 + x2 <= 15
res = lp.solve()
x1_, x2_ = pulp.value(x1), pulp.value(x2)
org_v = (2*x1_ + 3*x2_) + (4*x1_ - 2*x2_)
sove_df.loc[int(i/(step_size*100))] = [i/100, x1_, x2_, pulp.value(lp.objective), org_v]
sv_max = sove_df['obj_v'].max()
sv_min = sove_df['obj_v'].min()
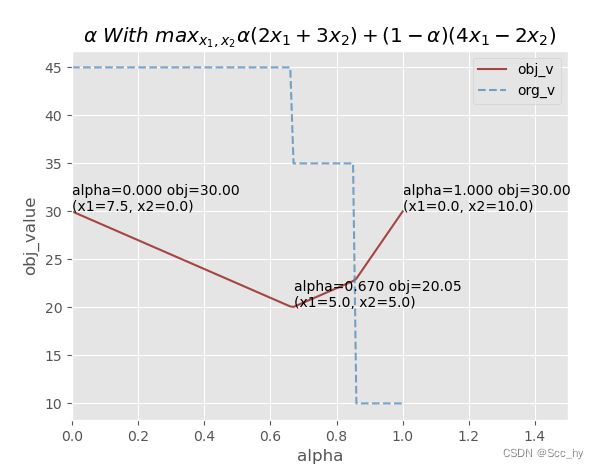
plt.title('$ \\alpha \ With \ max_{x_1,x_2} \\alpha(2x_1 + 3x_2) + (1-\\alpha)(4x_1 - 2x_2)$')
plt.plot(sove_df["alpha"], sove_df["obj_v"],color="darkred", alpha=0.7, label="obj_v")
for idx, row in sove_df[sove_df['obj_v']==sv_max].iterrows():
plt.text(row.alpha, row.obj_v, f'alpha={row.alpha:.3f} obj={row.obj_v:.2f}\n(x1={row.x1}, x2={row.x2})')
for idx, row in sove_df[sove_df['obj_v']==sv_min].iterrows():
plt.text(row.alpha, row.obj_v, f'alpha={row.alpha:.3f} obj={row.obj_v:.2f}\n(x1={row.x1}, x2={row.x2})')
plt.plot(sove_df["alpha"], sove_df["org_v"],color="steelblue", alpha=0.7, linestyle='--', label="org_v")
# plt.ylim(15, 35)
plt.xlim(0, 1.5)
plt.legend()
plt.xlabel("alpha", size=12)
plt.ylabel("obj_value", size=12)
plt.show()