【传统机器学习算法—笔记】-线性回归
版权声明:如果对大家有帮助,大家可以自行转载的。原文链接:
监督学习分为:
回归——预测出的标签连续(房价、股票预测);
分类——预测出的标签离散。
线性回归
是一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值和真实值之间的误差最小化。
线性回归的符号约定
x和y的关系
h(x) = w0+w1x1+…+wnxn
可以设x0=1,则:
h(x) = w0x0+w1x1+w2x2+…+wnxn = wTx(w0为偏置项)——机器学习中默认向量为列向量
损失函数(loss function)
度量单样本预测的错误程度,损失函数值越小,模型越好。常用的损失函数包括:
0-1损失函数:0-1损失是指预测值和目标值不相等为1, 否则为0:

特点:
(1)0-1损失函数直接对应分类判断错误的个数,但是它是一个非凸函数,不太适用.
(2)感知机就是用的这种损失函数。但是相等这个条件太过严格,因此可以放宽条件,即满足 |Y-f(x)|,T时认为相等,

平方损失函数(常用):平方损失函数标准形式如下:
特点:经常应用与回归问题
绝对值损失函数:绝对值损失函数是计算预测值与目标值的差的绝对值:![]()
对数损失函数:log对数损失函数的标准形式如下:![]()
特点:
(1) log对数损失函数能非常好的表征概率分布,在很多场景尤其是多分类,如果需要知道结果属于每个类别的置信度,那它非常适合。
(2)健壮性不强,相比于hinge loss对噪声更敏感。
(3)逻辑回归的损失函数就是log对数损失函数。
指数损失函数:
![]()
特点:对离群点、噪声非常敏感。经常用在AdaBoost算法中。
Hinge损失函数:
![]()
代价函数
度量全部样本集的平均误差。常用的代价函数包括均方误差、均方根误差、平均绝对误差等。
最小二乘法
要找到一组w(w0,w1,w2…wn),使得J(w)的残差平方和最小,即最小化。 (J(w)为代价函数)
J ( w ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J\left( w \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}} J(w)=2m1i=1∑m(h(x(i))−y(i))2
其中: h ( x ) = w T X = w 0 x 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n {h}\left( x \right)={w^{T}}X={w_{0}}{x_{0}}+{w_{1}}{x_{1}}+{w_{2}}{x_{2}}+...+{w_{n}}{x_{n}} h(x)=wTX=w0x0+w1x1+w2x2+...+wnxn
将向量表达形式转为矩阵表达形式,则有 J ( w ) = 1 2 ( X w − y ) 2 J(w )=\frac{1}{2}{{\left( Xw -y\right)}^{2}} J(w)=21(Xw−y)2 ,其中 X X X为 m m m行 n + 1 n+1 n+1列的矩阵( m m m为样本个数, n n n为特征个数), w w w为 n + 1 n+1 n+1行1列的矩阵(包含了 w 0 w_0 w0), y y y为 m m m行1列的矩阵,则可以求得最优参数 w ∗ = ( X T X ) − 1 X T y w^{*} ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y w∗=(XTX)−1XTy
梯度下降
中心思想:迭代的调整参数从而使成本函数最小化。
梯度下降有三种形式,分别为:
批量梯度下降(BGD):梯度下降的每一步中,都用到了所有的训练样本;
wj是其中的一个参数,
随机梯度下降(SGD):梯度下降的每一步中,用到一个样本,在每一次计算后便更新参数,而不需要首先将所有的训练集求和;
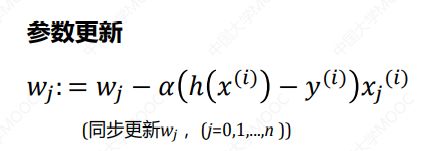
小批量梯度下降(MBGD):梯度下降的每一步中,用到了一定批量的训练样本。

b=1 随机梯度下降
b=m 批量梯度下降
b=batch_size 小批量梯度下降,batch_size通常是2的指数倍,常见有32,64,128等。
梯度下降与最小二乘法比较
梯度下降:需要选择学习率 α \alpha α,需要多次迭代,当特征数量 n n n大时也能较好适用,适用于各种类型的模型
最小二乘法:不需要选择学习率 α \alpha α,一次计算得出,需要计算 ( X T X ) − 1 {{\left( {{X}^{T}}X \right)}^{-1}} (XTX)−1,如果特征数量 n n n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O(n^3) O(n3),通常来说当 n n n小于10000 时还是可以接受的,只适用于线性模型,不适合逻辑回归模型等其他模型
数据归一化/标注划 (解决特征尺度不一致)
为什么要标准化归一化?
提升模型精度:不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
加速模型收敛:最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。
归一化(最大-最小规范化)

将数据映射到[0,1]区间,归一化的目的是使得各特征对目标变量的影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
Z-Score标准化

处理后的数据均值为0,方差为1,标准化为了不同特征之间具备可比性,经过标准化变换之后的特征分布没有发生改变,就是当数据特征取值范围或单位差异性较大时,最好是做一下标准化处理。
需要做数据归一化/标准化的情形:线性模型,如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。另外,线性回归类的几个模型一般情况下也是需要做数据归一化标准化处理的。
不需要做数据归一化/标准化的情形:决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感,如随机森林、XGboost、Light GBM等树模型,以及朴素贝叶斯,以上这些模型一般不需要做数据归一化/标准化处理。
过拟合的处理:
- 获得更多的训练数据:使用更多的训练数据是解决过拟合问题最有效的手段,因为更多的样本能够让模型学习到更多更有效地特征,减少噪声的影响。
- 降维:即丢弃一些不能帮助我们正确预测的特征,可以是手工保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)。
- 正则化:保留所有的特征,但是减少参数的大小,它可以改善或者减少过拟合问题。
- 集成学习方法:集成学习是把多个模型集成在一起,来降低单一模型的过拟合风险。
欠拟合的处理:
- 添加新特征:当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。通过挖掘组合特征等新的特征,往往能够取得更好的效果。
- 增加模型复杂度:简单模型的学习能力较差,通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如,在线性模型中添加高次项,在神经网络中增加网络层数或神经元个数等。
- 减少正则化系数:正则化是用来放置过拟合的,但当模型出现欠拟合现象时,则需要有针对性地减小正则化系数。
正则化
L1正则化: J ( w ) = 1 2 ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n ∣ w j ∣ J ( {w } ) = \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } ( h _ { w} ( x ^ { ( i ) } ) - y ^ { ( i ) } ) ^ { 2 } + \lambda \sum _ { j = 1 } ^ { n } | w _ { j } | J(w)=21∑i=1m(hw(x(i))−y(i))2+λ∑j=1n∣wj∣,此时称作`Lasso回归。
L2正则化: J ( w ) = 1 2 ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n w j 2 J ( {w } ) = \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } ( h _ { w} ( x ^ { ( i ) } ) - y ^ { ( i ) } ) ^ { 2 } + \lambda \sum _{ j = 1 } ^ { n } w _ { j } ^2 J(w)=21∑i=1m(hw(x(i))−y(i))2+λ∑j=1nwj2,此时称作岭回归 。
Elastic Net: J ( w ) = 1 2 ∑ i = 1 m ( h w ( x ( i ) ) − y ( i ) ) 2 + λ ( p . ∑ j = 1 n ∣ w j ∣ = J ( {w } ) = \frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } ( h _ { w} ( x ^ { ( i ) } ) - y ^ { ( i ) } ) ^ { 2 } + \lambda (p.\sum _{ j = 1 } ^ { n }| w _ { j } |= J(w)=21∑i=1m(hw(x(i))−y(i))2+λ(p.∑j=1n∣wj∣=,此时称作弹性网络。
其中 λ \lambda λ为正则化系数,调整正则化项与训练误差的比例, λ \lambda λ>0。
1>=p>=0为比例系数,调整L1正则化与L2正则化的比例。
