数据分析-分类评价-PR与ROC曲线
目录
前言
一、PR曲线
1.引入库
2.计算概率值
3.计算不同阈值的precision,recall
4.绘制P-R曲线
二、ROC曲线
1.引入库
2.计算慨率
3、计算不同阈值的fpr,tpr
4.绘制曲线
5.计算AUC
前言
分类模型的评价通常可以使用正确率、F1、精确率、召回率等指标来评价。sklearn提供以下包来实现相应的指标计算。
metrics.confusion_matrix 输出混淆矩阵 (通常1类为正类,0类为负类)
| Confusion Matrix |
预测标签 |
||
| 1 |
0 |
||
| 真实标签 |
1 |
TP(真1类样本数量) |
FN(假0类样本数量) |
| 0 |
FP(假1类样本数量) |
TN(真0类样本数量) |
|
metrics.accuracy_score 计算正确率
正确率() = ( + )/( + + + )
metrics.recall_score 计算召回率
1类的召回率() = /( + )
metrics.precision_score 计算精确率
1类的精确率() = /( + )
metrics.f1_score 计算F1 值
1类的1 = 2 × 精确率 × 召回率 /(精确率 + 召回率)
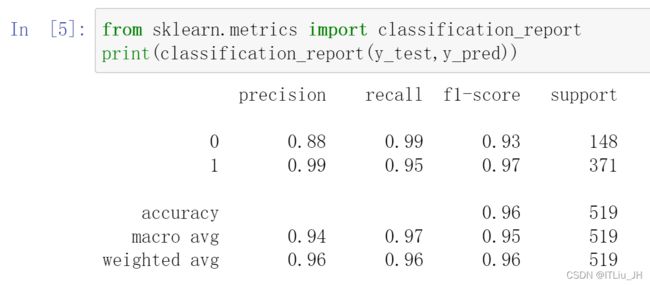
metrics.classification_report 输出分类指标的文本报告 ,其中macro avg简单的求两类指标的平均值,weighted avg考虑样本的不均衡,对样本数多的类别给了更大的权重。
但算法对样本进行分类时,样本并不是绝对的1、0类,都是多大的概率是1或是0类。通常先设定好样本类别的阈值,当该样本是1样本的概率大于阈值时,输出样本为1类,否则为0类。比如阈值为50%,当70%的概率认为样本A是1类,输出样本A为1类。20%的概率认为样本B是1类,输出B为0类。
一、PR曲线
调整阈值可以得到不同的样本类别的不同划分,由此每一个不同的阈值,都可以计算对应的precision和recall,那么就可以按阈值排列顺序,绘制PR曲线。通常在曲线上找到平衡点 ( BEP) ,即“查准率(精确率)=查全率(召回率)”时的阈值取值,作为最佳的阈值;但在类别错误代价不同时可能更看重“查准率”(误判为1类的代价高)或“查全率”(误判为0类的代价高)。
1类召回率(recall)=TP/(TP+FN)
1类精确率(precision)=TP/(TP+FP)
1.引入库
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
2.计算概率值
probs = clf.predict_proba(test_x)
#probs包含样本属于0类与1类的概率值
#取样本属于1类的概率值
probs=probs[:,1]3.计算不同阈值的precision,recall
precision,recall,thresholds = precision_recall_curve(test_y,probs,pos_label=1)
计算1类的精度与召回率随阈值的变化,也可计算0类的精度与召回率随阈值的变化。
4.绘制P-R曲线
plt.plot(recall, precision)
plt.title('P-R曲线')
plt.xlabel('召回率')
plt.ylabel('精确率')二、ROC曲线
ROC 全称是"受试者工作特征" (Receiver Operating Characteristic),考察模型在“一般情况下”的预测能力。横轴为,纵轴为,曲线越靠近(0, 1)证明模型整体预测能力越强。
TPR(真1类)=TP/(TP+FN)
FPR(假1类)=FP/(TN+FP)
首先,将测试集样本的预测概率从大到小排列;然后,将每个预测概率作为分类阈值,计算在此阈值下的一组TPR和FPR;最后,使FPR为横轴, TPR为纵轴,按阈值排列顺序,绘制ROC曲线。
1.引入库
from sklearn.metrics import roc_curve
2.计算慨率
probs = clf.predict_proba(test_x)
#probs包含样本属于0类与1类的概率值
#取样本属于1类的的概率
probs=probs[:,1]3、计算不同阈值的fpr,tpr
fpr,tpr,thresholds = roc_curve(test_y,probs)4.绘制曲线
plt.plot(fpr, tpr)
plt.xlabel('假正率') #设定1类为正
plt.ylabel('真正率')
plt.title('ROC曲线')
5.计算AUC
ROC曲线与横轴之间的面积为AUC,取值为[0.5, 1],其数值越大证明模型整体预测能力越强。当AUC=0.5时预测结果等同于随机猜测,小于0.5基本不可能,如果小于0.5表明模型的结果比随机猜测还要差。
from sklearn.metrics import roc_auc_score
roc_auc_score(test_y,probs)
#or
from sklearn import metrics
metrics.auc(fpr,tpr)