ARIMA模型时间序列数据分析（附python代码）

ARIMA模型建模流程 

建模流程

1）平稳性检验与差分处理

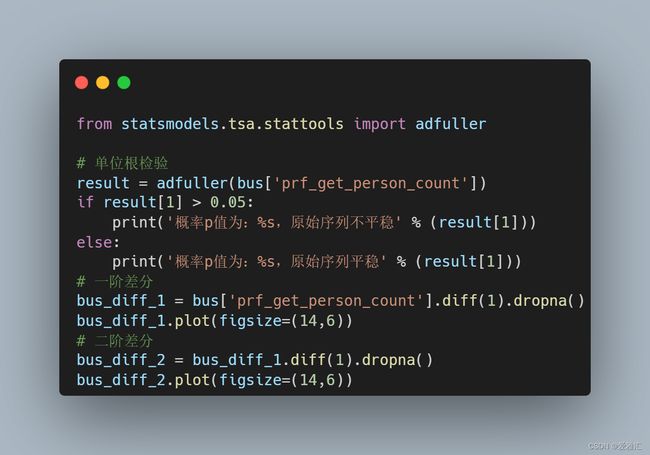
我们选取原始数据bus中的“prf_get_person_count”列，并截取前32个站点的数据进行平稳性检验，这里采用的是ADF检验确定数据的平稳性，导入statsmodels包下的adfuller函数，该函数返回adf值与概率p值。若原始序列不平稳，就进行差分处理，并对一阶差分序列再次进行ADF检验，直至序列平稳，进行后续分析。

2）白噪声检验

白噪声数据没有分析价值，所以要进行白噪声检验，LB检验可以确定数据是否为白噪声，这里导入的是statsmodels包下的acorr_ljungbox函数。

3）模型定阶

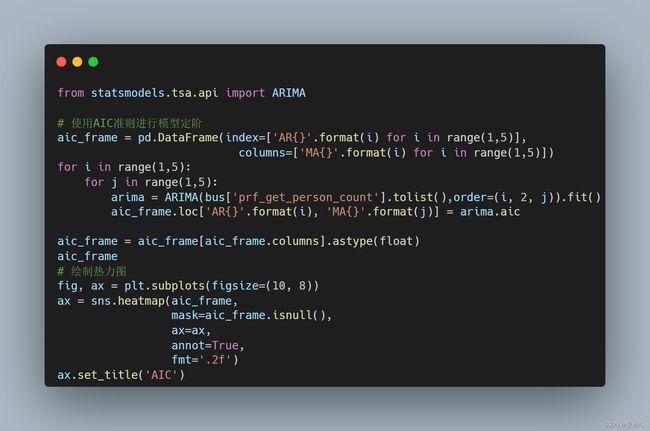
使用AIC准则进行模型参数估计与模型定阶，这里通过绘制AIC数据表aic_frame以及其对应的热力图来直观地找出AIC值最小时对应的ARIMA(p,d,q)中的p、q值，从而确定模型。

4）预测

model1对应ARIMA(4,2,3)，其AIC值最小；model2对应ARIMA(3,2,1)，其AIC值最大。选取两个模型进行对比分析。

output1和output2为预测值，通过绘制原始数据与预测数据图，可以直观地感受模型的拟合效果。

5）模型检验

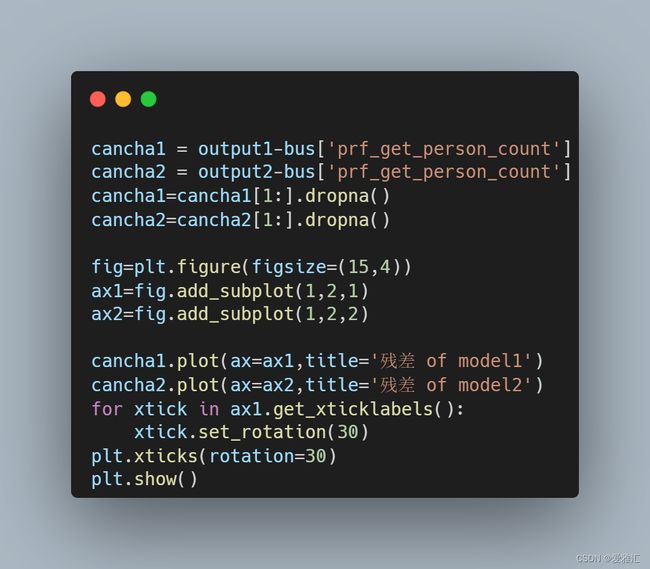
首先绘制残差图，观察残差序列中是否有明显的趋势性或者季节性特征。

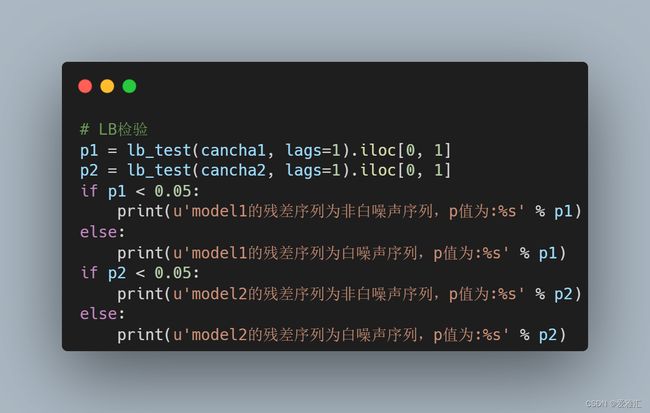
使用LB检验残差序列是否为白噪声，若是白噪声，则模型性能较好，反之则差。

通过绘制残差序列直方图密度图和QQ图来对残差序列进行正态性检验，残差序列越接近正态分布，模型的性能就越好。

结果分析

1）平稳性检验与差分处理结果

原始数据（左）与单条路线数据（右）

原始数据单位根检验结果为p=0.70，远高于0.05，认为序列中存在单位根，即原始序列不平稳。对数据进行一阶差分后结果如左图所示，其单位根检验结果为0.94，一阶差分序列不平稳。对数据进行二阶差分后结果如右图所示，其单位根检验结果为0.034，认为二阶差分序列满足平稳性要求，即后续建模过程中ARIMA(p,d,q)中的d选择2。

一阶差分序列（上）与二阶差分序列（下）

2）白噪声检验结果

LB检验的概率p值为0.0106，认为该时间序列为非白噪声序列，可以进行后续分析。

3）模型定阶结果

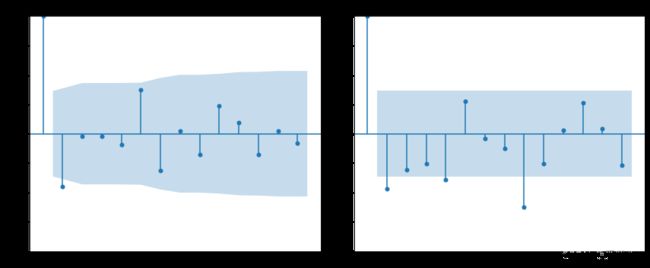
绘制二阶差分序列的ACF与PACF图，均表现出明显的拖尾。

ACF图（左）与PACF图（右）

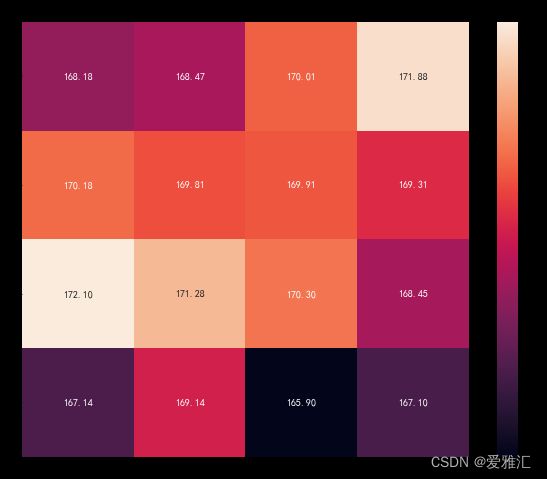
根据AIC准则，绘制热力图如下，可以看出，AIC最小值与最大值对应的参数分别为p=4，q=3和p=3，q=1，故我们选择ARIMA(4,2,3)作为model1，选择ARIMA(3,2,1)作为model2，对比分析两个模型对数据的拟合效果。

AIC值热力图

4）预测结果

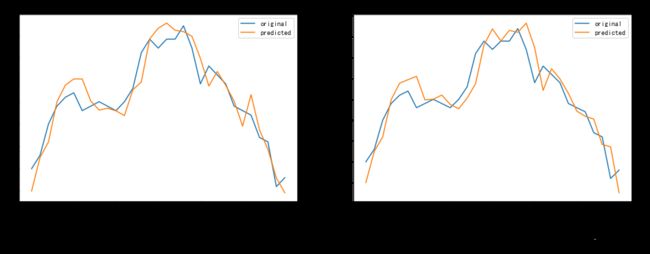
分别绘制model1与model2的预测图如图所示：

model1（左）与model2（右）真实值与预测值对比图

5）模型检验结果

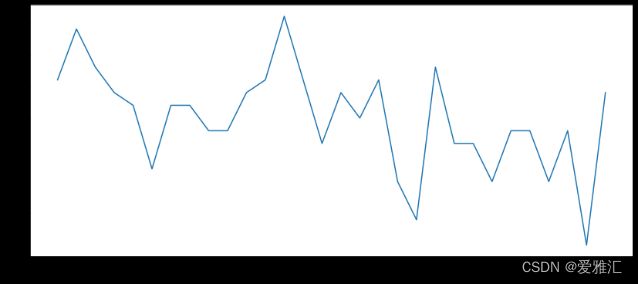
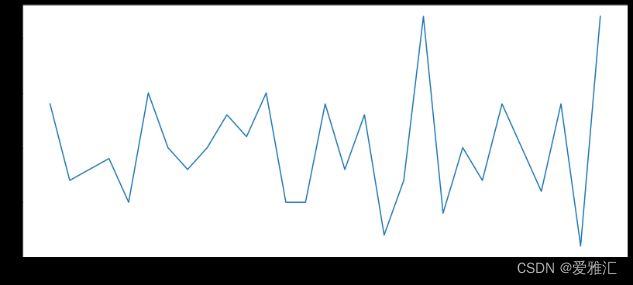
首先绘制model1和model2的残差序列图，观察其是否具有明显的趋势性和季节性特征，为后续检验做准备。

model1（左）与model2（右）残差序列图

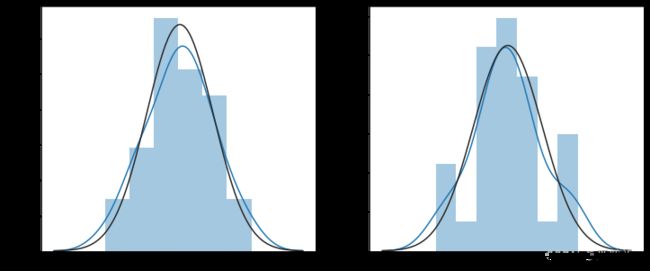
       绘制残差序列的直方图密度图，可以看出model1与model2均大致服从正态分布，且model1的正态性更明显。

model1（左）与model2（右）残差序列直方图密度图

        绘制残差序列的QQ图，可以看出，两个图均表现出中间密两头疏和大致为一条直线的特点，且model1明显优于model2。

model1（左）与model2（右）残差序列QQ图

对残差序列进行白噪声检验，得到model1和model2的残差序列LB检验的概率p值分别为0.8和0.676，可以认为两个模型的残差序列均为白噪声序列，且model1的性能略高于model2，与前面的AIC值相符合。

ARIMA模型特点：

优点：模型简单，易于解释；可以通过差分处理非平稳时间序列。

缺点：只适用于短期预测，长期预测准确度较低。

python代码：

https://download.csdn.net/download/m0_48973594/85800180https://download.csdn.net/download/m0_48973594/85800180