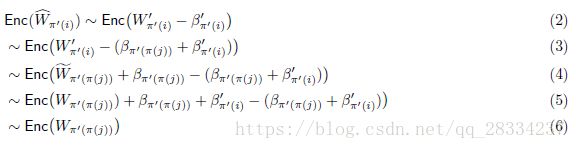斌斌有礼吗

Top-k Query Processing on Encrypted Databases with Strong Security Guarantees

摘要

外包云数据库中的隐私问题最近变得越来越重要，并且已经提出了许多关于加密数据的高效且可扩展的查询处理方法。但是，如何安全地处理云中加密数据库的top-k排名查询的工作非常有限。在本文中，我们专注于这个问题：对外包数据库的top-k查询进行安全和高效的处理。特别是，我们提出了第一个有效且可证明的安全top-k查询处理结构，它实现了自适应CQA安全性。我们开发了一个名为EHL的加密数据结构，并在我们的安全模型下描述了几个安全子协议，以回答top-k查询。此外，我们针对空间和时间效率优化了查询算法。最后，在实验中，我们使用真实世界数据集对我们的协议进行了实证分析，并证明了我们的构造是有效和实用的。

1.简介

随着远程存储和云计算服务的出现，例如亚马逊的EC2，谷歌AppEngine和微软的Azure，许多企业，组织和终端用户可能会将他们的数据外包给那些云服务提供商，以实现可靠的维护，更低的成本和更好的性能。事实上，最近开发了云上的许多数据库系统，以较低的成本提供高可用性和灵活性。然而，尽管有这些好处，但仍有许多原因使许多用户不使用这些服务，尤其是那些拥有敏感和有价值数据的用户。毫无疑问，这方面的主要问题与安全和隐私问题有关[3]。实际上，数据所有者和客户可能不完全信任公共云，因为一些黑客或具有root权限的云管理员可以出于任何目的完全访问所有数据。有时，云提供商可能会将其业务出售给不受信任的公司，该公司将拥有对数据的完全访问权限。解决这些问题的一种方法是在将数据外包到云之前加密数据。例如，电子健康记录（EHR）应在外包之前加密，符合HIPAA1等法规。加密数据可以为Database-As-Service环境带来增强的安全性[25]。然而，它也在查询和计算这些数据时带来了重要的困难。

虽然top-k查询是许多数据库应用程序中的重要查询类型[28]，但据我们所知，现有的工作都没有安全有效地处理top-k查询。 Vaiyda等人 [46]研究了保护隐私的top-k查询，其中数据被垂直分区而不是加密数据。黄等人 [48]提出了一种针对knn查询的加密方案，并提到了一种转换其方案以解决top-k查询的方法，但是，如[50]所示，它们的加密方案不安全，易受所选择的明文攻击。

我们假设数据所有者和客户端是可信的，但云服务器不可信。因此，数据所有者在将其外包到云之前使用一些概率加密方案(每次加密首先选择一个随机数再生成密文，故同一个明文产生加密后的结果是不同的）来加密每个数据库关系R. 授权用户指定查询q并生成令牌（token)以查询服务器。我们的目标是允许云基于R上的用户定义排名函数安全地计算前k个结果，更重要的是，云不应该学习任何有关R或q的内容。考虑以下健康医疗数据库的真实示例：

例1.1。授权医生Alice希望根据加密电子健康记录数据库患者的一些排名标准获得前k个结果（见表1）。加密的患者数据库可能包含几个属性; 这里我们只列出表1中的一些：患者姓名，年龄，身份证号码，trestbps ，chol，thalach。

top-k查询的一个示例（以SQL查询的形式）可以是：

SELECT * FROM patients ORDERED BY chol + thalach STOP after k。

也就是说，医生希望根据所有患者记录中的得分chol + thalach得到前2个结果。但是，由于此表包含有关患者的非常敏感的信息，因此数据所有者首先加密表，然后将其委派给云。因此，Alice从数据所有者请求密钥并基于该查询生成查询令牌。然后，云搜索并计算加密表以找出前k个结果。在这种情况下，前2名结果是患者David和Emma的记录。

我们的协议扩展了非随机访问（NRA）[22]算法，用于在概率加密的关系数据库上计算top-k查询。此外，我们的查询处理模型假设两个非串联的半诚实云，这是已经被证明运行良好的模型（见[21,12,36,7,11]）。我们对数据库进行加密，使服务器可以在加密数据库上无意识地/(obliviously)执行NRA而无需了解底层数据。这是在辅助独立云服务器（或Crypto Cloud）的帮助下完成的。但是，加密数据库仅存储在主云中。我们采用两种高效的现有安全协议，EncSort [7]和EncCompare [11]，这是我们在top-k安全构建中需要的两个构建块。我们选择这两个构建块主要是因为它们的效率。

在查询处理期间，我们提出了几个新的子例程，它们可以安全地计算最佳/最差分数，并在加密数据库上重复删除复制数据项（de-duplicate replicated data items）。请注意，我们提出的子协议也可以用作其他应用程序的独立构建块。我们还想指出，在查询阶段，客户端执行的计算非常少。客户端只需要为服务器计算一个简单的令牌，所有相对较重的计算都由云端执行。此外，我们还探讨了多个加密关系的top-k连接查询问题。

我们还设计了一个安全的top-k连接运算符，表示为 $\bowtie$ sec，以基于等连接条件安全地连接表。云同态地计算联接结果顶部的top-k连接并报告加密的top-k结果。下面我们总结一下我们的主要贡献：

我们提出了一种新的实用协议，旨在通过加密的关系数据库回答top-k查询。
我们提出了两种称为EHL和EHL+的加密数据结构，它们允许服务器同态地评估两个对象之间的相等关系。
我们提出了几个独立的子协议，使得云可以安全地计算最佳/最差分数，并使用另一个非共谋服务器去重复删除复制的加密对象。
我们还扩展了我们的技术，以解决多个加密关系的top-k连接查询。
该方案使用真实数据集进行实验评估，结果表明我们的方案是有效和实用的

2.相关工作和背景

处理外包加密数据库查询的问题并不新鲜。工作[25]建议使用bucketization在数据库服务提供者模型中对加密数据执行SQL查询。从那时起，在对加密数据执行各种查询时出现了许多工作。与top-k查询相关的一个相关问题是kNN（k最近邻）查询。请注意，不应将top-k查询与相似性搜索混淆，例如kNN查询。对于kNN查询，人们有兴趣通过数据库检索k个最相似的对象到查询对象，其中在一些度量空间上测量两个对象之间的相似性，例如L2度量。已经提出许多工作来专门处理对加密数据的kNN查询，例如[48,21,50,15]。隐私保护关键字搜索查询或布尔查询（例如[44,17,13]）已经完成了大量工作。最近的工作[42]提出了对加密数据的析取正规形式查询的布尔查询的通用框架。此外，已经提出了许多范围查询的工作[43,27,33]。其他相关工作包括隐私保护数据挖掘[2,30,47,35,37]。

密码学社区最近的工作表明，可以使用完全同态加密（FHE）[23]或遗忘RAM [24]对加密数据执行任意计算。然而，这种结构的性能开销在实践中非常高，因此它们不适合于实际的数据库查询。 ORAM方案[41]的一些最新进展显示出前景，并且可能在某些环境中使用。如上所述，[46]是研究隐私保护top-k查询执行的唯一工作。但是，他们的方法主要是基于k-匿名隐私策略，因此，它无法扩展到加密数据库。最近，差异隐私[20]已成为一种强大的模型，可以保证概率准确性，防范未知对手。但是，这里我们考虑外包模型中的加密数据;而且，我们不希望我们的查询答案被噪声扰乱，但我们希望我们的查询结果是准确的。 Kuzu等人 [32]提出了一种方案，利用DP并泄漏混淆的访问统计数据，以实现高效的搜索。已经广泛研究的另一种方法是保留顺序的加密（OPE）[2,4,9,40,35]，它保留了消息的顺序。我们注意到，通过定义，OPE直接揭示了对象排名的顺序，因此不能满足我们的数据隐私保证。此外，[26]提出了一种使用确定性代理加密的访问控制原型，并且已经通过使用嵌入式安全硬件提出了其他安全数据库系统，例如TrustedDB [6]和Cipherbase [5]。

3.前期工作

3.1问题定义

考虑这个数据拥有者具有n个对象的数据库关系R，n个对象用o1,...,on表示，每个对象oi都有M个属性。为简单起见，我们假设所有M属性都采用数值。因此，关系R是n*M矩阵。数据所有者希望将R外包给完全不受信任的第三方云S1。因此，数据所有者加密R并将加密的关系ER发送到云。之后，任何授权客户端都应该能够通过在M（加密）属性上指定k和得分函数，直接从S1获得关于此加密关系的top-k查询的结果。我们认为单调评分（排名）函数是所有属性的加权线性组合，即 $F_{w}(o) =\sum w_{i}\times x_{i}(o)$ ，每个 $w_{i}\geq 0$ 是第i个属性的用户指定权重， $x_{i}(o)$ 是对象o的第i个属性的局部得分（值）。注意，我们考虑单调线性函数主要是因为它是top-k查询中最重要和最广泛使用的得分函数[28]。 top-k查询的结果是具有最高k个 $F_{w}$ 值分数的对象。例如，考虑想要在加密关系ER上运行top-k查询的授权客户Alice。考虑以下查询：q = SELECT * FROM ER ORDER BY $F_{w}(\cdot )$ STOP after k;也就是说，对于指定的一组权重Alice希望根据她的评分函数 $F_{w}$ 获得前k个结果。 Alice首先必须从数据所有者请求密钥，然后生成查询令牌tk。 Alice将tk发送到云服务器。存储加密数据库ER的云服务器处理top-k查询并将加密结果发送回Alice。在现实世界场景中，授权客户端可以在本地存储用于生成令牌的密钥。

3.2架构

我们考虑在半诚实（或诚实但好奇）的对抗模型下对云进行安全计算。此外，我们的模型假设存在两个不同的非串联半诚实云提供商S1和S2，其中S1存储加密数据库ER，S2保存密钥并提供加密服务。我们将服务器S2称为加密云，并假设S2驻留在云环境中并与S1隔离。双方S1和S2彼此不信任，因此，他们必须对加密数据执行安全计算。双方S1和S2属于两个不同的云提供商，互不信任;因此，他们必须对加密数据执行安全计算。事实上，加密云已经在今天的一些工业应用中被构建和使用（例如，pCloud Crypto5或boxcryptor6）。该模型并不是新的，已经广泛用于相关工作，如[21,12,36,7,11]。正如这些工作所指出的，我们强调这些云服务通常由一些大型公司提供，例如亚马逊，微软Azure和谷歌，他们也有商业利益，不要串通。 Crypto Cloud S2配备了加密处理器，用于存储解密密钥。这种假设背后的直觉如下。市场上的大多数云服务提供商都是成熟的IT公司，例如Amazon AWS，Microsoft Azure和Google Cloud。因此，他们之间的勾结是不太可能的，因为它会损害他们的声誉，从而影响他们的收入。当服务器S1接收到查询令牌时，S1用Crypto Cloud S2发起安全计算协议。图1显示了该体系结构的概述。

3.3加密工具

在表2中，我们总结了符号。在下文中，我们将介绍我们构造中使用的加密原语。

Paillier Cryptosystem Paillier密码系统[38]是一种语义安全的公钥加密方案。用于加密的消息空间M是 $Z_{N}$ ，其中N是两个大素数p和q的乘积。对于一个消息 $m\in Z_{N}$ ，我们将公钥pk加密过的消息表示为： $E_{nc_{pk}}(n)\in Z_{N^{2}}$ 。当密钥在文本中清楚时，我们简单地使用 $E_{nc}(m)$ 来表示加密的m， $D_{ec_{sk}}(c)$ 表示密文c的解密。加密和解密算法的细节可以在[38]中找到。它具有以下同态属性：

同态加性： $\forall x,y\in Z_{N},E_{nc}(x)\cdot E_{nc}(y)=E_{nc}(x+ y)$
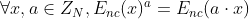
标量乘法： $\forall x,a\in Z_{N},E_{nc}(x)^{a}=E_{nc}(a\cdot x)$

Generalized Paillier 我们的构建还依赖于Damgard-Jurik(DJ)密码系统（Damgard and Jurik [18]引入的），这是一个Paillier加密的泛化形式。消息空间M扩展到 $Z_{N^{^{s}}}$ , $s\geq 1$ , 并且密文空间在 $Z_{N^{^{s+1}}}$ 组之下。如[1]中所述，这种泛化允许人们对消息进行双重加密，并在同一密钥下使用内部加密层的加性同态。具体来说 $\varepsilon ^{2}(x)$ 表示一条消息 $x\in Z_{N^{2}}$ 使用DJ方案的密文, $E_{nc}(x)$ 表示普通的Paillier加密。该扩展允许将第一层的密文视为第二层中的明文。此外，这种嵌套加密在内部密文上保留了结构，并允许人们按如下方式操作它：

我们注意到这是我们的构建所依赖的唯一同态属性。

本文使用~表示加密 $\varepsilon$ 之下的明文是相同的，即 $E_{nc}(x)~E_{nc}(y)\Rightarrow x=y$ .

注意在我们的应用中，我们需要一层加密，也就是说，给定 $\varepsilon ^{2}(E_{nc}(x))$ ,我们想要一个普通Paillier加密 $E_{nc}(x)$ 。如[7]中所介绍的，这可以简单地在S2的帮助下完成。但是，我们需要一个协议RecoverEnc来安全地删除一层加密。

3.4 No-Random-Access (NRA) 算法

NRA算法[22]通过仅利用对关系R的有序访问来找到前k个答案。

输入：有序列表集合S，其中的每一个对象基于不同的属性排列相同的对象集(就是对同一批对象，根据不同的属性排列，按照一个属性排列的结果为一个对象）。

输出：是在聚合输入分数上排序的这些对象的排序列表。

我们选择使用此算法，因为它提供了一种向云服务器泄漏最少信息的方案（因为在查询处理过程中不需要访问中间对象）。我们假设每个列（属性）被独立排序以创建一组排序列表S。排序列表集等同于原始关系，但是每个列表L中的对象根据其本地分数（属性值）按升序排序。排序之后，R包括M个排序列表，表示为S={L1,L2,...,LM}.每个排序列表包括n个数据项，表示为 $L_{i}=\left \{ \left. I_{i}^{1},I_{i}^{2},...,I_{i}^{n} \right \} \right.$ ,每个数据项是一个对象/值对 $I_{i}^{d}=(o_{i}^{d},x_{i}^{d})$ ,其中 $o_{i}^{d}$ 是对象id， $x_{i}^{d}$ 是在第i个分类列表中，深度为d的本地分数（当在每个列表中的分类访问下已经访问了d个对象时）。由于它使用在其精确分数上计算的边界产生前k个答案，因此NRA可能不会报告精确的对象分数。某些对象o的得分下限W（o），是通过对o的已知得分和o未知得分的最小可能值应用排名函数来获得的。 o的得分上界B（o）是通过对o的已知得分和o的未知得分的最大可能值应用排名函数来获得的，这与在相应的排名列表中的最后看到的得分相同。即使其得分未被准确知道，该算法也会报告top-k对象。具体而言，如果对象o的分数下限不低于所有其他对象（包括看不见的对象）的分数上限，则可以安全地将o报告为下一个top-k对象。我们在算法1中给出了NRA的细节。

4.方案概述

本节将给出我们方案的概述。两个给共谋半诚实云服务器表示为S1,S2.

定义4.1 SecTopK = (Enc,Toekn.SecQuery)是包含3个算法Enc,Token,SecQuery的安全top-k查询方案。

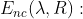$E_{nc}(\lambda ,R):$ 是以关系R和安全参数 $\lambda$ 作为输入，加密关系ER和密钥K作为输出的概率加密算法。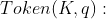
输入是查询点q和密钥K，输出是对于查询点q的token tk.
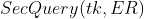：是以tk和ER作为输入的查询处理算法，并基于tk安全的计算top-k结果。

如前所述，我们的加密方案利用了NRA top-k算法。 Enc的思想是加密和置换R的排序列表集，以便服务器可以仅使用对加密数据的顺序访问来执行NRA算法的变体。为了进行这种加密，我们为对象设计了一种新的加密数据结构，称为EHL。Token计算用作陷门的令牌，以便云知道要访问的列表。在SecQuery中，S1按深度扫描每个目标列表的加密数据深度，维护每个深度的加密top-k对象ID列表，直到有k个加密对象id满足NRA暂停条件。在此过程中，S1和S2不了解基础分数和对象。在协议结束时，可以将对象ID报告给客户端。正如我们接下来讨论的那样，之后有两种选择。检索加密记录并将其返回给客户端，或者客户端使用不经意的RAM [24]检索记录，该RAM甚至不显示实际加密记录的位置。在第一种情况下，服务器可以通过观察访问模式（即，不同查询的加密结果）来获得一些附加信息。但是，有一些解决这种访问泄漏的方案[29,32]，超出了本文的范围。第二种方法可能更昂贵但是完全安全。

下面的章节中，我们首先讨论新的加密数据结构EHL和EHL+。然后我们提出三种算法Enc,Token,SecQuery的细节。

5.加密哈希列表(EHL）

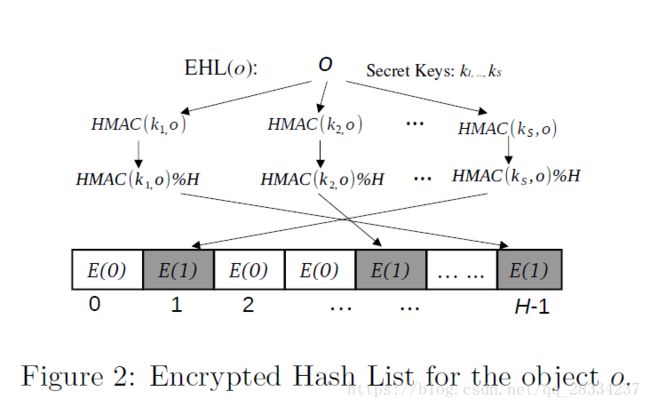
在本文中，我们提出了一种称为加密哈希列表（EHL）的新数据结构来加密每个对象。这种结构的主要目的是允许云同态地计算对象之间的相等性，但是服务器在计算上难以确定对象是什么。直观地，我们的想法是，给定一个对象o，我们使用s个伪随机函数（PRF）将对象散列为长度为H的二进制列表，然后加密列表中的所有位以生成EHL。具体来说，我们使用安全密钥哈希函数HMAC作为PRFs。让EHL(o)成为对象o的加密列表，EHL(o)[i]表示在列表中的第i个加密。具体来说，我们初始化一个长度为H的空列表EHL并且所有项填充为0。首先，生成s个安全密钥k1,k2,..,ks。对象o按照如下规则哈希到一个列表：

1）设置 $EHL[HMAC(ki,o) mod H] = 1 ,for 1\leq i\leq s$

2)使用Paillier加密每一位， $for 0\leq j\leq H-1,E_{nc}(EHL(o)[j]).$ 。

图2展示了我们如何获得一个对象o的EHL(o).

引理5.1 两个对象o1,o2，他们的EHL(o1)和EHL(o2)在计算上是无法区分的。

很明显能看出来阴历5.1成立因为在EHL的每一位都是由Paillier密码系统进行语义安全加密的。给定EHL(x),EHL(y)定义二者之间的随机操作 $\ominus$ 如下：

其中，ri是在Zn中的一些随机值。

引理5.2 让 $E_{nc}(b)=EHL(x)\ominus EHL(y)$ ，若x=y则，明文b = 0(两个对象是相同的),否则b有很高的概率在Zn组上均匀分布。

证明：让 $E_{nc}(x_{i})=EHL(x)[i]$ ， $E_{nc}(y_{i})=EHL(y)[i]$ 。若x=y，即他们是相同的对象，然后对于所有 $i\in [0,H-1],x_{i}=y_{i}$ 。因此，

在 $x\neq y$ 情况下，有高的概率一定是真的，存在 $i\in [0,H-1]$ 使得

即，在EHL（x)中的第I位于EHL(y)不同。假设 $EHL(x)[i]=E_{nc}(1)$ , $EHL(y)[i]=E_{nc}(0)$ 。因此，如下成立：

因此，基于 $\ominus$ 的定义，由此得出b成为在ZN组中均匀分布的随机值。

值得注意的是，人们也可以将BGN密码系统用于上述类似操作，因为BGN方案可以同态地评估二次函数。

False Positive Rate. 请注意，这个构造确实是一个概率加密的Bloom Filter，除了我们为每个对象使用一个列表并加密列表中的每个位。这个EHL的构建可能因为 $\ominus$ 操作产生一些将合法的判断成非法的结果，即在 $x\neq y$ 时， $E_{nc}(0)\leftarrow EHL(x)\ominus EHL(y)$ 。这是因为使用s多个HMAC可以将x和y散列到完全相同的位置。因此，很容易看到false positive rate(FPR)和Bloom Filter一样，在这里可以选择哈希函数HMAC的数量由s变成 $H/n\ln 2$ 来最小化falsepositive rate为

为了降低误报率，我们可以增加列表H的长度。然而，这将增加结构的成本，无论是空间开销还是随机化操作的操作数O（H）。在下一小节中，我们将介绍一种更紧凑，空间效率更高的加密数据结构EHL +

EHL+.现在提出一种计算和空间高效的加密哈希列表EHL+。有效的EHL +的想法是首先将对象o“安全地散列”到更大的空间s次，并且只加密那些哈希值。因此，对于操作 $\ominus$ ，我们只同态的抽取那些哈希值。现在复杂性降低到O（s）而不是O（H），s是使用的安全哈希函数的数量。我们证明，即使使用非常小的s，也可以得到可忽略的误报率。为了创建一个对象o的EHL+(o)，首先生成s个安全密钥k1,...,ks，然后初始化长度为s的EHL+列表。首先计算 $o_{i}\leftarrow HMAC(k_{i},o)modN$ $1\leq i\leq s$ 。这一步把o映射到在一个在组ZN中的元素，即Paillier密码系统的消息空间。然后设置 $EHL+[i]\leftarrow E_{nc}(o_{i})$ $1\leq i\leq s$ .在EHL+(x)和EHL+(y)之间的操作 $\ominus$ 定义与等式1相似。即其中ri是Zn中生成的一些随机值。相似的，EHL+有和EHL相同的属性。 $E_{nc}(b)\leftarrow EHL+(x)\ominus EHL+(y),b=0$ if x=y，否则b有很高的概率在Zn中是随机的。

现在分析EHL+的FPR。当 $x\neq y$ 时， $E_{nc}(0)\leftarrow EHL+(x)\ominus EHL+(y)$ 出现false positive情况。也就是说对于每一个 $i\in [1,s]$ 假设HMAC是伪随机函数，则发生这种情况的概率最多为 $\frac{1}{N^{s}}$ 。取给定的联合约束则FPR最多是注意 $N\approx 2^{\lambda }$ ，因为N是Paillier加密中的两个大素数p和q的乘积，所以是N是大数， $\lambda$ 是安全参数。例如，如果我们将N设置为256位数（Paillier中的128位素数）并设置s = 4或5，那么即使对于数百万条记录，FPR也可以忽略不计。此外，EHL +的大小远小于EHL，因为它只存储s个加密。在下一节中，我们简单地说EHL表示使用EHL +结构的加密哈希列表

Notation。在我们的构造中引入一些notation.让 x=(x1,x2,...xs) $\in Z_{N}^{s}$ ，加密 $E_{nc}(x)$ 表示加密Enc(x1),...,Enc(xs)的串联。此外，我们用 $\odot$ 表示Enc(x)和EHL(y)之间的逐块乘法；也就是说， $c\leftarrow Enc(x)\odot EHL(y)$ ，其中 $ci\leftarrow Enc(xi)\cdot EHL(y)[i]$ $i\in [1,s]$ .

6. 数据库加密

我们在本节中描述数据库加密过程Enc。给定具有M个属性的关系R，数据拥有者首先使用算法2加密该关系。

在ER中每个数据项 $I_{i}^{d}=(o_{i}^{d},x_{i}^{d})$ 在排序列表Li中深度为d被加密为 $E(I_{i}^{d})=\left \langle EHL(o_{i}^{d}),E_{nc_{pk_{p}}}(x_{i}^{d}) \right \rangle$ ,由于所有分数都是在公钥 $pk_{p}$ 下加密的，对于本文的其余部分，我们只需使用Enc（x）来表示公钥 $pk_{p}$ 下的加密Encpkp（x）。除了数据库和M的大小之外，加密的ER不会显示任何内容。在定理6.1中，我们证明这一点通过展示两个加密数据库是无法区分的，如果他们有相同的大小和相同的属性数量。我们用 $\left | R \right |$ 表示关系R的大小。

定理6.1 给定两个关系R1，R2， $\left | R_{1} \right |=\left | R_{2}\right |$ ，并且有相同属性量。算法Enc输出的加密ER1和ER2无法区分。

7. Query Token

考虑类似SQL的查询q = SELECT * FROM ER ORDERED BY $F_{w}(\cdot )$ STOP BY k，其中 $F_{w}(\cdot )$ 是所有属性的加权线性组合。在本文中，为了简化协议的表示，我们考虑二进制权重，因此评分函数只是属性子集的值的总和。但是，请注意非{0,1}权重客户端应该向服务器提供这些权重，服务器可以通过使用Paillier加密的标量乘法属性来简单地调整相同的技术，然后再执行我们接下来讨论的其余协议。在输入密钥K和查询q时，Token（K; q）算法非常简单并且工作如下：客户端指定大小为m的评分属性集M，即 $\left | M \right |=m\leq M$ ，然后从数据拥有者请求密钥K，其中K是对应于伪随机置换P的密钥。然后客户端为每个 $i\in M$ 计算PK（i）并将以下查询令牌发送到云服务器S1：tk=SELECT * FROM ER ORDERED BY STOP BY k。

8. Top-k Query Processing

如上所述，我们的查询处理协议基于NRA算法。然而，技术难点是对加密数据执行算法，而S1不学习任何对象id或数据的任何得分和属性值。我们结合了几种加密协议来实现这一目标。我们的查询处理使用两种最先进的有效和安全协议：[7]引入的EncSort和[11]引入的EncCompare作为构建块。我们跳过这两个协议的详细描述，因为它们不是本文的重点。这里我们只描述它们的功能：1)EncSort: S1有具有加密的键值对 $(E_{nc}(key_{1}),E_{nc}(a_{1}))...(E_{nc}(key_{m}),E_{nc}(a_{m}))$ 和公钥pk的列表，并且S2具有秘密密钥sk。在协议的结尾，S1获得新的加密 $(E_{nc}({key_{1}'}),E_{nc}(a_{1}{}'))...(E_{nc}(key_{m}'),E_{nc}(a_{m}{}'))$ ,其中key/value列表的排序是基于 ${a_{1}}'\leq {a_{2}}'...\leq {a_{m}}'$ 顺序的，并且集合 $\left \{ (key_{1},a_{1}),...,(key_{m},a_{m}) \right \}$ 和 $\left \{ (key_{1}{}',a_{1}{}'),...,(key_{m}{}',a_{m}{}') \right \}$ 是一样的。

2)EncCompare(Enc(a),Enc(b)):S1有公钥pk,两个加密值Enc(a),Enc(b),S2有私钥sk。在协议的最后，S1获得位f，使得 $f:=(a\leq b)$ 。已经针对上述功能提出了几种协议。我们选择[11]中的那个主要是因为它很有效并且完全符合我们的要求。

8.1 Query Processing: SecQuery

我们首先在高级别上给出了对top-k查询处理SecQuery的整体描述。然后在8.2节中，我们详细描述了我们在查询处理中使用的安全子例程：SecWorst，SecBest，SecDedup和SecUpdate。

如前所述，SecQuery使用NRA算法但与原始NRA不同，因为SecQuery无法保持明文中的全局最差/最佳分数。相反，SecQuery必须深度运行安全协议，并根据每个深度的项目同态计算最差/最佳分数。然后，它必须更新到目前为止看到的加密项目的完整列表，其中包含全局最差/最佳分数。最后，服务器S1报告k个加密对象（或对象ID），而不学习任何对象或其分数。

Notations.在加密数据库中我们用 $E(I)=\left \langle EHL(o),Enc(x) \right \rangle$ 表示每一个加密项，其中I是由对象id o和得分x的一项。在查询处理期间，服务器S1需要维持加密项目的当前最佳/最差分数，并且我们用 $E(I)=\left ( EHL(o),Enc(W),Enc(B) \right )$ 表示加密分数项目I，对象id为o，得分为B，最差得分为W.

具体来说，在接收到token tk = SELECT * FROM ER ORDERED BY STOP BY k 后，云服务器S1开始处理该查询。 token tk包含,其通知S1执行对列表的顺序访问。通过维护加密列表T，其包括具有加密的全局最佳和最差分数的项目，S1按深度更新列表T。设 $T^{d}$ 为深度d后的加密列表T的状态。在深度d处，S1首先通过运行SecWorst和SecBest来同态地计算出现在该深度处的每项的局部加密最差/最佳分数。

在SecWorst中，S1输入为当前加密项 $E(I_{i}^{d})=\left \langle EHL(o_{i}^{d}),E_{nc}(x_{i}^{d}) \right \rangle$ 和当前深度在其他列表H中的所有加密项，即 $H=\left \{ E(I_{j}^{d}) \right \}_{j\neq i,j\in M}$ ,S1使用S2运行协议SecWorst，并获得对象 $o_{i}^{d}$ 的加密最差分数。类似的，在协议SecBest中，S1输入是当前加密项 $E(I_{i}^{d})=\left \langle EHL(o_{i}^{d}),E_{nc}(x_{i}^{d}) \right \rangle$ 和列表指针 $\left \{ j \right \}_{j\neq i}$ ，列表指针表示到目前为止看到的所有加密项。S1使用S2运行协议SecBest，并获得对象 $o_{i}^{d}$ 的加密最佳分数。然后S1通过运行带有S2的SecDedup安全地替换具有大的加密最佳分Z的重复加密对象。在SecDeup协议中，S1输入是迄今为止看到的当前加密项 $E(I_{i}^{d})$ ，在执行协议之后，S1得到加密项 $\Gamma _{d}$ ,其中没有重复对象。接下来，S1通过应用SecUpdate将加密的全局列表从状态 $T^{d-1}$ 更新为状态 $T^{d}$ 。之后，S1利用EncSort对不同的加密对象以他们在 $T^{d}$ 中得分进行排序，以获得最初的k个加密对象，这些对象基于迄今为止的最差分数实质上就是前k个对象。如果在某个深度，第（k + 1）个对象的加密最佳分数 $E_{nc}(B_{k+1})$ 小于第k个对象的加密最差分数 $E_{nc}(W_{k})$ ，则协议停止。这可以通过调用协议EncCompare（ $E_{nc}(W_{k})$ , $E_{nc}(B_{k+1})$ ）来检查。接下来是基础NRA算法，很容易看出S1可以正确报告加密的top-k对象。我们在算法3中描述了详细的查询处理。

8.2 Building Blocks

在本节中，我们将介绍SecWorst，SecBest，SecDedup和SecUpdate协议的详细说明。

8.2.1 Secure Worst Score

在每个深度，对于每个加密数据项，服务器S1应该获得加密Enc（W），这是仅基于当前深度项的最差分数。请注意，这与正常的NRA算法不同，因为它计算每个遇到的对象的全局最差可能得分，直到当前深度。我们正式描述了下面的协议设置：

Protocol 8.1. 服务器S1输入 $E(I)=\left \langle EHL(o),Enc(x) \right \rangle$ ，加密项集合H，即 $H=\left \{ E(I_{i}) \right \}_{i=[\left | H \right |]}$ ,where $E(I_{i})=\left \langle EHL(o_{i}),Enc(x_{i}) \right \rangle$ 。公钥 $pk_{p}$ 。服务器S2的输入是 $pk_{p}$ 和 $sk_{p}$ 。SecWorst基于L安全地计算加密的最差排名得分，即S1输出 $E_{nc}(W(o))$ ，其中W（o）是基于列表H的最差得分。

这里的技术挑战是仅基于对象的平等关系来同态地评估加密分数。也就是说，如果对象与L中的另一个o相同，那么我们将得分添加到 $E_{nc}(W(o))$ ，否则，我们不会。但是，我们希望防止服务器知道任何深度的对象之间的关系。我们使用两个服务器S1和S2之间的协议SecWorst(E(I),L)克服了这个问题。我们在算法4中给出了SecWorst的详细协议描述。

直观来说SecWorst的思想是S1首先生成一个随机置换 $\pi$ 并置换在L中项的列表。然后计算在和每个置换 $E(I_{\pi \left ( i \right )})$ 之间的 $E_{nc}(b_{i})$ ,并将 $E_{nc}(b_{i})$ 发送给S2。随机置换防止S2知道o与 $o_{i}$ 其余对象之间的成对关系。然后S2发送 $\varepsilon ^{2}(t_{i})$ 给S1（第13行），基于引理5.2，ti=1如果两个对象是相同的，否则ti=0。S1之后计算 $\varepsilon ^{2}(Enc({x}'_{i}))\leftarrow \varepsilon ^{2}(t_{i})^{Enc(x_{i})}\cdot (\varepsilon ^{2}(1)\varepsilon ^{2}(t_{i})^{-1})^{Enc(0)}$ 。基于DJ加密属性，

因此，若ti=0，则 ${x}'_{i}=0$ ，否则， ${x}'_{i}=x_{i}$ 。S1之后运行 $RecoverEnc(\varepsilon ^{2}(Enc({x}'_{i})),pk_{p},sk_{p})$ (在算法5中描述）来得到 $Enc({x}'_{i})$ ,请注意，协议RecoverEnc也用于其他协议。最后，S1评估以下等式： $Enc(W(o))\leftarrow \prod _{i=1}^{m} Enc({x}'_{i})$ 。 S1可以正确地评估最差得分，因为当ti = 0时，对象oi与o不同，否则，ti = 1.以下公式给出了最差得分的正确计算：

请注意，在协议结束时没有任何内容泄露给S1。然而，在当前深度处向S2显示了一些泄漏功能，我们将在后面的部分中对其进行详细描述。然而，即使通过学习这种模式，S2仍然不知道在这个深度上哪个特定项目与另一个特定项目相同，因为S1在发送到S2之前随机置换项目并且所有内容都已加密。此外，在对象的分数上没有信息泄露。

8.2.2 Secure Best Score

最佳分数的安全计算与计算最差分数不同。下面我们描述S1和S2之间的协议SecBest：

Protocol 8.2 服务器S1输入是 $pk_{p}$ ，在列表Li中的对象o的 $E(I)=\left \langle EHL(o),Enc(x) \right \rangle$ 和一组指向ER中的列表的指针 $P=\left \{ j \right \}_{i\neq j,j\in M}$ 。服务器S2的输入是 $pk_{p}$ , $sk_{p}$ 。协议SecBest安全地计算当前深度d处的加密最佳分数，即，S1最终输出 $E_{nc}(B(o))$ ，其中B（o）是当前深度处的o的最佳分数。

在深度d，让E（I）成为列表Li中的加密项，那么直到该深度的最佳得分是基于该项是否出现在其他列表 $\left \{ L_{j} \right \}_{j\neq i,j\in M}$ 中。 SecBest的详细描述在算法6中描述。

在SecBest中，S1必须扫描其他列表中的加密项目，以安全地评估加密E（I）的当前最佳分数。每个排序列表中最后一次看到的加密项包含最佳可能值（或最低分数）的加密。如果相同的对象o出现在先前的深度中，则将对象的分数同态地添加到加密的最佳分数Enc（B），否则将到目前为止看到的最低分数添加到Enc（B）。具体来说，S1可以同态评估（第九行）：

也就是说如果ti=0意味着项出现在之前的深度中， ${x}'_{i}$ 将会被分配相应的分数 $x_{i}$ ,否则 ${x}'_{i}$ =0。类似的，S1同态的计算如下:如果I这一项没有出现在之前的深度，那么 $(1-\sum _{i}^{d}ti)=1$ ，因为每个ti=0,因此，将会被分配给底值最后，S1同态地将所有加密分数相加并获得加密的最佳分数（第12行）。

8.2.3 Secure Deduplication

在每个深度处，可能会重复计算一些对象，因为相同的对象可能出现在相同深度的不同排序列表中。 S1无法识别重复项，因为项目及其分数是按概率加密的。我们现在提出一个协议，在下面对加密对象进行重复数据删除。

Protocol 8.3 设是一个加密分数项， $E(I)=\left ( EHL(o),Enc(W),Enc(B) \right )$ ，即E(I)与这三项相关联。假设S1的输入是公钥 $pk_{p}$ ，一个加密得分项集合 $Q=\left \{ E(I_{i}) \right \}_{i\in \left \| Q \right \|}$ 。服务器S2输入时公钥 $pk_{p}$ 和私钥 $sk_{p}$ 。在S1和S2之间执行协议SecDedup使S1能够获得加密的不同对象及其分数的新列表，即，在协议结束时，S1输出新的项目列表 $E({I}_{1}'),...,E({I}'_{l})$ ，并且不存在 $i,j\in [l]$ 且 $i\neq j$ ，使得 $o_{i}=o_{j}$ 。此外，新的加密列表不应影响最终的top-k结果。

直观地，在高级别，SecDedup让S2不经意地找到重复的对象及其分数，并将其对象id用一个随机值代替，其分数用一个足够大的值 $Z=N-1\in Z_{N}$ （在消息空间中的最大值）代替。这样，在对最差分数进行排序之后，它将无法出现在前k个列表中。

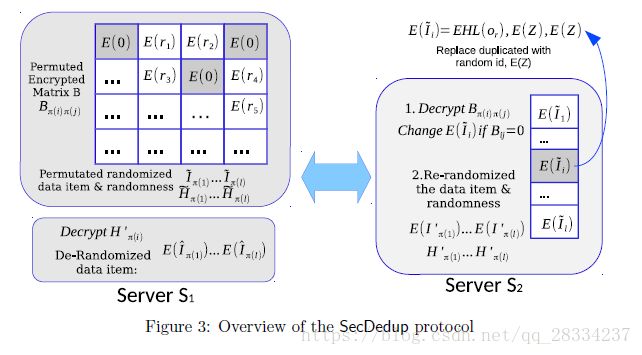
图3给出了我们方法的概况。这里的技术挑战是允许S2找到重复的对象，而不让S1知道哪些对象已被更改。其思想是让服务器S1发送加密的置换矩阵B，其描述列表中对象之间的成对等式关系。 S1然后使用相同的置换来置换盲目加密项目列表，然后将其发送到S2。这可以防止S2知道原始数据。对于重复的对象，S2用足够大的加密最差分数替换分数。另一方面，在重复数据删除之后，S2还必须使数据项blind，以防止S1知道哪些项是重复项。 S1最终获取没有重复的加密项。算法7描述了详细的协议。

我们简要讨论协议的执行情况如下：S1首先通过计算 $EHL(o_{i})\ominus EHL(o_{j})$ 填充条目Bij。注意，由于加密的B是指示列表的相等关系的对称矩阵，因此，S1仅需要填充B的上三角形，并且下三角形可以通过Bij = Bji的事实来填充。另外，S1通过同态地添加随机值来盲目加密项 $Enc(I_{i})$ 并获得 $Enc(\tilde{I_{i}})$ 。这可以防止S2知道项目的值，因为S2具有密钥。此外，S1使用他自己的公钥加密随机数并获得 $H_{i}$ 。为了隐藏列表中对象之间的关系模式，S1把随机置换 $\pi$ 应用到矩阵 $B_{\pi (i)\pi (j))}$ ， $Enc(I_{\pi (i)})$ ， $H_{\pi (i)}$ 中。收到密文之后S2只需要解密矩阵的上三角，若 $b_{\pi (i)\pi (j))}=0$ ，则S2只保留 $Enc(\tilde{I}_{\pi (i)})$ ， $H_{\pi (i)}$ 和 $Enc(\tilde{I}_{\pi (j)})$ ， $H_{\pi (j)}$ 的一个副本。不失一般性的，我们保留 $Enc(\tilde{I}_{\pi (j)})$ , $H_{\pi (j)}$ 并替换 $Enc(\tilde{I}_{\pi (i)})$ ， $H_{\pi (i)}$ 如22-25行。对于没有改变的项，S2也会blind使用他们（28-30行）。值得注意的是，S2添加的随机数是为了防止S1发现哪个项目已被更改。 S2也随机地置换列表（第31行）。S1通过使用他的解密接收的 $H_{\pi (i)}{}'$ 来同态地恢复原始值（参见第35行）。 S1最终是新的加密项目列表。

对于重复的对象，协议用随机值替换它们的对象id，并用一个大数Z替换它的最差分数。对于S2替换的新的加密项（22行） $E(\hat{I_{i}})=\left ( EHL(\hat{o_{i}}),Enc(\hat{W_{i}}),Enc(\hat{B_{i}}) \right )$ ，我们证明 $Enc(\hat{W_{i}})$ 的确是在某些 $j\in [l]$ 上置换 $Enc(W_{{\pi }'(\pi (j))})$ 的新的加密.。真给我们所看到的 $Enc(\hat{W_{i}})$ 被S2的随机 ${\pi }'$ 置换，即 $Enc(W_{{\pi }'(i)})$ (如31行）。因此：

具体地，根据算法7，我们可以看出等式（2）由于第35行而成立，等式（3）因为30，33行成立，等式（4）由于第28行而成立，并且等式（5）成立，因为第10行。另一方面，对于从第22行到第25行S1更改的那些重复项目，通过第35行的S1的同态操作，我们有

由于Z是一个非常大的数字，这个随机生成的对象肯定不会在排序后出现在top-k列表中。

8.2.4 Secure Update

在每个深度d，我们需要使用最新的全局最差/最佳分数更新当前的对象列表。在高级别，S1必须将加密列表 $\Gamma ^{d}$ 从状态 $T^{d-1}$ （先前深度）更新为 $T^{d}$ ，并在此深度处附加新加密项。让 $\Gamma ^{d}$ 成为加密项目列表，他有在深度d处S1得到的加密最差/最佳分数。具体而言，对于深度为d的每个加密项 $E(I_{i})\in T^{d-1}$ 和每个 $E(I_{j})\in L_{d}$ ，我们通过添加来自 $I_{j}$ 的最差来更新 $I_{i}$ 的最差分，并且如果 $I_{i}$ = $I_{j}$ 那么替换他的最佳分数为 $I_{j}$ 的最佳分数。因为 $I_{j}$ 的最差得分是深度最差得分， $I_{j}$ 的最佳得分是最新的最佳得分。如果 $I_{i}\neq I_{j}$ ，那么我们只需将 $E(I_{j})$ 的分数附加到列表中。最后，我们在深度d后获得新的 $T^{d}$ 。我们在算法9中描述了SecUpdate协议。

9. 安全性

由于我们的构造支持比搜索更复杂的查询类型，因此安全性必须捕获对抗性服务器在查询执行期间还从数据和元数据中获取“视图”的事实。我们的top-k查询处理中的CQA安全模型定义了真实世界和理想世界。在现实世界中，对抗服务器和客户端之间的协议就像真正的SecTopK方案一样执行。在理想世界中，我们假设存在两个模拟器Sim1和Sim2，它们从理想的功能中获取泄漏文件，并尝试模拟现实世界的执行。我们说如果在多项式次查询之后，没有ppt区分器只能以不可忽略的概率区分这两个世界，那么该方案是CQA安全的。我们在第9.1节中给出了正式的安全定义。

定义9.1. 设SecTopK=(Enc,Token,SecQuery)是一个top-k查询处理方案并且考虑如下概率实验，其中 $\varepsilon$ 是环境，C是客户端，S1,S2是两个不串通的半城市服务器，Sim1和Sim2是两个模拟器， $L_{Setup},L_{Query}=(L_{Query}^{1},L_{Query}^{2})$ 是（有状态的）泄露函数：

Ideal( $1^{\lambda }$ ):环境 $\varepsilon$ 输出大小为n的关系R，并发送给C。C提交关系R给 $F_{topk}$ ,即一个理想的top-k函数。 $F_{topk}$ 输出 $L_{Setup}(R)$ 和 $1^{\lambda }$ 。并且这两个给Sim1。Sim1产生一个加密ER。

C生成一个多项式数量的自适应选择查询（q1,...,qm)。对于每一个qi，C提交qi给 $F_{topk}$ ，然后 $F_{topk}$ 发送 $L_{Query}^{1}(ER,q_{i})$ 给Sim1， $L_{Query}^{2}(ER,q_{i})$ 给Sim2。

在执行协议之后，C输出 ${OUT}'_{c}$ ,Sim1输出 $OUT_{Sim1}$ ，Sim2输出 $OUT_{Sim2}$

Real( $1^{\lambda }$ ):环境 $\varepsilon$ 输出大小为n的关系R，并发送给C。C计算 $(K,ER)\leftarrow Enc(1^{\lambda },R)$ 并且发送加密的ER给S1.

C生成多项式数量的自适应选择查询（q1; :::; qm）。对于每一个qi，C计算 $tk_{i}\leftarrow Token(K,qi)$ 并把 $tk_{i}$ 发送给S1。S1在S2帮助下运行协议SecQuery(tki，ER）

在协议执行之后，S1发送加密的结果给C。C输出 ${OUT}_{c}$ ，S1输出 $OUT_{S1}$ ,S2输出 $OUT_{S2}$ 。

如果以下内容成立，我们说SecQuery是自适应的（ $(L_{Setup},L_{Query})$ - 语义安全（CQA）：

1. 对于所有 $\varepsilon$ ，对于所有S1，存在一个ppt模拟器Sim1使得以下两个分布集合在计算上无法区分：

2.对于所有 $\varepsilon$ ，对于所有S2，存在一个ppt模拟器Sim2使得以下两个分布集合在计算上无法区分：

我们正式定义在SecTopK中的泄露函数。设setup leakage $L_{Setup}=(\left | R \right |,|M|)$ 即数据库大小和属性的总量。 $L_{Setup}$ 是执行完Enc，向S1泄露的文件。在查询处理期间，我们允许 $L_{Query}=(L_{Query}^{1},L_{Query}^{2})$ 泄露给服务器。注意 $L_{Query}^{1}$ 是S1的泄露函数， $L_{Query}^{2}$ 是S2的泄露函数。在我们的方案中， $L_{Query}^{1}=(QP,D_{q})$ ，QP是查询模式表示是否一个查询已经重复过了。形式上，对于 $q_{j}\in \textbf{q}$ ，查询模式QP(qj）是一个长度为j的二进制向量，若qj=qi则在位置i处值为1否则为0。 $D_{q}$ 是查询q的暂停深度。对于任何查询q，我们定义相等模式如下：假设每个深度有m个对象，那么

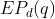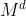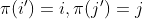Equality Pattern $EP_{d}(q)$ :一个对称的二进制m*m矩阵 $M^{d}$ ,若存在 $o_{\pi ({i}')}=o_{\pi ({j}')}$ 则 $M^{d}[i,j]=1$ ，对于一些随机置换 $\pi$ 来说， $\pi ({i}')=i,\pi ({j}')=j$ .否则 $M^{d}[i,j]=0$ .

然后设 $L_{Query}^{2}=(\left \{ EP_{d}(q) \right \}_{i=1}^{D_{q}})$ ，即在深度 $d\leq D_{q}$ 相等模式表示在对象之间相等的数量。注意， $EP^{d}(q)$ 不泄漏原始数据库中任何深度处的对象之间的相等关系，即服务器从不知道哪些对象是相同的，因为服务器不知道置换。

定理9.2. 假设EHL中使用的函数是伪随机函数而Paillier加密是CPA安全的，那么我们提出的方案SecTopK =（Enc; Token; SecQuery）是 $(L_{Setup},L_{Query})$ -CQA安全。

证明：略。

10 查询优化

在本节中，我们将介绍一些可以提高协议性能的优化。优化是双重的：1）我们以牺牲一些额外的隐私泄漏为代价来优化协议SecDedup的效率，以及2）我们建议批量处理SecDupElim和EncSort以进一步改进SecQuery。

10.1 Efficient SecDupElim

我们现在介绍提供与SecDedup类似功能的高效协议SecDupElim。回想一下，在每个深度，S1运行SecDedup以重复删除m个加密对象，然后在执行SecDedup后，S1仍然接收m个项目但没有重复，并在运行SecUpdate时将这些m个对象添加到列表 $T^{d}$ 。因此，当我们执行昂贵的排序算法EncSort时，要排序的列表大小在深度d处具有md元素。

SecDupElim的想法是，SecDupElim不再保留相同数量的加密项m，而是消除了重复的对象。这样，加密对象的数量就会减少，尤其是在有许多重复对象的情况下。可以通过简单地更改SecDedup来获得SecDupElim，如下所示：在第20行的算法7中，当S2观察到存在重复的对象时，S2仅保留它们的一个副本。该算法与之前的算法完全相同，但没有执行第22-25行。我们还在SecUpdate的第13行运行SecDupElim而不是SecDedup。也就是说，在安全更新之后，我们只保留具有更新分数的不同对象。因此，要排序的项数也减少。现在通过调整SecDupElim，如果列表中出现了许多重复的对象，我们需要更少的加密项进行排序。

Remark on security.SecDupElim会向服务器S1泄漏其他信息。 S1在深度d处学习唯一性模式(uniqueness pattern $UP^{d}(q_{i})$ ，其中 $UP^{d}(q_{i})$ 表示出现在当前深度d的唯一对象的数量。深度d处的不同加密值独立于所有其他深度，因此，该协议仍然保护原始ER的分布。另外，由于在协议执行期间的“重新加密”，所有加密都是新的加密，即，与ER的加密不同。最后，我们强调，由于它们都是加密的，因此没有发现对象及其值的任何内容。

10.2 Batch Processing for SecQuery

在查询处理SecQuery中，我们发现我们不需要为每个深度运行SecDupElim和EncSort协议。由于SecDupElim和EncSort是SecQuery中成本最高的协议，因此我们可以执行批处理并在几个深度之后执行它们，而不是在每个深度执行它们。我们的观察是没有必要在每个扫描深度重复删除重复的对象。如果我们在某些扫描深度之后执行SecDupElim，则将消除重复的对象，并且将通过运行EncSort对具有更新的最差和最佳分数的那些不同的加密对象进行排序。该协议将保持正确。我们引入一个参数p使得 $p\geq k$ 。参数p指定我们需要在SecQuery协议中哪里运行SecDupElim和EncSort。也就是说，服务器S1和S2运行SecQuery与算法3相同，除了每个p深度我们在算法3中运行第9-12行以检查算法是否可以停止。此外，我们可以在批处理中使用原始SecDedup替换SecDupElim，以获得更好的隐私，但要牺牲效率。

Security. 与SecDupElim的优化相比，我们证明了批处理策略提供的隐私比仅运行SecDupElim更多。对于查询q，假设我们计算m个属性的分数。回想一下，在运行SecDupElim时，深度为p的 $UP^{d}(q)$ 已经泄露给S1，因此，在第一个深度之后，在最坏的情况下，S1得知第一个深度处的物体是同一个物体。为了防止这种最坏情况的泄漏，我们每隔p深度执行一次SecDupElim。然后S1学习在最坏的情况下有p个不同的对象。在深度p之后，S1可以在表格中正确定位那些不同的加密对象位置的概率最多为 $\frac{1}{(p!)^{m}}$ 。对于较大的p，这会快速下降。然而，在实践中，这种泄漏非常小，因为每p深度出现许多不同的对象。与我们的所有协议类似，由于服务器的“重新加密”，所以加密是新的。即使S1有可能猜测不同对象的位置，但由于它们都是加密的，因此对象ID及其分数尚未显示。

10.3 Efficiency

我们分析查询执行的效率。假设客户端为查询选择m个属性，因此在每个深度都有m个对象。在深度d，执行SecWorst需要S1花费时间，执行SecBest需要，SecDedup需要 $O(m^{2})$ ，SecUpdate需要 $O(m^{2}d)$ 。 S2的复杂性是相似的。另外，EncSort有时间开销 $O(m\log ^{2}m)$ ; 但是，我们可以通过调整并行性进一步降低到 $O(\log ^{2}m)$ （见[7]）。另一方面，SecDupElim只占用 $O(u^{2})$ ，其中u是此深度处不同对象的数量。请注意，大多数计算都是乘法（同态加法），因此查询处理的成本相对较小。

11 Experiments

12 Top-k Join

我们想简要提一下，我们的技术还可以扩展到计算多个加密关系的top-k连接查询。给定一组关系，R1; :::; RL，Ri中的每个元组都与某个得分相关联，这使得它在Ri中排名。前k个连接查询将R1连接到RL，并生成按总分排名的结果。根据某个功能F计算总得分，该功能组合了各个得分。我们在本文中仅考虑（即.equi-join）条件。类似地，我们在本文中考虑的得分函数F也是来自加入关系的属性的线性组合。可能的类似SQL的连接查询示例如下：Q1 = SELECT * FROM A，B，C WHERE A.1 = B.1和B.2 = C.3 ORDER BY A.1 + B.2 + C. 4停止后k;其中A，B和C是三个关系，A.1，B.1，B.2，C.3，C.4是这些关系的属性。我们的想法是设计一个安全的连接运算符，表示为./sec，这样服务器S1就会根据收到的令牌不经意地加入关系。 S1必须使用S2调用协议以获得满足连接条件的结果连接结果。

你可能感兴趣的:(Top-k Query Processing on Encrypted Databases with Strong Security Guarantees)

深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
Mongodb Error: queryTxt ETIMEOUT xxxx.wwwdz.mongodb.net 佛一脚 error react mongodb 数据库
背景每天都能遇到奇怪的问题，做个记录，以便有缘人能得到帮助！换了一台电脑开发nextjs程序。需要连接mongodb数据，对数据进行增删改查。上一台电脑好好的程序，新电脑死活连不上mongodb数据库。同一套代码，没任何修改，搞得我怀疑人生了，打开浏览器进入mongodb官网毫无问题，也能进入线上系统查看数据，网络应该是没问题。于是我尝试了一下手机热点，这次代码能正常跑起来，连接数据库了！！！是不
vue+el-table 可输入表格使用上下键进行input框切换以对_ vue学习记录 vue.js javascript 前端
使用上下键进行完工数量这一列的切换-->//键盘触发事件show(ev,index){letnewIndex;letinputAll=document.querySelectorAll('.table_inputinput');//向上=38if(ev.keyCode==38){if(index==0){//如果是第一行,回到最后一个newIndex=inputAll.length-1}elsei
00. 这里整理了最全的爬虫框架（Java + Python）有一只柴犬爬虫系列爬虫 java python
目录1、前言2、什么是网络爬虫3、常见的爬虫框架3.1、java框架3.1.1、WebMagic3.1.2、Jsoup3.1.3、HttpClient3.1.4、Crawler4j3.1.5、HtmlUnit3.1.6、Selenium3.2、Python框架3.2.1、Scrapy3.2.2、BeautifulSoup+Requests3.2.3、Selenium3.2.4、PyQuery3.2
python获取子进程返回值_Python对进程Multiprocessing子进程返回值 weixin_39752157 python获取子进程返回值
在实际使用多进程的时候，可能需要获取到子进程运行的返回值。如果只是用来存储，则可以将返回值保存到一个数据结构中；如果需要判断此返回值，从而决定是否继续执行所有子进程，则会相对比较复杂。另外在Multiprocessing中，可以利用Process与Pool创建子进程，这两种用法在获取子进程返回值上的写法上也不相同。这篇中，我们直接上代码，分析多进程中获取子进程返回值的不同用法，以及优缺点。初级用法
spring security中几大组件的作用和执行顺序阿信在这里 java spring
springsecurity中几大组件的作用和执行顺序在SpringSecurity中，AuthenticationProvider、GroupPermissionEvaluator、PermissionEvaluator、AbstractAuthenticationProcessingFilter、DefaultMethodSecurityExpressionHandler和ManageSecu
Vue + Express实现一个表单提交九旬大爷的梦
最近在折腾一个cms系统，用的vue+express，但是就一个表单提交就弄了好久，记录一下。环境：Node10+前端：Vue服务端：Express依赖包：vueexpressaxiosexpress-formidableelement-ui（可选）前言：axiosget请求参数是：paramsaxiospost请求参数是：dataexpressget接受参数是req.queryexpresspo
ElasticSearch查询超过10000条（1000页）时出现Result window is too large的问题王月亮17
问题当ES数据量较大，使用分页查询超过10000条（1000页）时，出现如下错误：Cannotexecutejestaction,responsecode:500,error:{"root_cause":[{"type":"query_phase_execution_exception","reason":"Resultwindowistoolarge,from+sizemustbelesstha
Scanpy源码浅析之pp.normalize_total 何物昂
版本导入Scanpy,其版本为'1.9.1'，如果你看到的源码和下文有差异，其可能是由于版本差异。importscanpyasscsc.__version__#'1.9.1'例子函数pp.normalize_total用于Normalizecountspercell，其源代码在scanpy/preprocessing/_normalization.py我们通过一个简单例子来了解该函数主要功能:将一
MySQl篇（SQL - 基本介绍）（持续更新迭代） wclass-zhengge mysql sql 数据库
目录一、简介二、SQL方言（分页查询为例）1.简介2.SQL方言大比拼2.1.Oracle2.1.1.使用ROWNUM实现分页查询2.1.2.使用ROW_NUMBER()实现分页查询2.2.MySQL2.3.PostgreSQL三、语法规范四、注释五、MySQL脚本中的标点符号一、简介1、SQL是结构化查询语言（StructureQueryLanguage），专门用来操作/访问关系型数据库的通用语
C# 开发教程-入门基础天马3798 教程系列整理 c#开发语言
1.C#简介、环境，程序结构2.C#基本语法，变量，控制局域，数据类型，类型转换3.C#数组、循环，Linq4.C#类，封装，方法5.C#枚举、字符串6.C#面相对象，继承，封装，多态7.C#特性、属性、反射、索引器8.C#委托，事件，集合，泛型9.C#匿名方法10.C#多线程更多：JQuery开发教程入门基础Vue开发基础入门教程Vue开发高级学习教程
Sentinel实时监控不展示问题朱杰jjj sentinel sentinel
问题官方插件Endpoint支持，可以实时统计出SpringBoot的健康状况和请求的调用信息在使用Endpoint特性之前需要在Maven中添加spring-boot-starter-actuator依赖，并在配置中允许Endpoints的访问。SpringBoot1.x中添加配置management.security.enabled=false。暴露的endpoint路径为/sentinelS
基于Python执行lua脚本 xu-jssy Python自动化脚本 python lua 自动化 rpa
一、依赖安装pipinstalllupa二、源码将lua文件存放在base_path路径，将lua文件名称（不包含后缀名）传递给lua_runner函数即可importmultiprocessingimportlupa#lua文件存放位置base_path='D:\\test\\lua'classLuaFuncion:#创建Lua运行时环境lua=lupa.LuaRuntime(unpack_re
【Python爬虫】百度百科词条内容 PokiFighting 数据处理 python 爬虫开发语言
词条内容我这里随便选取了一个链接，用的是FBI的词条importurllib.requestimporturllib.parsefromlxmlimportetreedefquery(url):headers={'user-agent':'Mozilla/5.0(WindowsNT6.1;Win64;x64)AppleWebKit/537.36(KHTML,likeGecko)Chrome/80.
Jooq 框架介绍及其核心要点木南曌 Java java
一、引言Jooq（JavaPersistenceforRelationalDatabases）是一个强大的类型安全的SQL查询构建器和ORM（Object-RelationalMapping）框架，专为Java和Kotlin设计。它为开发者提供了一种优雅的方式来编写SQL代码，同时还能享受到静态类型检查带来的好处。本文将详细介绍Jooq的核心功能，并通过一系列的代码示例来展示如何使用Jooq。二、
Spring Security静态资源过滤（11）小黑屋说YYDS spring
在一个实际项目中，并非所有的请求都需要经过SpringSecurity过滤器，有一些特殊的请求，例如静态资源等，一般来说并不需要经过SpringSecurity过滤器链，用户如果访问这些静态资源，直接返回对应的资源即可。回顾关于WebSecurity的讲解，提到它里边维护了一个ignoredRequests变量,该变量，记录的就是所有需要被忽略的请求，这些被忽略的请求将不再经过SpringSecu
Spring Security定义多个过滤器链（10）小黑屋说YYDS spring
在SpringSecurity中可以同时存在多个过滤器链，一个WebSecurityConfigurerAdapter的实例就可以配置一条过滤器链。我们来看如下一个案例：@ConfigurationpublicclassSecurityConfig{@BeanUserDetailsServiceus(){InMemoryUserDetailsManagerusers=newInMemoryUser
SpringSecurity初学总结 weixin_66442229 spring
springSecurity安全框架基于Java的安全框架主要有:SpringSecurity和Shiro介绍基础概念安全框架是对用户访问权限的控制,保证应用的安全性。其主要的工作是用户认证和用户授权|鉴权主要应用于Spring的企业应用系统,提供声明式的安全访问控制解决方案。它提供了一组可以在Spring应用上下文中配置的Bean能很好的结合Spring的DI依赖注入和AOP面向切面编程功能应用
MySQL 源码｜55 - 语法解析(V2)：基础查询语句（query_specification）｜V20240915 长行 MySQL源码 mysql 源码语法解析查询
目录文档：MySQL源码｜源码剖析文档目录源码位置（版本=MySQL8.0.37）：sql/sql_yacc.yy前置文档：MySQL源码｜68-语法解析(V2)：LOCKING子句（锁定读取）｜V20240909MySQL源码｜39-语法解析(V2)：ORDERBY子句｜V20240814｜V20240912（第2版）MySQL源码｜40-语法解析(V2)：GROUPBY子句｜V20240814
springcloud — 微服务鉴权管理Spring Security原理解析(二) RachelHwang springcloud spring java spring security oauth2 springcloud
引言：回顾之前介绍的OAuth2简单分析与介绍，微服务鉴权管理之OAuth2原理解析(一)，前面的部分，我们关注了SpringSecurity是如何完成认证工作的，但是另外一部分核心的内容：过滤器，一直没有提到，我们已经知道SpringSecurity使用了springSecurityFilterChain作为了安全过滤的入口，这一节主要分析一下这个过滤器链都包含了哪些关键的过滤器，并且各自的使命
Apache Shiro安全框架(2)-用户认证 heyrian Java shiro
身份认证在shiro中用户需要提供用户的principals（身份）和credentials（证明）来证明该用户属于当前系统用户。常见的认证方式即用户名/密码。在解释身份认证之前，我们先来看看shiro中的Subject和Realm,这是身份认证的两个关键的概念。Subjectsubject代表当前用户，内部主要维护当前用户信息。shiro中所有的subject都交给SecurityManager
解决mysql漏洞 Oracle MySQL Server远程安全漏洞(CVE-2015-0411) dieweidong5625 数据库运维 java
有时候会检测到服务器有很多漏洞，而大部分漏洞都是由于服务的版本过低的原因，因为官网出现漏洞就会发布新版本来修复这个漏洞，所以一般情况下，我们只需要对相应的软件包进行升级到安全版本即可。通过查阅官网信息，OracleMySQLServer远程安全漏洞(CVE-2015-0411)，受影响系统：OracleMySQLServer/usr/databases.sql//先备份原有所有数据，防止数据丢失。
Spring Cloud: Hystrix请求队列线程不足 MeazZa
在SpringCloud中，Feign可以实现本地化的微服务API调用，Hystrix可以实现调用失败时的fallback处理。问题描述：在实际生产环境中使用时，我们遇到了这样一个错误："...,stacktrace:[com.netflix.hystrix.exception.HystrixRuntimeException:QueryNodeImpalaBdService#getQueryRes
Servlet容器的作用、HttpServlet的工作机制流程图烟雨国度 servlet 流程图 hive
HttpServletRequest解析过程是否GETPOST其他方法Servlet生命周期init-初始化Servletservice-处理请求destroy-销毁ServletgetMethod返回HTTP方法getRequestURI返回请求URIgetQueryString返回查询字符串getParameter返回特定参数值客户端发送HTTP请求服务器接收请求Web容器创建ServletR
MySQL内存结构 san.hang 数据库数据结构与算法
实际上MySQL内存的组成和Oracle类似，也可以分为SGA（系统全局区）和PGA（程序缓存区）。mysql>showvariableslike"%buffer%";一、SGA1.innodb_buffer_bool用来缓存Innodb表的数据、索引、插入缓冲、数据字典等信息。2.innodb_log_buffer事务在内存中的缓冲，即redlogbuffer的大小3.querycache高速查
html 删除事件,html 事件的添加和删除列蒂齐亚 html 删除事件
jQuery在jQuery1.7版本中bind()unbind(),live()die(),on()off(),delegate()下面我们给li元素添加事件bind()旧版写法:事件不能适用脚本创建的新元素live()旧版写法:适用脚本创建的新元素写法，但性能极不好on()新版写法，事件不能适用脚本创建的新元素(接收多个函数绑定)这三种方法都是基于要给添加事件的元素本身。$("ulli").bi
动态生成的html元素绑定click事件 .NET跨平台 Jquery及其组件 html jquery
第一篇博客，开启技术博客的生涯，欢迎大家批评指教（坚信妹子也可以做好程序猿）今天想说帮公司做项目的时候遇到的一个小问题，动态添加html元素以后再去事件监听出问题。在实际开发中会遇到要给动态生成的html元素绑定触发事件的情况。就是上面的一张表格要动态实现添加行，然后序列号还要随着增加，当删除的时候序列号依旧是按顺序排列。刚开始使用jQuery的on方法来解决，但是发现一个问题会出现事件绑定很多次
详解 Pandas 的 query 函数文刀小桂 Pandas pandas python 开发语言
Pandas的query()方法能够使用字符串表达式来筛选DataFrame数据的行，类似于SQL的where子句importpandasaspddf=pd.DataFrame({"A":[1,3,5,6,7],"B":[11,10,9,8,12],"C":["hello","pandas","python","java","shell"],"D":["2024-02-01","2023-12-1
prometheus中step或resolution的含义 iceman1952 prometheus
prometheus官方文档对resolution的解释真是语焉不详，只有下面寥寥几句话Queryingexamples|PrometheusSubqueryReturnthe5-minuterateofthehttp_requests_totalmetricforthepast30minutes,witharesolutionof1minute.rate(http_requests_total[
前端页面实现table可拖动改变列宽牧码人 js jQuery js 表格拖动 css colResizable
此处实现页面的table表格可以自由拖动列宽，拖动时表格内文字不换行，超出部分以...代替，实现步骤如下：1.首先引入jQuery和colResizable的js文件，colResizable支持表格拖动改变列宽，但基于jQuery，（1）colResizable可以去：http://www.bacubacu.com/colresizable/#rangeSlider下载（2）引入文件：2.编写j
LeetCode[Math] - #66 Plus One Cwind java LeetCode 题解 Algorithm Math
原题链接：#66 Plus One 要求：给定一个用数字数组表示的非负整数，如num1 = {1, 2, 3, 9}, num2 = {9, 9}等，给这个数加上1。注意： 1. 数字的较高位存在数组的头上，即num1表示数字1239 2. 每一位（数组中的每个元素）的取值范围为0~9 难度：简单分析：题目比较简单，只须从数组
JQuery中$.ajax()方法参数详解 AILIKES JavaScript jsonp jquery Ajax json
url: 要求为String类型的参数，（默认为当前页地址）发送请求的地址。 type: 要求为String类型的参数，请求方式（post或get）默认为get。注意其他http请求方法，例如put和 delete也可以使用，但仅部分浏览器支持。 timeout: 要求为Number类型的参数，设置请求超时时间（毫秒）。此设置将覆盖$.ajaxSetup()方法的全局
JConsole & JVisualVM远程监视Webphere服务器JVM Kai_Ge JVisualVM JConsole Webphere
JConsole是JDK里自带的一个工具，可以监测Java程序运行时所有对象的申请、释放等动作，将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。　　使用JConsole工具来分析WAS的JVM问题，需要进行相关的配置。　　首先我们看WAS服务器端的配置. 　　1、登录was控制台https://10.4.119.18
自定义annotation 120153216 annotation
Java annotation 自定义注释@interface的用法一、什么是注释说起注释，得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说，元数据是描述数据的。就象数据表中的字段一样，每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据，也就是说注释是描述java源
CentOS 5/6.X 使用 EPEL YUM源 2002wmj centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
在SQLSERVER中查找缺失和无用的索引SQL 357029540 SQL Server
--缺失的索引 SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement , last_user_seek ,
Spring3 MVC 笔记（二） —json+rest优化 7454103 Spring3 MVC
接上次的 spring mvc 注解的一些详细信息！其实也是一些个人的学习笔记呵呵！
替换“\”的时候报错Unexpected internal error near index 1 \ ^ adminjun java “\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘... 在拆分字符串时遇到通过 \ 来拆分，可是用所以想通过转义 \\ 来拆分的时候会报异常 public class Main { /*
POJ 1035 Spell checker(哈希表) aijuans 暴力求解--哈希表
/* 题意：输入字典，然后输入单词，判断字典中是否出现过该单词，或者是否进行删除、添加、替换操作，如果是，则输出对应的字典中的单词要求按照输入时候的排名输出题解：建立两个哈希表。一个存储字典和输入字典中单词的排名，一个进行最后输出的判重 */ #include <iostream> //#define using namespace std; const int HASH =
通过原型实现javascript Array的去重、最大值和最小值 ayaoxinchao JavaScript array prototype
用原型函数（prototype）可以定义一些很方便的自定义函数，实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。实现代码如下： <script type="text/javascript"> Array.prototype.unique = function() { var a = {}; var le
UIWebView实现https双向认证请求 bewithme UIWebView https Objective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求中有讲述，不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求，网上有些文章中有涉及到此内容，但都只言片语，没有讲完全，更没有完整的代码，让人困扰不已。但是此知
NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存) bijian1013 redis 数据库 NoSQL
3.事务处理 Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行，而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时，这个连接会进入一个事务上下文，该连接后续的命令不会立即执行，而是先放到一个队列中，当执行exec命令时，redis会顺序的执行队列中
各数据库分页sql备忘 bingyingao oracle sql 分页
ORACLE 下面这个效率很低 SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20; 下面这个效率很高 SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
【Scala七】Scala核心一：函数 bit1129 scala
1. 如果函数体只有一行代码，则可以不用写{},比如 def print(x: Int) = println(x) 一行上的多条语句用分号隔开，则只有第一句属于方法体，例如 def printWithValue(x: Int) : String= println(x); "ABC" 上面的代码报错，因为，printWithValue的方法
了解GHC的factorial编译过程 bookjovi haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的，一部分原因是haskell本身的设计就不易于实现compiler，如lazy特性，static typed，类型推导等。关于GHC的内部实现有篇文章说的挺好，这里，文中在RTS一节中详细说了haskell的concurrent实现，里面提到了green thread，如果熟悉Go语言的话就会发现，ghc的concurrent实现和Go有点类
Java-Collections Framework学习与总结-LinkedHashMap BrokenDreams LinkedHashMap
前面总结了java.util.HashMap，了解了其内部由散列表实现，每个桶内是一个单向链表。那有没有双向链表的实现呢？双向链表的实现会具备什么特性呢？来看一下HashMap的一个子类——java.util.LinkedHashMap。
读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory bylijinnan abstract
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * Abstract Factory Pattern * 抽象工厂模式的目的是： * 通过在抽象工厂里面定义一组产品接口，方便地切换“产品簇” * 这些接口是相关或者相依赖的
压暗面部高光 cherishLC PS
方法一、压暗高光&重新着色当皮肤很油又使用闪光灯时，很容易在面部形成高光区域。下面讲一下我今天处理高光区域的心得：皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道（Lab模式的L通道）决定，色彩则由a、b通道确定。处理思路为在保持高光区域纹理的情况下，对高光区域着色。具体步骤为：降低高光区域的整体的亮度，再进行着色。如果想简化步骤，可以只进行着色（参看下面的步骤1
Java VisualVM监控远程JVM crabdave visualvm
Java VisualVM监控远程JVM JDK1.6开始自带的VisualVM就是不错的监控工具. 这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面通过JMX连接远程机器, 需要经过下面的配置: 1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
Saiku去掉登录模块 daizj saiku 登录 olap BI
1、修改applicationContext-saiku-webapp.xml <security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" /> <security:intercept-url pattern=&qu
浅析 Flex中的Focus dsjt html Flex Flash
关键字：focus、 setFocus、 IFocusManager、KeyboardEvent 焦点、设置焦点、获得焦点、键盘事件一、无焦点的困扰——组件监听不到键盘事件原因：只有获得焦点的组件（确切说是InteractiveObject）才能监听到键盘事件的目标阶段；键盘事件（flash.events.KeyboardEvent）参与冒泡阶段，所以焦点组件的父项（以及它爸
Yii全局函数使用 dcj3sjt126com yii
由于YII致力于完美的整合第三方库，它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如，Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数，使得代码看起来更加简洁易用。(原文地址) 我们可以保存在globals.php在protected目录下。然后，在入口脚本index.php的，我们包括在
设计模式之单例模式二（解决无序写入的问题） come_for_dream 单例模式 volatile 乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题，但是因为由于JVM为了使得处理器内部的运算单元能充分利用，处理器可能会对输入代码进行乱序执行（Out Of Order Execute）优化，处理器会在计算之后将乱序执行的结果进行重组，保证该
程序员从初级到高级的蜕变 gcq511120594 框架工作 PHP android html5
软件开发是一个奇怪的行业，市场远远供不应求。这是一个已经存在多年的问题，而且随着时间的流逝，愈演愈烈。我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题，当然这些方法常常不管用，于是，唯一能做的就是不断地尝试，逐个看看是否奏效”。现在我们把淫浸代码时间超过3年的开发人员称为
Reverse Linked List hcx2013 list
Reverse a singly linked list. /** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ p
Spring4.1新特性——数据库集成测试 jinnianshilongnian spring 4.1
目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
C# Ajax上传图片同时生成微缩图(附Demo) liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。（jquery + c# ashx） 2.C#位图处理 System.Drawing。 3.最新demo支持IE7,IE8,Fir
Java list三种遍历方法性能比较 pda158 java
从c/c++语言转向java开发，学习java语言list遍历的三种方法，顺便测试各种遍历方法的性能，测试方法为在ArrayList中插入1千万条记录，然后遍历ArrayList，发现了一个奇怪的现象，测试代码例如以下： package com.hisense.tiger.list; import java.util.ArrayList; import java.util.Iterator;
300个涵盖IT各方面的免费资源（上）——商业与市场篇 shoothao seo 商业与市场 IT资源免费资源
A.网站模板+logo+服务器主机+发票生成 HTML5 UP:响应式的HTML5和CSS3网站模板。 Bootswatch:免费的Bootstrap主题。 Templated:收集了845个免费的CSS和HTML5网站模板。 Wordpress.org|Wordpress.com:可免费创建你的新网站。 Strikingly:关注领域中免费无限的移动优
localStorage、sessionStorage uule localStorage
W3School 例子 HTML5 提供了两种在客户端存储数据的新方法： localStorage - 没有时间限制的数据存储 sessionStorage - 针对一个 session 的数据存储之前，这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储，因为它们由每个对服务器的请求来传递，这使得 cookie 速度很慢而且效率也不