Pytorch入门之线性回归

这里定义一个简单的神经网络来做一个线性回归问题

神经元之间的线就不连了，大家知道是个全连接层就好

 

1、网络类的编写及生成网络

搭建这样一个网络，首先就是需要定义一个class，class必须得继承nn.Module类，常用来被继承，然后用户去编写自己的网络/层。

类中的初始化部分需要去例化自己的层。这里需要定义2个全连接层，因此我们可以直接调用nn.Linear这个类，关于这个类不清楚的，可以看看我的另一篇文章：https://blog.csdn.net/MR_kdcon/article/details/108918272

self.hidden_layers = nn.Linear(feature_in, feature_hidden)
self.predict_layers = nn.Linear(feature_hidden, feature_out)

类中的前向传播函数需要去模拟前向传播的过程，即输入经过全连接层然后通过激励函数输出，接着又通过输出端的全连接层继续输出成最终的预测值

out0 = self.hidden_layers(datain).relu()
out1 = self.predict_layers(out0)

这样一来，我们的网络就编写好了。

接下来，就是去生成这个网络，就是例化这个类。接着定义一个有序容器Squential，将上面这个网络依次装进去

net = Net(1, 1, 10)
network = nn.Sequential()
network.add_module('full0', net.hidden_layers)
network.add_module('dull1', net.predict_layers)

我们可以打印一下这个网络

很清晰的显示了这2个全连接层。

 

 

2、参数初始化

网络生成好了，接下来就是对网络参数进行初始化

我们导入torch.nn中的init模块

# 初始化参数w b
init.normal_(network[0].weight, 0, 0.01)  # 服从均值0，方差0.01的正太分布
init.normal_(network[1].weight, 0, 0.02)  # 服从均值0，方差0.01的正太分布
init.constant_(network[0].bias, 0)  # 填充函数
init.constant_(network[1].bias, 0)  # 填充函数

我们可以打印一下这个参数看看，net.parameters()，用来查看网络net中的参数，全连接层中的参数就是(w, b)

for param in network.parameters():
    print(param)

 

 

 

3、前向推理，反向传播，训练前的准备工作

1、定义损失函数，这里我们就选均方误差

loss = nn.MSELoss()

2、生成优化器 ，这里我们选用SGD

optimizer = optim.SGD(network.parameters(), lr=0.2)  #例化对象

有关SGD的详细介绍在我的另一篇文章中，有兴趣的可以看看：https://blog.csdn.net/MR_kdcon/article/details/108922056

 

 

 

4、前向、后向、训练

在提前定义好的epochs下，进行前向传播，计算Loss，然后清空梯度，反向传播计算梯度，SGD优化损失函数。写成代码就是：

for epoch in range(epochs):
    out_forward = network(y)
    target_func = loss(out_forward, y)
    optimizer.zero_grad()  # 或者network.zero_grad()
    target_func.backward()
    optimizer.step()

这一样一来，整个网络就训练好了

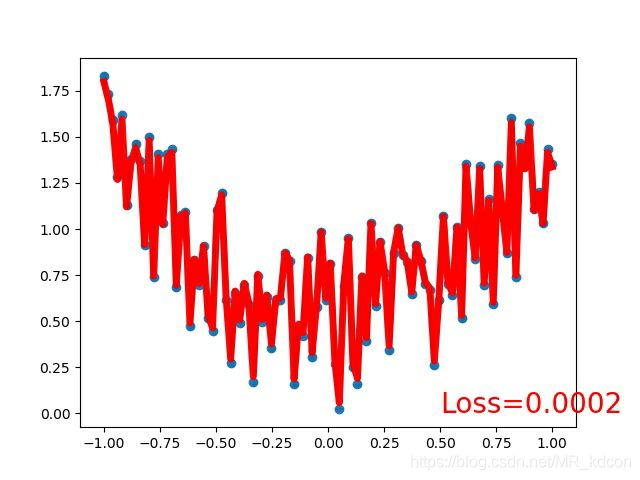
这是最后在训练集上拟合的情况：

 

总结一下，整个学习任务的四步骤：

1、网络类的编写及生成网络

2、初始化模型参数

3、训练前的准备，即定义损失函数、生成优化器

4、前向推理、反向传播、训练