加权最小均方误差算法（WMMSE）论文复现，附Matlab代码

引言

加权最小均方误差算法（Weighted Minimum Mean-Square Error， WMMSE）是多用户无线通信网络优化中最常用到的算法，但该算法实现较为复杂。网上看到的完整复现的代码较少，因此，本文复现Q Shi et al的经典论文《An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel》，该论文到目前引用量高达1400多次，说明了WMMSE算法在无线通信中的影响力。该论文将WMMSE算法应用到多基站多用户的MIMO系统中，存在小区内和小区间干扰，公式最为复杂，复现难度较大。一般情况考虑单基站时，可以在本文给出代码的基础上进行简化即可。

算法核心思想

该算法的核心思想是将加权系统和速率最大化问题等价转化为加权和均方误差最小化问题，将一个低维度中难以直接发射波束转化为高维度中，迭代优化发射波束、接收波束 以及权重矩阵 ，而三个子问题中优化发射波束和权重矩阵是凸优化问题，可以直接求一阶导，得到子问题的最优解，迭代求解发射波束时因为含有拉格朗日对偶变量，因此需要借助二分查找法来寻找最优的对偶变量大小，这是算法实现最复杂的部分，而优化接收波束矩阵是一个经典的最小均方误差接收机设计的问题，可以直接得到闭式解，因此，迭代优化三个变量，直至收敛即可。

该算法的具体推导过程，可以仔细阅读论文或者网上也有较多讲解的文章，如：加权最小均方误差(WMMSE)算法，多用户预编码设计-WMMSE方法。本文就不在赘述复杂的推导过程。其算法伪代码如下：

 

WMMSE算法伪代码

 复现代码

仿真参数

clc;clear;
K = 4; % 基站个数
T = 3; % 发射天线个数
R = 2; % 接收天线个数
epsilon = 1e-3; % 收敛条件
sigma2 = 1; % 噪声功率
snr = 25; % 信噪比
P = db2pow(snr)*sigma2; % 发射功率

I = 2; % 每个基站服务的用户个数
alpha1 = ones(I,K); % 权重系数，都假设相同

d = R; % 假设每个用户有R路独立的数据流

max_iter = 100;

 产生信道

信道系数服从复高斯分布 ，由于该论文考虑的多基站多用户场景，因此使用Cell数据结构来保存数据，采用高维矩阵也可以。

H = cell(I,K,K); % 信道系数
for i=1:I
    for k = 1:K
        for j=1:K
           H{i,k,j}=sqrt(1/2)*(randn(R,T)+1i*randn(R,T));
        end
    end
end

 WMMSE算法

根据论文，三个变量的维度为，，，其中是接收天线维度，是发射天线维度，是一个用户的多路复用维度。

rate = []; % 初始化一个空向量记录rate

U = cell(I,K);
U(:)={zeros(R,d)};

% 随机初始化发射波束向量
V = cell(I,K); % 算法第一行
for i=1:I
    for k=1:K
        v = randn(T,d)+1i*randn(T,d); % 随机初始化
        V{i,k}=sqrt(P/I)*v/norm(v,"fro");
    end
end 

% 求初始化发射波束V后求系统和速率
rate_old = sum_rate(H,V,sigma2,R,I,K,alpha1);
rate = [rate rate_old];

iter1 = 1;
while(1)
    U = find_U(H,V,sigma2,R,I,K,d); % Tbale I line 4 in p.4435
    W = find_W(U,H,V,I,K,d); % Tbale I line 5 in p.4435
    V = find_V(alpha1,H,U,W,T,I,K,P); % Tbale I line 6 in p.4435
    rate_new = sum_rate(H,V,sigma2,R,I,K,alpha1);
    rate = [rate rate_new];
    iter1 = iter1 + 1;
    if abs(rate_new-rate_old) / rate_old < epsilon || iter1 > max_iter
        break;
    end
    rate_old = rate_new;
end

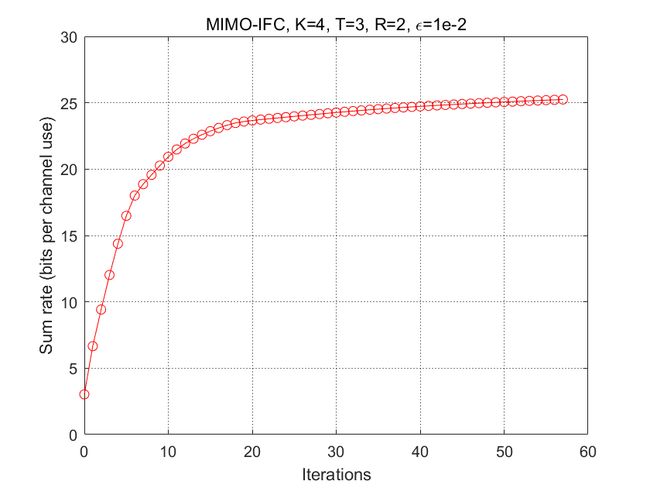
plot(0:iter1-1,rate,'r-o')
grid on
xlabel('Iterations')
ylabel('Sum rate (bits per channel use)')
set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1)
title('MIMO-IFC, K=4, T=3, R=2, \epsilon=1e-3','Interpreter','tex')
%title('SISO-IFC, K=3, T=1, R=1, \epsilon=1e-3','Interpreter','tex')

 子函数（优化接收矩阵U）

function U = find_U(H,V,sigma2,R,I,K,d)
    J = cell(I,K);
    J(:)={zeros(R,R)};
    U = cell(I,K);
    U(:)={zeros(R,d)};
    for i=1:I
        for k=1:K
            for j=1:K
                for l=1:I
                    J{i,k} = J{i,k} + H{i,k,j}*V{l,j}*(V{l,j}')*(H{i,k,j}'); % 算法Table I, 第四行括号求和的部分
                end
            end
            J{i,k} = J{i,k} + sigma2*eye(R); % 算法Table I, 第四行括号求和加上噪声项的部分
            U{i,k} = J{i,k}\H{i,k,k}*V{i,k}; % 算法Table I, 第四行括号求逆，然后乘以H乘以V
        end
    end     
end

 子函数（优化权重矩阵W）

function W = find_W(U,H,V,I,K,d)
    W = cell(I,K);
    W(:) = {zeros(d,d)};
    for i=1:I
        for k=1:K
            W{i,k} = inv(eye(d)-U{i,k}'*H{i,k,k}*V{i,k}); % 算法Table I, 第五行
        end
    end
end

 子函数（优化发射波束V）

function V = find_V(alpha1,H,U,W,T,I,K,P)
    V = cell(I,K);
    A = cell(K);
    A(:) = {zeros(T,T)};
    

    for k=1:K   % 公式15括号内求和部分     
        for j=1:K
            for l=1:I
                A{k} = A{k} + alpha1(l,j)*H{l,j,k}'*U{l,j}*W{l,j}*(U{l,j}')*H{l,j,k};
            end
        end   
    end 
    
    max_iter = 100; % 二分法查找最优对偶变量\mu
    mu = zeros(K,1);
    for k=1:K % 对每个基站迭代寻找最优\mu
        mu_min = 0;
        mu_max = 10;
        iter = 0;
        while(1)
            mu1 = (mu_max+mu_min) / 2;
            P_tem = 0;
            for i=1:I % 计算功率和
                V_tem = inv((A{k}+mu1*eye(T)))*alpha1(i,k)*((H{i,k,k}')*U{i,k}*W{i,k}); % 公式15
                P_tem = P_tem + real(trace(V_tem*V_tem'));
            end
            if P_tem > P
                mu_min = mu1;
            else
                mu_max = mu1;
            end
            iter = iter + 1;

            if abs(mu_max - mu_min) < 1e-5 || iter > max_iter
                break
            end
        end
        mu(k) = mu1;
    end

    for i=1:I
        for k=1:K
            V{i,k} =  inv((A{k}+mu(k)*eye(T)))*alpha1(i,k)*((H{i,k,k}')*U{i,k}*W{i,k}); % 公式15
        end 
    end 
end

 子函数（计算系统和速率sum_rate）

function system_rate = sum_rate(H,V,sigma2,R,I,K,alpha1)
    rate = zeros(I,K);
    for i=1:I
        for k = 1:K
            temp = zeros(R,R);
            for l=1:I
                for j=1:K
                    if l~=i || j~=k
                        temp = temp + H{i,k,j}*V{l,j}*(V{l,j}')*(H{i,k,j}');
                    end
                end
            end
            rate(i,k) = log2(det(eye(R)+H{i,k,k}*V{i,k}*(V{i,k}')*(H{i,k,k}')*inv(temp + sigma2*eye(R)))); % 公式2
        end
    end
    system_rate = real(sum(rate.*alpha1,'all'));
end

仿真结果

论文中图1(a)，场景为K=3，R=1，T=1

图1（a）复现结果

单天线论文原图

论文中图1(b)，场景为K=4，R=3，T=2

图1（b）复现图

 

多天线论文原图

总结

WMMSE算法复现还是需要对算法有深度的理解，特别是多基站多用户的场景，公式复杂，写代码时稍不注意就会出错，因为将代码分享出来，供大家交流学习，希望对大家科研学习有帮助。

希望多点赞收藏关注，评论或私信交流！~