相关性分析【用python&pandas实现】

相关分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个因素的的相关密切程度，相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。

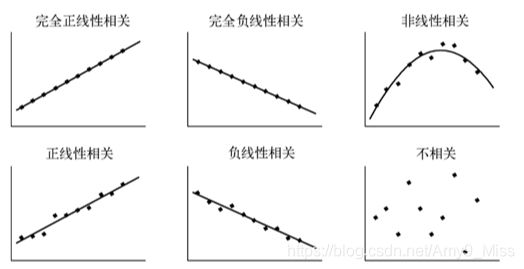
判断数据之间的关系，常用的方法有两种：散点图和相关关系。

散点图

散点图：是判断数据是否具有相关关系最直观的方法。

相关系数

相关系数是反映两个变量之间线性相关程度的指标（相关系数的平方称为判定系数）

常用的衡量变量间相关性的方法主要有三种：

• Pearson相关系数：即皮尔逊相关系数，用于衡量两个连续性随机变量间的相关系数。
• Spearman相关系数：即斯皮尔曼相关系数，是一种秩相关系数。根据原始数据的排序位置进行求解，也被定义为等级变量之间的Pearson相关系数。
• kendall相关系数：即肯德尔相关系数，也是一种秩相关系数，常计算的对象是有序分类变量。

以上三种方法反应的都是两个变量之间变化趋势的方向以及程度，取值范围为[-1, 1]。当接近1时，表示两者具有强烈的正相关性；当接近-1时，表示有强烈的的负相关性；而值接近0，则表示相关性很低。

Pearson相关系数（Pearson Correlation Coefficient）

当两个变量都是正态连续变量，且两者之间呈线性关系时，则可以用Pearson来计算相关系数。取值范围[-1,1]。计算公式如下

公式一：
$$\begin{array}{rl}{\rho }_{X,Y}& =\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}\\ & =\frac{E((X-{\mu }_X)(Y-{\mu }_Y))}{{\sigma }_X{\sigma }_Y}\\ & =\frac{E(XY)-E(X)E(Y)}{\sqrt{E(X^2)-E^2(X)}\sqrt{E(Y^2)-E^2(Y)}}\end{array}$$
公式二：
$${\rho }_{X,Y}=\frac{N\sum x_i{y}_i-\sum x_i\sum y_i}{\sqrt{N\sum x_i^2-(\sum x_i{)}^2}\sqrt{N\sum y_i^2-(\sum y_i{)}^2}}$$
公式三：
$${\rho }_{X,Y}=\frac{\sum (x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum (x_i-\overline{x}{)}^2\sum (y_i-\overline{y}{)}^2}}$$
以上三个公式是等价的，其中E是数学期望，$cov(X,Y)$是X,Y的协方差，${\sigma }_X$是X的标准差，${\mu }_X$是X的期望E(X)，N是数据量。

通过相关系数绝对值范围来判断变量的相关强度：

• 0.8-1.0 极强相关
• 0.6-0.8 强相关
• 0.4-0.6 中等程度相关
• 0.2-0.4 弱相关
• 0.0-0.2 极弱相关或无相关

采用Pearson相关系数检验相关性时，应先检验数据是否服从正态分布：

import numpy as np
import pandas as pd
from scipy import stats

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data3 = pd.Series(np.random.rand(100)*20).sort_values(ascending=False)
data = pd.DataFrame({'X':data1.values,
                     'Y':data2.values,
                     'Z':data3.values,})

# 正态性检验
u1,u2,u3 = data['X'].mean(),data['Y'].mean(),data['Z'].mean()  # 计算均值
std1,std2,std3 = data['X'].std(),data['Y'].std(),data['Z'].std()  # 计算标准差
print('X正态性检验：\n',stats.kstest(data['X'], 'norm', (u1, std1)))
print('Y正态性检验：\n',stats.kstest(data['Y'], 'norm', (u2, std2)))
print('Z正态性检验：\n',stats.kstest(data['Z'], 'norm', (u3, std3)))

# 正态性检验 → pvalue >0.05,则数据服从正态分布
# pearson相关系数:
## data.corr(method='pearson', min_periods=1) method默认pearson
## method : {‘pearson’, ‘kendall’, ‘spearman’} 

print("相关系数矩阵:\n",data.corr() ) # 给出相关系数矩阵

# 计算"X"与"Y"之间的相关系数
print('\n计算"X"与"Y"之间的相关系数:',data["X"].corr(data["Y"]))

# 给出Y变量与其他变量之间的相关系数
print("\nY变量与其他变量之间的相关系数:\n",data.corr()["Y"])

正态性检验结果如下：

Pearson相关系数矩阵，结果如下：

根据原理实现Pearson相关系数

# 制作Pearson相关系数求值表
data['(x-u1)*(y-u2)'] = (data['X'] - u1) * (data['Y'] - u2)
data['(x-u1)**2'] = (data['X'] - u1)**2
data['(y-u2)**2'] = (data['Y'] - u2)**2
print(data.head())
print('------')

# 求出r，|r| > 0.8 → 高度线性相关
r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print('Pearson相关系数为：%.4f' % r)

运行结果如下：

可以看到，X与Y的Pearson相关系数与直接调用pandas包得到的结果一致。

Spearman相关系数

Spearman相关系数，又称秩相关系数，根据随机变量的等级而不是其原始值衡量相关性的一种方法。

对原始变量的分布不作要求，适用范围更广些。不服从正态分布的变量、分类或等级变量之间的关联性可采用Spearman秩相关系数 。计算公式如下：
$$r_s=1-\frac{6{\sum }_{i=1}^n(R_i-Q_i{)}^2}{n(n^2-1)}$$
对两个变量成对的取值分别按照从小到大（或者从大到小）顺序编秩，$R_i$代表$x_i$的秩次，$Q_i$代表$y_i$的秩次，$R_i-Q_i$为$x_i、y_i$的秩次之差，n为样本量。

在实际操作中，检验非正态分布变量的相关性可直接调用Spearman方法。

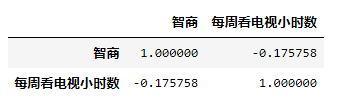
import pandas as pd

data = pd.DataFrame({
    '智商':[106,86,100,101,99,103,97,113,112,110],
    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})

data.corr(method='spearman')

Spearman相关系数矩阵，结果如下：

根据原理实现Spearman相关系数

# “智商”、“每周看电视小时数”重新按照从小到大排序，并设定秩次index
data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)

# 求出di，di2
data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2

# 求出rs
n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Spearman相关系数为：%.4f' % rs)

运行结果如下

可以看到，根据原理实现的结果，与直接调用pandas包得到的结果一致。

Spearman相关系数的计算可以由计算pearson系数的方法，只需要把原变量中的原始数据替换成其在变量中的等级顺序， 然后求替换后的两个变量的Pearson相关系数即可 :

data['range1'].corr(data['range2'],method='pearson').round(4)
# 运行结果为-0.1758，与spearman计算结果一致

运行结果

kendall相关系数

kendall相关系数，也是一种秩相关系数，将数据按某列排序，其他列数据通常是乱序的。它所计算的对象是分类变量。分类变量可以理解成有类别的变量，可以分为

• 无序的，比如性别（男、女）、血型（A、B、O、AB）；

• 有序的，比如肥胖等级（重度肥胖，中度肥胖、轻度肥胖、不肥胖）。

通常需要求相关性系数的都是有序分类变量。

kendall相关系数为同序对§与异序对（总对数减去同序对数为异序对数）之差与总对数的比值。公式如下：
$$r=\frac{P-(n\ast (n-1)/2-P)}{n\ast (n-1)/2}=\frac{4P}{n\ast (n-1)}-1$$

• 如果两个变量排名是相同的，系数为1，则两个变量正相关；

• 如果两个变量排名完全相反，系数为-1，则两个变量负相关；

• 如果排名是完全独立的，系数为0。

示例

假如有一组8人的身高和体重，具体数据如下：

人名	身高排名	体重排名
A	1	3
B	2	4
C	3	1
D	4	2
E	5	5
F	6	7
G	7	8
H	8	6

可以看到，两个排名之间的相关性，可以用kendall计算相关系数。A最重，但体重排名为3，比体重排名为4,5,6,7,8的重，贡献5个同序对，即AB，AE，AF，AG，AH。同理，发现B、C、D、E、F、G、H分别贡献4，5，4，3，1，0，0个同序对。因此，同序对数

$$P=5+4+5+4+3+1+0+0=22$$
则kendall相关系数为
$$R=\frac{4P}{n\ast (n-1)}-1=\frac{4\ast 22}{8\ast 7}-1=0.57$$
结果显示出强大的排名之间的规律，符合预期。

使用kendall相关性系数场景，如评委对选手的评分（优、中、差等），衡量两个（或者多个）评委对几位选手的评价标准是否一致；或者检验各个医院对尿糖的化验结果是否一致；

pandas中直接调用kendall方法，具体代码如下：

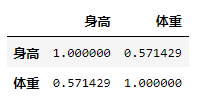
data = pd.DataFrame({'人名':['A','B','C','D','E','F','G','H'],
                    '身高':range(1,9),
                    '体重':[3,4,1,2,5,7,8,6]})
data.corr(method='kendall')

运行结果

根据原理实现kendall相关系数

data = pd.DataFrame({'人名':['A','B','C','D','E','F','G','H'],
                    '身高':range(1,9),
                    '体重':[3,4,1,2,5,7,8,6]})
# 同序对数，前提是 身高列已升序排序
n = data.shape[0]  # 样本数据量
s =[]
for i in range(n):
    tmp =np.sum([1 for j in range(i+1,n) if data.loc[j,'体重']-data.loc[i,'体重'] >0])
    s.append(tmp)
P = sum(s)  
r = 4*P/(n*(n-1))-1
r

运行结果：

可以看到，根据原理实现的结果，与直接调用pandas包得到的结果一致。

一般地，利用相关系数来挑选模型的变量。最常规的方式是先计算所有字段与因变量的相关系数，把相关系数较高的放入模型。然后计算自变量之间的相关系数，若自变量间的相关系数高（一般大于0.8），说明存在多重共线性，需要进行删减，保留其中一个即可。

参考链接

pandas相关系数函数corr()

相关性分析

如果本文对你有帮助，记得“点赞”哦~