EMA - 指数移动平均
EMA 基本概念见 Wikipedia,本文不赘述。
基本公式
S[0] = Y[0]
S[i] = Y[i] * alpha + S[i-1] * (1 - alpha)其中 alpha 为平滑因子,数值越小曲线越平滑
要点
初始值 S1 会引入误差,为了消除误差有几种常见策略:
- 取前 N 个值的均值作为 S1
- 迭代的前 N 次使用动态平滑因子 alpha,从 1 逐渐变为设定值。
- 系统空转 N 次( ‘spin-up’ interval)之后再对外提供服务
如何选择 alpha?
- 这是应用决定的,并没有固定的规则。
- 一种选择alpha 的思路是使得均方差最小,数据最平滑。
- 你也可以有自己的策略(思考:你真的需要特别平滑吗?)
一种自适应的计算 alpha 的方法
S[i] 可以写作:
S[n] = w[n] * Y[n] + w[n-1] * Y[n-1] + w[n-2] * Y[n-2] + … w[1] * Y[1] + w[0] * Y[0]
Y 值是随机序列,我们无法预知。每个 Y 的权重 w 和 alpha 相关,是可以预先计算出来的。什么意思呢?分述如下:
我们没有办法控制 Y[i] 在 S[n] 中的占比,因为 Y[i] 是一个输入序列,我们无法预先知道它的值。举个例子
设
Y[0] = Y[1] = … = Y[n - k - 1] = 1;
Y[n - k] = Y[n - k + 1] = … = Y [n - 1] = Y[n] = 0有:
S[n] = w[n - k - 1] * Y[n - k - 1] + … w[1] * Y[1] + w[0] * Y[0]
可知无论 w (w > 0 )为多少,Y[0], Y[1], … , Y[n - k - 1] 在 S[n] 中占比 100%。
但是,我们可以控制 最后 k 个值的权重在总权重里的占比。>>参考文档<<
最后k个权重之外的权重和 / 总权重
= (w[n-k] + w[n-k-1] + w[n-k-2] + …. ) / 1
= a * ( 1 - a)^k + a * (1 - a)^(k+1) + ….
= a * (1-a) ^k * [ 1 + (1-a) + (1-a)^2 + …..]
= (1-a)^k第四步到第五步,数学不太好的同学注意:当 1 > a > 0, n->无穷时,
a * [ 1 + (1-a) + (1-a)^2 + …..] = 1
如果我们希望最近 k 步之前的权重占比为 10%,最近 k 步权重占比 90%,根据上面的公式有:
0.1 = (1 - a) ^k
则有: a = 1 - e^(ln0.1 / k)
再看一个最近 k 步之前的权重值为一个特殊值的例子: e^-1。
我们希望最近 k 步之前的权重占比为 e^-1 = 0.3678,最近 k 步权重占比 1- e ^ -1 = 0.6321,根据上面的公式有:
e ^ -1 = (1 - a) ^k
则有: a = 1 - e^(-1 / k)
k-alpha 对照表:
| k | a |
|---|---|
| 1 | 0.6321 |
| 2 | 0.3934 |
| 3 | 0.2834 |
| 4 | 0.2212 |
| 5 | 0.1813 |
| 10 | 0.095 |
| 20 | 0.049 |
| 30 | 0.033 |
| 40 | 0.025 |
| 50 | 0.020 |
| 100 | 0.010 |
| 200 | 0.005 |
设采样周期为 interval,采样窗口为 window,那么窗口内共采样 window / interval 次。
设 k = window / interval。
则有 a = 1 - e ^ ( -1 / (window / interval)) = 1 - e ^ (- interval / window)
在这种情况下,最近 2k 步权重占比为多少呢?
1 - 忽略的权重 / 总权重 = 1 - (1-a)^2k = 1 - e ^ -2 = 1 - 0.1353 = 0.8647
对照表:
| step | weight |
|---|---|
| k | 0.6321 |
| 2k | 0.8647 |
| 3k | 0.9502 |
| 4k | 0.9816 |
从应用的角度看,这意味着什么呢?
假设我们的 window 是 1 天,那么最近一天的权重占比 63%,最近 2 天的权重占比 86%,三天 95%,四天 98%,等等。这意味着四天之外的权重影响力只占到 2%。还啰嗦一句,这里是“权重影响力”,并不是”数据影响力“,w 和 Y 是两码事。如果 四天之外的数据特别大或者特别小,对当前计算出来的值影响还是会很大的。
最后附几个例子。
图中,每个格子是 100 * 100, 红色部分为 EMA曲线。
数据特征永久变化,interval = 100,window = 100,alpha = 0.2834

连续数日数据特征变化,后恢复,interval = 100,window = 100,alpha = 0.2834
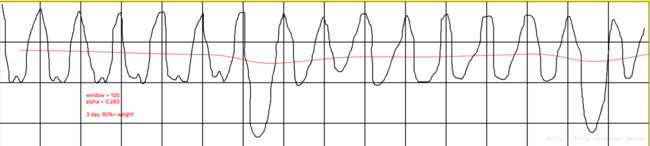
某日数据突变,后恢复,interval = 100,window = 100,alpha = 0.2834
EMA 几乎跟随数据变化,interval = 1,window = 1,alpha = 0.033
在线感受一下EMA曲线和参数之间的关系吧:http://reactshare.cn/ema

