PyTorch指数移动平均(EMA)手册
文章目录
- PyTorch指数移动平均(EMA)手册
-
- EMA的数学模型
- EMA的意义
- EMA的偏差修正
- EMA在测试阶段的优越性能
- PyTorch实现
- Reference
PyTorch指数移动平均(EMA)手册
指数移动平均 —— Exponential Moving Average (a.k.a Exponentially Weighted Moving Average, EMA)
指数移动平均EMA是用于估计变量的局部均值的,它可使变量的更新不只是取决于当前时刻的数据,而是加权平均了近期一段时间内的历史数据值,使得变量的更新更平滑,不易受某次异常值的影响。
EMA的数学模型
借用吴恩达课程的例子,假设有 n n n天的温度(temperature)数据: [ θ 0 , θ 1 , . . . , θ n ] [\theta_0, \theta_1, ..., \theta_n] [θ0,θ1,...,θn],若我们要预测温度的变化趋势(即温度的局部平均值), t t t天内温度数据的直接平均数可以计算为: 1 t ∑ i = 1 t α i \frac{1}{t}\sum_{i=1}^{t}\alpha_i t1∑i=1tαi,这样我们就可以大致知道这 t t t天内平均温度是多少了。但这样做的方法有缺点,例如,我们需要记录下 t t t天的所有数据,如果 t t t较大,记录数据占用的内存是比较大的,计算效率也较低;此外,如果 t t t较大,若在这 t t t天内有明显的离群值(某一天的温度不符合这 t t t天的整体变化趋势),那么最终的计算结果也会受较大的影响,或者 t t t天内温度变化飘忽不定,那么预测曲线将会是上下动荡的。
而指数移动平均模型就是每获取一个新数据,就将其跟历史数据加权平均一下,其数学公式为:
v t = β ∗ v t − 1 + ( 1 − β ) ∗ θ t v_t = \beta * v_{t-1} + (1 - \beta) * \theta_t vt=β∗vt−1+(1−β)∗θt
其中 v t v_t vt代表前 t t t天的温度加权均值, β ∈ [ 0 , 1 ) \beta \in [0, 1) β∈[0,1)为前 t − 1 t-1 t−1天温度加权均值(历史数据)的权重, θ t \theta_t θt代表第 t t t天的温度数据。
EMA的意义
从公式可以看出,EMA模型的意义就是加权平均历史数据,从而得到估计的平均值,注意它并不是实际的加权平均值,因为实际权重一般是不可知的,这里的权重 β \beta β是人为设定的。
有种粗略的说法:EMA模型可以近似看成是前 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个历史时刻的 v v v值的平均,下面具体分析下:
我们对EMA公式展开一下,可以得到:
v t = β ∗ v t − 1 + ( 1 − β ) ∗ θ t = ( 1 − β ) ∗ θ t + β ∗ ( β ∗ v t − 2 + ( 1 − β ) ∗ θ t − 1 ) = ( 1 − β ) ∗ θ t + β ∗ ( 1 − β ) ∗ θ t − 1 + β 2 ∗ ( β ∗ v t − 3 + ( 1 − β ) ∗ θ t − 2 ) = ( 1 − β ) ∗ θ t + β ∗ ( 1 − β ) ∗ θ t − 1 + β 2 ∗ ( 1 − β ) ∗ θ t − 2 + β 3 ∗ ( β ∗ v t − 4 + ( 1 − β ) ∗ θ t − 3 ) . . . = ( 1 − β ) ∗ θ t + β ∗ ( 1 − β ) ∗ θ t − 1 + β 2 ∗ ( 1 − β ) ∗ θ t − 2 + β 3 ∗ ( 1 − β ) ∗ θ t − 3 + β 4 ∗ ( 1 − β ) ∗ θ t − 4 + . . . \begin{aligned} v_t &= \beta * v_{t-1} + (1 - \beta) * \theta_t \\ &= (1 - \beta) * \theta_t + \beta * (\beta * v_{t-2} + (1 - \beta) * \theta_{t-1}) \\ &= (1 - \beta) * \theta_t + \beta * (1 - \beta) * \theta_{t-1} + \beta^2 * (\beta * v_{t-3} + (1 - \beta) * \theta_{t-2}) \\ &= (1 - \beta) * \theta_t + \beta * (1 - \beta) * \theta_{t-1} + \beta^2 * (1 - \beta) * \theta_{t-2} + \beta^3 * (\beta * v_{t-4} + (1 - \beta) * \theta_{t-3}) \\ &... \\ &= (1 - \beta) * \theta_t + \beta * (1 - \beta) * \theta_{t-1} + \beta^2 * (1 - \beta) * \theta_{t-2} + \beta^3 * (1 - \beta) * \theta_{t-3} + \beta^4 * (1 - \beta) * \theta_{t-4} + ... \end{aligned} vt=β∗vt−1+(1−β)∗θt=(1−β)∗θt+β∗(β∗vt−2+(1−β)∗θt−1)=(1−β)∗θt+β∗(1−β)∗θt−1+β2∗(β∗vt−3+(1−β)∗θt−2)=(1−β)∗θt+β∗(1−β)∗θt−1+β2∗(1−β)∗θt−2+β3∗(β∗vt−4+(1−β)∗θt−3)...=(1−β)∗θt+β∗(1−β)∗θt−1+β2∗(1−β)∗θt−2+β3∗(1−β)∗θt−3+β4∗(1−β)∗θt−4+...
可以看到, k k k时刻的温度数据的权重项为 β t − k ∗ ( 1 − β ) \beta^{t-k} * (1-\beta) βt−k∗(1−β),当 β t − k = β 1 / ( 1 − β ) \beta^{t-k} = \beta^{1/(1 - \beta)} βt−k=β1/(1−β)时,根据下表数据可知,此时 β t − k ≈ 1 e ≈ 0.368 \beta^{t-k} \approx \frac{1}{e} \approx 0.368 βt−k≈e1≈0.368,即估计的 t t t天的平均温度数据中,第 k = t − 1 / ( 1 − β ) k=t-1/(1-\beta) k=t−1/(1−β)天的温度数据的权值大约为 1 3 ( 1 − β ) \frac{1}{3}(1-\beta) 31(1−β),( β = 0.9 \beta=0.9 β=0.9时这个权值约等于0.0333),更早之前时刻的温度数据的权值都会小于第 k k k天数据的权值,粗略计算地话可以忽略 k = t − 1 / ( 1 − β ) k=t-1/(1-\beta) k=t−1/(1−β)天前的温度数据对第 t t t天温度数据的估计的影响了,因此就粗略地验证了”EMA模型可以近似看成是前 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β)个历史时刻的 v v v值的平均“的说法了,当然,这种说法跟这种验证方法都不是严格数学上的,仅作为理解。
| α \alpha α | 0.1 | 0.01 | 0.001 |
|---|---|---|---|
| ( 1 − α ) 1 α ≈ 1 e ≈ 0.368 (1-\alpha)^{\frac{1}{\alpha}} \approx \frac{1}{e} \approx 0.368 (1−α)α1≈e1≈0.368 | 0. 9 10 ≈ 0.350 0.9^{10} \approx 0.350 0.910≈0.350 | 0.9 9 100 ≈ 0.366 0.99^{100} \approx 0.366 0.99100≈0.366 | 0.99 9 1000 ≈ 0.368 0.999^{1000} \approx 0.368 0.9991000≈0.368 |
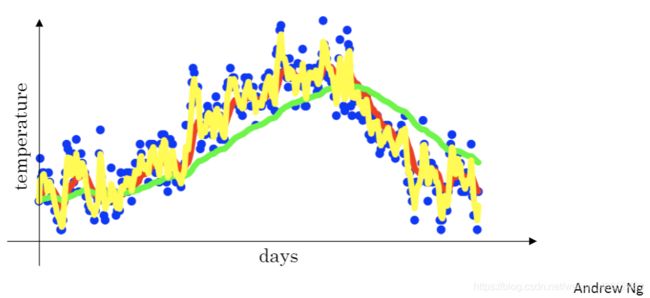
因此,从 β \beta β的具体取值来看:当 β \beta β取值0.5时,EMA模型就相当于近似平均了 1 / ( 1 − 0.5 ) = 2 1/(1-0.5)=2 1/(1−0.5)=2天内的历史数据(如下图黄色曲线);当 β \beta β取值0.9时,EMA模型就相当于近似平均了 1 / ( 1 − 0.9 ) = 10 1/(1-0.9)=10 1/(1−0.9)=10天内的历史数据(如下图红色曲线);当 β \beta β取值0.98时,EMA模型就相当于近似平均了 1 / ( 1 − 0.98 ) = 50 1/(1-0.98)=50 1/(1−0.98)=50天内的历史数据(如下图黄色曲线);当 β \beta β取值0.999时,EMA模型就相当于近似平均了 1 / ( 1 − 0.999 ) = 1000 1/(1-0.999)=1000 1/(1−0.999)=1000天内的历史数据(未在下图展示,此取值为最常用的取值之一)。可以看出, β \beta β取值越大,预测的曲线将会越平滑,受异常值/变化较大的值的影响也就会越小了;取值越小,就会更贴近与短期内的数据变化。
ps:图为吴恩达课程课件的截图。。。。
EMA的偏差修正
在实际使用中,变量 v t v_t vt的初始值是设置为 v 0 = 0 v_0=0 v0=0的,这一初始化会给早期的迭代带来一些偏差,取 β = 0.98 \beta = 0.98 β=0.98作为例子:
v 0 = 0 v 1 = β ∗ v 0 + ( 1 − β ) ∗ θ 1 = 0.02 θ 1 v 2 = β ∗ v 1 + ( 1 − β ) ∗ θ 2 = 0.018 θ 1 + 0.02 θ 2 \begin{aligned} &v_0 = 0 \\ &v_1 = \beta * v_0 + (1 - \beta) * \theta_1 = 0.02\theta_1 \\ &v_2 = \beta * v_1 + (1 - \beta) * \theta_2 = 0.018\theta_1 + 0.02\theta_2 \end{aligned} v0=0v1=β∗v0+(1−β)∗θ1=0.02θ1v2=β∗v1+(1−β)∗θ2=0.018θ1+0.02θ2
可以看到,由于要乘上一个较小的小数,早期预测的数值都会很小,这肯定会与实际数据有较大的偏差,整体的预测曲线如下图紫色曲线所示,曲线左侧的数值都非常低。与绿色曲线相比,初始化为零会在早期带来一定的偏差,而在持续迭代后,两曲线的变化趋势趋于统一。
图中绿色曲线即是做了偏差修正(Bias Correction)后的预测曲线,具体的做法就是给变量 v t v_t vt除以一个去偏差项 1 − β t 1-\beta^t 1−βt:
v t ∗ = v t 1 − β t v^*_t = \frac{v_t}{1-\beta^t} vt∗=1−βtvt
同样取具体的 β = 0.98 \beta = 0.98 β=0.98值代入理解下:
v 0 = 0 v 1 = β ∗ v 0 + ( 1 − β ) ∗ θ 1 1 − β = 0.02 θ 1 0.02 = θ 1 v 2 = β ∗ v 1 + ( 1 − β ) ∗ θ 2 1 − β 2 = 0.018 θ 1 + 0.02 θ 2 1 − 0.9 8 2 ≈ 0.455 θ 1 + 0.505 θ 2 \begin{aligned} &v_0 = 0 \\ &v_1 = \frac{\beta * v_0 + (1 - \beta) * \theta_1}{1 - \beta} = \frac{0.02\theta_1}{0.02} = \theta_1 \\ &v_2 = \frac{\beta * v_1 + (1 - \beta) * \theta_2}{1 - \beta^2} = \frac{0.018\theta_1 + 0.02\theta_2}{1 - 0.98^2} \approx 0.455\theta_1 + 0.505\theta_2 \\ \end{aligned} v0=0v1=1−ββ∗v0+(1−β)∗θ1=0.020.02θ1=θ1v2=1−β2β∗v1+(1−β)∗θ2=1−0.9820.018θ1+0.02θ2≈0.455θ1+0.505θ2
做了偏差修正后,基本消除了早期预测偏差的影响,当随着迭代次数的增加, β t \beta^t βt项逐渐变小,因此当 t t t足够大时, β t \beta^t βt是趋于零的,去偏差项 1 − β t 1-\beta^t 1−βt是趋于1的,此时偏差修正是没有作用的了。从上图中也可以看到绿色曲线与紫色曲线不断趋于重合。
ps:在机器学习中使用指数移动平均的大部分情况下,一般不会去在意是否做了偏差修正的操作,因为随时间推移不做偏差修正得到的结果也是一样的,所以如果不太关注早期的这种偏差带来的影响,那么完全可以不用做偏差修正的操作(会增加计算量)。
EMA在测试阶段的优越性能
不知何人说过:“使用SGD优化算法训练神经网络时,采用指数移动平均模型在很多应用中都可以在一定程度上提高最终模型在测试数据上的表现,使模型在测试数据上的表现更鲁棒。” (搬运自这里)
简单理解就是:网络训练的迭代次数一般都比较多,假设在迭代了较大的次数 N ≥ 10000 N \ge 10000 N≥10000时保存了模型权重,设EMA模型的 β = 0.999 \beta=0.999 β=0.999,也就是说保存的模型大约加权平均了终止前1000次迭代的网络的权重,网络训练到这个时候已经处于局部极小值点附近了,1000个在局部极小值点附近的不同权重平均一下,得到的最终权重将会更鲁棒。
ps:如何深入理解EMA在测试阶段带来的性能提升,可参考论文“SWA Object Detection”,我觉得思想是差不多的。
PyTorch实现
直接上代码,代码是参考的这个仓库的实现,自己加上了可选的偏差修正的实现。
class EMAModel(nn.Module):
def __init__(self, model, decay=0.999, bias_correction=False, num_updates=0, device=None):
super(EMAModel, self).__init__()
self.module = deepcopy(model).eval()
self.bias_correction = bias_correction
self.num_updates = num_updates
self.decay = decay
self.device = device
if self.device is not None:
self.module.to(device=self.device)
def _update(self, model, update_fn):
with torch.no_grad():
for ema_v, model_v in zip(self.module.state_dict().values(),
model.state_dict().values()):
if self.device is not None:
model_v = model_v.to(device=self.device)
ema_v.copy_(update_fn(ema_v, model_v))
def update(self, model):
if self.bias_correction:
debias_term = (1 - self.decay ** self.num_updates)
self._update(model, update_fn=lambda e, m: (self.decay * e + (1 - self.decay) * m) / debias_term)
self.num_updates += 1
else:
self._update(model, update_fn=lambda e, m: self.decay * e + (1 - self.decay) * m)
def set(self, model):
self._update(model, update_fn=lambda e, m: m)
Reference
- [改善深层神经网络:超参数调试、正则化以及优化] – 2.3~2.5
- 理解滑动平均(exponential moving average)
- SWA Object Detection
- rwightman/pytorch-image-models/timm/utils/model_ema.py