【大规模应用】2021年SC戈登贝尔奖paper思路

2021年SC戈登贝尔奖paper思路

Anton 3: Twenty Microseconds of Molecular Dynamics Simulation Before Lunch

• 效果：64节点 2W4原子基准比通用超级计算机快120倍，512节点在220W原子的核糖体系统上快460倍，使得超过5000万原子成为了可能
• 应用：模拟生物大分子（如蛋白质、DNA、RNA）的行为。
• 配置：Anton3 （专为生物学相关的分子的原子级模拟而设计）

——————————————目前问题——————————————

• 商用平台上8个NVIDIA A100显卡的STMV基准测试中，对于分子模拟，大量GPU核心之间分配计算以及在每个时间步长上整合这些计算结果的成本已经掩盖了跨核心并行化的任何收益
• 太高精度的模拟常用机器达不到 0.2 μs/day 的效果，导致时间尺度上达不到模拟所必需的性能

——————————————优化思路——————————————

• 模拟优化1：将原子间作用力范围化，范围的限制能力随距离迅速衰减，在范围内的原子对单独计算，长程作用力随距离衰减较慢，计算方法是利用原子和规则网格点的有限范围内成对相互作用，网格上卷积后，再利用原子和规则网格点的有限范围内成对相互作用，这种优化是线性增长规模（非二次增长）

• 模拟优化2：数值模拟网格和节点网格相对应，相近的节点分配相近的区域

• 硬件优化1：专用的流水线和通用处理器之间的分工，求力总和的过程通过分布式硬件缩减，非结合力再两种不同的类型的专用管道中计算
  

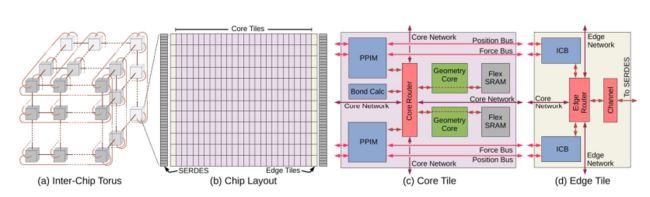
• 硬件优化2：有效的并行化依赖于通信和计算之间的平衡。芯片采用了高度规则的平铺布局，优化了通信和计算，芯片主要由重复的核心瓦片和边缘瓦片组成，核心瓦片排列在芯片中心的12行24列阵列，并包含专用流水线和通用处理器，边缘瓦片位于核心阵列的左右两侧，管理核心瓦片和芯片间3D环面网络之间的通信，整个芯片包含96个片外穿行通道，每个方向29Gbps，提供5.6Tbps的带宽

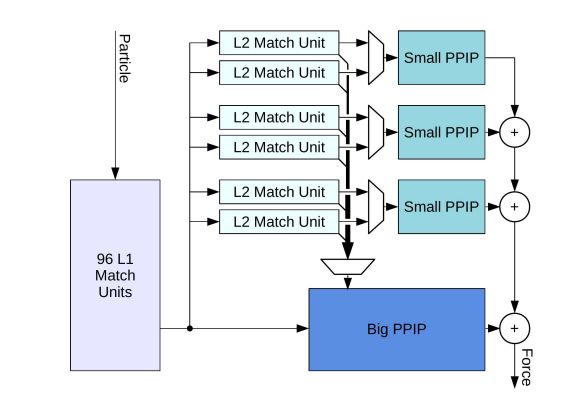
• 硬件优化3：自定义的网络能够带来高带宽和低延迟；原子间力的作用分为大路径的力作用和小路径的力作用，路径宽度相差较大数据精度误差大小大致相等，设置3：1的小：大路径比例，符合硬件结构；

• 算法优化1：通过近似减少计算需求。例如：通过适当的积分算法，每隔一到三秒的时间步计算昂贵的远程力；通过刚性约束消除氢原子高达2.5fs的最快运动允许时间步长（femtoseconds）

• 算法优化2：原来使用中性区域（Neutral Territory，NT）方法计算非结合的、范围有限的力，带宽需求在3D环面互连的所有维度上是不均衡的，每个节点开始计算时需要从其他节点接受整个存储集。设计了Manhattan方法平衡了带宽需求，它允许每个节点在时间步长的最开始就计算其母盒中原子之间的力，无需等待从其他节点接受原子，保证了每一个相互作用都是在节点内计算的。

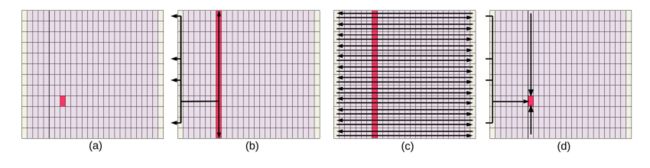
• 时间步长（a）开始，每个核心瓦片保留前一时间步长期间计算的原子位置的子集，通过（b）的2D网状网络广播到列中所有存储集，同时广播到边缘瓦片，当原子到达边缘瓦片（c）时，流过芯片与每个存储集的集合原子相互作用，最终计算结果沿着边缘瓦片返回到发送原子位置的核心瓦片（d），集成完成。

Extreme-Scale Ab initio Quantum Raman Spectra Simulations on the Leadership HPC System in China

• 效果：实现对包含多达3006个原子的实际生物系统的拉曼光谱的快速、准确和大规模并行的全从头模拟，在新一代Sunway高性能计算系统上，双精度性能达到468.5PFLOP/s，混合半精度达到了813.7PFLOP/s
• 应用：拉曼光谱提供了化学和成分信息，可以作为各种材料的结构指纹，包括量子微扰分析和基态计算。
• 配置：新一代Sunway高性能计算系统，MPI，SW26010Pro处理器，双精度14.026TFLOP/s

-> 拉曼效应：将绿光照射到氯仿溶液中，结果发出微弱的黄光，这清楚地表明，一些绿光被溶液中的分子非弹性散射，这种非弹性散射成为拉曼效应，是由光和化学键振动之间的相互作用引起的。因此，可以从光谱中识别材料的化学成分和结构。
——————————————目前问题——————————————

• 拉曼光谱的从头模拟需要计算高达总能量的三阶导数，其中需要同时考虑电场和原子位移微扰的计算，解析能量导致的计算十分复杂。
• 为了获得高精度的结果，需要超越标准密度泛函理论的密度泛函微扰理论（DFPT），可以直接模拟拉曼光谱，但是会破坏周期系统的边界条件，原子位移引起整个基组的变化，因此构造了复杂的矩阵元素。
• 传统局限于小系统，挑战了大系统。

——————————————优化思路——————————————

• FHI-aims是用于计算分子和材料科学的大规模并行软件包，我们描述了一种鲁棒的新算法和FHI-aims的高级实现，使得拉曼光谱的全量子学（QM）计算能够放大到3006个原子的水平。
• 我们使用了FHI-aims包中实现的DFPT模块，除了DFT/DFPT固有的近似以外，没有引入任何QM计算的近似。

——————————————优化方案——————————————
1、 网格划分和三级并行

• 网格划分 ：FHI-aims使用全电子全势数值原子基，全电子原子轨道使用以原子为中心的网格离散化，为了处理被积函数受原子核上的尖点支配的全电子全势系统，这个以原子为中心的网格首先被划分为放射状和角状部分，本工作中所有扰动性质都是在这种离散化的三维物理网格中计算的，这种网格适合于大规模并行实现。
• 网格划分2 ：为了有效地划分非均匀网格，采用网格自适应切面法来形成批次。所有批次都是期望的大小（每批大概100到300个点），集成的负载均衡是根据每个过程中当前点的总和进行分配，新批次总是发送到点数最少的进程。
• 负载均衡：积分计算期间，每个对矩阵元素的一部分进行局部计算，最后合并所有过程的矩阵元素。
• 负载均衡2：在第一次DFT/DFPT迭代中收集每个批次的运行时间和空间位置，并基于位置和运行时间计算批次在过程中的分布，一个流程内各批次之间的距离尽可能小，每批的总运行时间尽可能接近，剩余迭代的批量分布与第一次迭代基本相同，实现自适应负载均衡。
• 三级并行：采用三级并行，（a）极化能力的计算可以用不同的几何图形以令人尴尬的并行方式执行，即第一级并行。由于极化率计算之间不需要通信，我们将整个CPU池分为不同的子组和子通信器。在每个分组中，用DFPT计算极化率。
• 三级并行2：在每次的DFPT计算中，数值积分的计算采用了另外两级并行，DFPT的第一级并行化是在批处理上执行的，这些批处理分布在所有MPI进程中，这使得使用自适应批处理分发算法实现的负载均衡具有良好的并行可伸缩性，DFPT的第二级并行化在一个进程的批处理上执行，线程加速可以进一步提高性能。
  

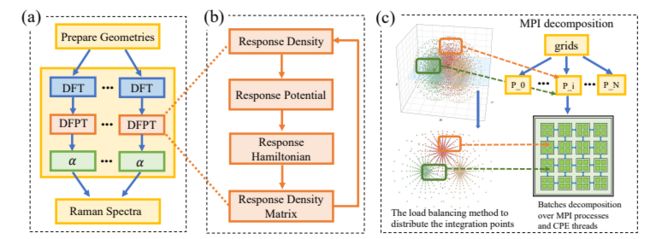
2、 众核优化策略

• 在计算期间进程和线程之间没有通信，我们执行DMA分块来有效地访问主存储器，还采用双缓冲来重叠计算和内存访问。
• 循环平铺是利用循环嵌套中数据访问的空间和时间局限性的一种重要变换，以前的工作展示了将循环平铺模型用于这种基于高速暂存存储器（SPM）的架构。例如在SPM上分配静态空间，应用静态循环分块来保持定期访问数组的快。
• 一个计算机处理单元（CPE）上有两条执行流水线，一条P0支持浮点数和整数类型的标量和矢量化计算操作，一条P1支持标量和矢量化数据加载/存储、比较和跳转操作，以及标量整数操作。这两条线利用双缓冲机制为重叠的数据访问和计算操作提供了优化。
• 为了进一步提高每个内核的计算效率，对函数进行了矢量化处理（SIMD运算），新一代双威CPU提供了一个字向量混洗接口，支持CPE中512位向量寄存器的完全混洗。
• 还提供了并行查找表指令，将LDM分为了16个时隙，每个时隙大小宽度分别为16KB和32Bit，对于寄存器中的一个向量，并行查表的结果由LDM中不同槽的元素组成，而向量加载得到的向量往往由一个连续内存空间中的元素组成。
• 在计算响应势的时候，应用内核融合来减少多核启动的开销。
  
  

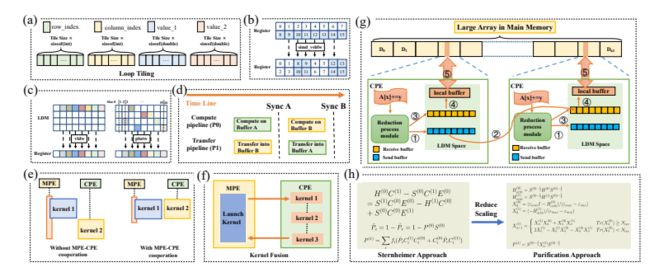
3、 用于获得响应顺序密度矩阵的显式纯化求解器

• 获得响应密度矩阵的传统方法是通过线性方程式隐式求解薛定谔方程（Sternheimer方程）的扰动形式，并且对大规模系统的计算提出了严重的瓶颈。
• 为了减少比例因子，显式纯化方法将Sternheimer方程转化为矩阵-矩阵乘问题，仅涉及零/一阶密度和哈密顿矩阵，根据Kohn的近视原理，密度矩阵和哈密顿矩阵都可以是稀疏的

4、 混合精度计算

• 迭代的DFT/DFPT求解器提供了一个用精度换性能的机会，在内净化循环中，以双倍或者半倍精度迭代执行矩阵-矩阵乘法，然后在外部DFT/DFPT循环期间，可以以令人满意的稳定性和准确性执行不同级别的混合精度。

Billion atom molecular dynamics simulations of carbon at extreme conditions and experimental time and length scales

• 效果：OLCF Summit上的24h 4650节点生产模拟展示了SNAP MD前所未有的扩展性和性能。使用NVIDIA GPUs Kokkos CUDA后端并行效率高于97%，在完整的Summit机器（27900个GPU）实现了50.0 PFLOP/s，峰值性能比之前的量子精确MD高22.9倍。
• 应用：十亿原子分子动力学（MD）使用量子精确的机器学习光谱邻居分析电势（SNAP）在极端压力（12Mbar）和温度（5000K）下观察到长期寻求的碳的高压BC8相。
• 配置：Summit机器（27900个GPU），LAMMPS中使用NVIDIA GPUs Kokkos CUDA后端高效实施的SNAP force内核，使用cuda 11.2.0

-> 十亿个原子的分子动力学模拟：缺乏实验工作的理论和指导，包括对极端PT条件下反应复杂物理的全面原子级理解。使得实验室里重现和探测系外行星核心的高PT环境成为可能。
——————————————目前问题——————————————

• 传统密度泛函理论（DFT）的量子分子动力学（QMD）用于模拟极端PT条件下的物质，由于计算成本限制，目前模拟限于一千个原子的样本和高达几十皮秒的模拟时间。
• SNAP由许多结构不规则深度嵌套的循环组成，这些循环具有不同的小循环大小，与规则结构的线性代数内核（如GEMM）相比，更难优化。

——————————————优化思路——————————————

• 随着机器学习原子间势（ML-IAP18）的出现，能提供具有DFT精度的潜在原子间相互作用的经典描述。我们为碳设计了量子精确的光谱邻域分析势（SNAP）ML-IAP18，它描述了0~50Mbar 和温度高达20000K的极端条件下的特性。精确度在非常严格的QMD结果的5%以内。
• LAMMPS MD模拟包的高效实现允许大规模并行十亿原子模拟。

——————————————优化方案——————————————

1、 Kokkos优化

• 使用Kokkos的二次SNAP ML-IAP的实现和优化，Kokkos提供了一个框架，用于将工作分解成离散的、独立的部分、使用C++编写，映射到后端语言（如CUDA）进行并行分派任务，隐藏了执行工作的特定于架构的细节，Kokkos提供了利用层次并行的结构，最相关的是多维平铺启动，它在概念上映射到CPU上的缓存阻塞以及GPU上的多维线程和块索引。
• Kokkos能在概念上映射到CPU的小内存段，这些内存驻留在缓存中，并映射到GPU上的共享内存。
• SNAP ML-IAP中并行性层次结构的系统提取。通过Kokkos性能可移植框架 “视图” 抽象对多维数据结构的内存布局进行优化。

2、 kernel 分裂

• 将大的kernel分裂成多个小的kernel，降低寄存器压力。
• 大大增加了内存的使用，因为所有原子邻居对的中间量需要在kernel启动之间显示存储，这个促使了指数扁平化，使用压缩的数组代替参差不齐的数组。

3、并行性提取和数据布局优化

• 每个并行性都遵循线性的规律，可以根据需要对每个原子、每个邻居和每个量子数的并行性进行重新排序，能以最大限度地提升性能。
• 简化了数据布局，促进CPU和GPU上的良好的内存访问，其中CPU上的结构数组可促进空间/时间缓存局部性。GPU上的结构数组可以促进内存对齐和合并。所以在原子数量上实现SIMD并行。
• 通过AoSoA数据布局，使得跨架构的理想缓存重用，因为每个矢量化原子集的数据在内存中是连续的，确保了每个缓存页面得到利用。
• AoSoA数据布局自然延伸到工作的层次分块，其中评估可以分组为大到足以使GPU饱和的原子批次，小到足以避免大量内存分配。

4、增加递归多项式求值的算术强度

• 对Wigner U矩阵及其导数的计算的优化，评估递归多项式是一个固有的计算密集型的过程，对于维格纳U矩阵本身，只有复杂的Cayley-Klein参数a和b两个输入，后续的输出都是其递归线性组合。
• 将递归多项式求值重写为混合深度/宽度求值，深度优先与 u${}_j$ 的行，这将中间状态开销降低了一个j系数，促进了缓存重用。
• 将原子积累内联到递归多项式计算中，消除了以后的重新加载。
• 在共享内存中显式缓存中间值。
• 通过引入冗余工作摸型，在计算 u${}_j$ 行的过程中，重新计算一些 u${}_j$’ < j ，从而消除全局内存分段。
• 将x,y,z kernel的评估分成了三个独立的kernel，避免共享存开销的过度增加。

5、二次SNAP中伴随表示的核优化

• 优化伴随矩阵Y的kernel。在线性SNAP的情况下，我们可以通过等式直接将原子添加到Y中，从而绕过Z的中间存储。
• 存储预先计算的Z值，这样以后在Y计算中重用，避免计算z分量的开销。

——————————————具体细节——————————————

AoSoA结构

https://www.dovov.com/cudaarraysarrays.html

Closing the “Quantum Supremacy” Gap: Achieving Real-Time Simulation of a Random Quantum Circuit Using a New Sunway Supercomputer

• 效果：包含111.3万亿个粒子和25亿个网格，获得超过201.1 PFOP/s （双精度）的持续性能，最快运算步长达到298.2 PFLOP/s （双精度），为基于先进超导托克马克（EA3T）实验和中国聚变工程实验堆（cFETR）设计运行状态的2D平衡剖面带来的6D电磁全动力等离子体前所未有的高分辨率演化。
• 应用：使用开发的显式二阶电荷守恒辛电磁粒子（PIc）方案在新一代Sunway超级计算机上模拟圆柱形磁约束环形等离子体。
• 配置：新一代Sunway高性能计算系统，103600个节点，MPI，SW26010Pro处理器，双精度14.026TFLOP/s。

——————————————目前问题——————————————

• 由于磁约束等离子体的多尺度特性，很难应用6D PIC方法进行模拟，需要在极端尺度下对动力学等离子体进行逼真的模拟。

——————————————优化思路——————————————

• 开发的显式二阶电荷守恒辛电磁PIC方案对圆柱形正则网格进行大规模全动力学模拟。可以模拟3072×2048×4096×4320的环形等离子体。带有1.113×10${}^{14}$ 个标记粒子。平均每秒计算精度201.1 PFLOP/s ，峰值性能298.2 PFLOP/s。

——————————————优化方案——————————————

1、 算法优化

• 柱坐标下显式二阶电荷守恒保辛电磁格式

2、 多平台代码生成

• 面对Summit CPU+NVIDIA GPU架构，Sunway 众核处理器架构，tianhe 超级计算机CPU+NUDT矩阵加速器架构，同时支持所有异构平台是一项挑战。
• 因为这些异构平台都有相似的管理工作器（Management Worker，MW）结构，可以用一致的MW编程模型进行编程，传统的多核CPU也可以被视为一种特殊类型的MW节点。
• 开发了一种领域特定语言(DSL)叫做 Parallal SCheme to Many Core（PSCMC），可以描述MW编程模型和相应的代码生成器，是图灵完备的，可以实现任意并行算法， C、 OpenMP、 CUDA、 Sunway Manycore。代码生成过程

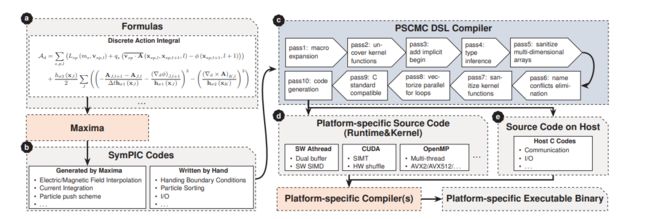
3、 进程级和线程级并行化

• 在大规模实现高并行的关键是提供足够的并行性和平衡的任务划分，使用了希尔伯特空间填充曲线将仿真域划分成小计算快。
• 对粒子进行排序，设计了一个两级粒子缓冲系统，对于其中的每个网格，CB是是一个大小固定的连续存储块，即网格缓冲区，用于存储粒子的位置和速度，对于每个CB，分配一个大小固定的额外存储块，即CB缓冲区，用于对粒子进行排序或者存储CB内某些网格发生溢出的离子，这样大部分粒子被连续存储再内存中，并位于同一块内存

4、粒子排序和自动矢量化

• SIMD单元通常配备进一步提高计算密度，但是测试中，发现现代编译器不能生成汇编代码，而本算法可以有效地使用SIMD指令进行长循环，利用OMP SIMD给出的指令
• 我们设计了一个特定的语法结构来告诉PSCMC编译器使用特定的SIMD内部函数自动矢量化特定的for循环

5、 内存高效优化

• 提供了一种异步DMA传输机制来快速加载数据，为了避免存储器传输延迟，将粒子分组并加载到LDM中的两个缓冲器A、B上，开始双缓冲机制的循环。

6、IO优化

• 在SymPIC中，I/o主要发生在保存字段结果和检查点时。在大规模模拟中，将大量数据写入单个文件将非常耗时，
• 为了在现代集群中利用特定文件系统提供的贷款，设计了一个lightweight IO库，支持任意数量的I/O组，Sunway计算机还配备了一个更小但速度更快的存储系统，利用它输出检查点保存数据。

Closing the “Quantum Supremacy” Gap: Achieving Real-Time Simulation of a Random Quantum Circuit Using a New Sunway Supercomputer

• 效果：模拟器有效地扩展了可模拟rqc的范围，包括10×10(qubits)×(1+40+1)(depth)的电路，具有1.2 EFLOP/s（单精度）或4.4 EFLOP/s（混合精度）的持续性能，相比于Google Sycamore减少了模拟采样时间，从1万年减少到了304秒。
• 应用：开发了一个基于张量的高性能随机量子电路（rqc）模拟器。
• 配置：新一代Sunway高性能计算系统，103600个节点，MPI，SW26010Pro处理器，双精度14.026 TFLOP/s。CPU包括6个核组（CGs），每个核组包括一个管理处理单元（MPE）和一个8×8 的计算处理单元（CPE）

——————————————目前问题——————————————

• 在目前阶段，产生、操纵和测量量子位的技术仍然存在很大的不确定性，

——————————————优化思路——————————————

• 一个近似最优的切片方案，以及一个考虑复杂度和计算密度的路径优化策略。
• 三级并行化方案，可扩展至4200万个内核。
• 融合排列和乘法设计，提高了大范围张量收缩情况（tensor contraction scenarios）下的计算效率。
• 混合精度方案，以进一步提高性能。

——————————————优化方案——————————————

1、 算法优化

• 第一个基于张量的方法采用了PEPS方法，使用投影纠缠对态来表示2D晶格的张量网格量子态，计算复杂度是由底层量子电路决定的。
• 切片能平衡内存需求和可以执行的并行计算数量，通过切片可以进一步减少存储张量的存储器需求，并且可以将原始网格的收缩转换为两个独立收缩子任务，需要寻找一个平衡点在适应MPI进程的内存空间，使所有的并行子任务计算成本增加的可以接受。

2、 寻找算法最佳的收缩路径

• 将最佳收缩路径的定义变成了一个多目标问题，虽然大幅下降计算复杂度很重要，生成更适合底层众核架构的张量排序对实现效率核模拟速度至关重要。
• 应用CoTenGra软件搜索具有损失函数的最佳路径，损失函数结合了计算复杂度和计算密度。

3、 定制的并行化方案

• 切片已经分割成独立的子任务，单个子任务已经触碰单个CG总内存空间的上限了，考虑到额外变量和系统实用程序的额外开销，采用两个CG分配任务进行第二级并行。
• 第三级进一步将张量置换和矩阵乘法分解成不同的计算处理单元CPE进行计算

4、 使用融合排列和乘法的张量收缩

• 张量收缩两个基本步骤：一个是作为预备步骤的张量的指数置换，另一个是下面的矩阵乘法来达到收缩的结果。通常需要排列索引来将张量压缩转换成有效的矩阵乘法，高阶张量的索引的预突变要求数据项之间有步长的移动，这对当前的存储系统是非常不友好的，因此减少或隐藏突变的成本是具有高计算密度的众核处理器上实现有效张量压缩的主要设计问题。
• 对于正常实现的方法，相邻索引只需要一次置换，非相邻则需要多次置换。
• 对于PEPS方法，通常在秩为5~6的张量之间进行收缩，维度大小为32，导致高计算密度。
• 对于这个情况，我们采用不同的CPE以协同执行融合操作，对于CPE的2D阵列，我们指示每一个以不近DMA模式读取对应的数据块，可以以相对较高的DDR带宽利用率获取相应的索引，以矩阵乘为例，可以减少很大一部分DMA加载成本和存储成本，需要精心安排广播方案实现行列总线以及DMA资源的最佳利用。
• 对于优化后的收缩路径，可能遇到秩30与秩4之间的不平衡收缩，以及小得多的维数2，内存为主要制约因素，因此在每个CPE中独立执行融合操作。使用通用转置-转置-GAMM转置的算法实现张量的压缩操作。将置换和乘法融合为一个统一的工作流程。

5、 一种自适应精度缩放的混合精度计算方法

• 经典量子模拟的一个优点是我们没有无法控制的噪音，由于计算单个振幅的独立收缩可以被视为对最终振幅有同等贡献的正交路径。计算分数路径被视为等同于计算保真度f的噪声振幅。因此提出了一个混合精度方案，使用单精度和版精度浮点数来模拟RQC
• 首先我们进行预分析，以检测计算不同部分的精度敏感度，我们执行张量计算的一小部分来评估单精度到半精度转换的灵敏度，
• 其次，我们设计了一种自适应的缩放方法，以便动态调整数据，特别是对精度敏感的部分，从而将误差保持在与单精度计算近似的水平。

——————————————具体细节——————————————

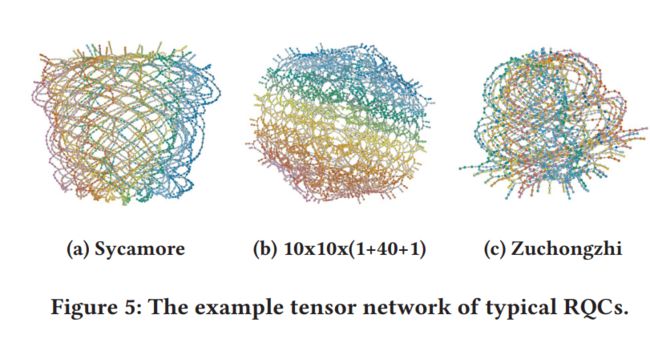
量子电路与张量

在张量类型的方法中，量子电路被描述为张量网络

• 其中一个量子比特的门被描述为秩为2的张量，两个量子比特的门被描述为秩为4的张量
• 一个n-qubit的门，被描述为一个秩为2n的张量
  然后量子电路的模拟被转化成压缩相应张量网络的问题，其中我们执行相应张量的卷积，直到只剩下一个顶点。

问题: 张量方法的直接实现通常会设计复杂性，该复杂性也随着量子位的数量和电路的深度成指数增长，使得大规模电路的模拟难以在合理时间内完成。

->仅通过电路末端进行一个或小批量的状态幅度，来执行模拟，张量网络的复杂性将受到收缩过程中涉及的最大张量的约束，该张量随着与张量网络相对应的图的树宽度呈指数增长。
->随着复杂度的增加，这种方法对于具有大量量子位但深度较浅的电路可能非常有效

->另一种可以集成到基于张量的方法中的技术是来自多体量子物理学的量子态的投影纠缠对态（PEPS）表示，通过使用PEPS作为表示量子态的数据结构，构建了通用量子电路模拟器来模拟

最终，要确定最合适的切片方案，以及由此产生的收缩顺序。

切片方案

切片是一种常用的技术，用于平衡内存需求和我们可执行的并行计算数量，使用heurisitic方法来确定一个优化的切片方案，非常适合大规模并行和底层众核架构.

首先使用基于张量的方法采用了PEPS方法，它使用投影纠缠对态（PEPS）来表示2D晶格的张量网络量子态，采用PEPS方法，RQC模拟的计算复杂度由底层电路决定的，而不是由量子位或门操作的数量决定的。

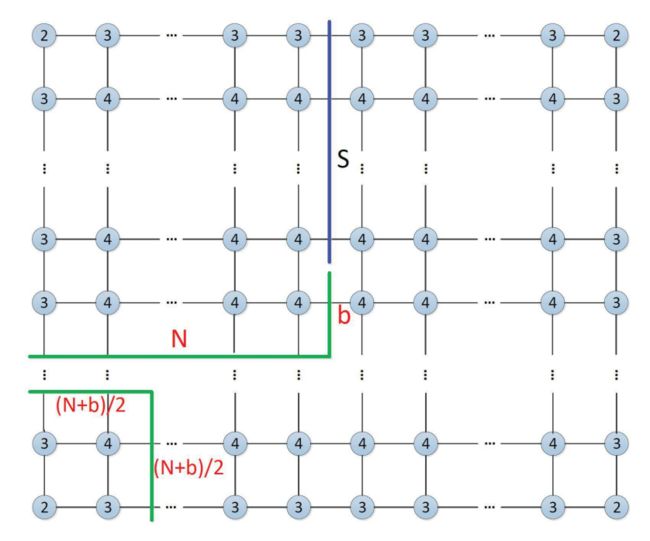
首先，蓝线切断了顶部 行的 超边。

对于 超边的所有可能的 $2^S$ 值，我们可以执行 $2^S$ 切片张量的收缩，其中超边固定为 $2^S$ 可能值之一。

采用切片方法，存储张量的内存需求可以进一步减少（通常在 $2^S$ 的数量级），并且原始网络的收缩可以转换为 $2^S$ 独立的收缩子任务。 因此，切片步骤通常成为大规模并行计算环境执行第一级任务分解的自然方案.

针对 2 × 2 矩形张量网络，我们提出了一种简单直接的启发式方法来识别接近最优的切片方案和收缩顺序（如图 4 所示）。 对于整个收缩过程，我们保持张量的秩不能超过 + 的约束。 的值由 的奇偶性决定（如果 是奇数，我们将 设置为 1，如果 是偶数，则设置为 2）。 通过这样的策略，( + )/2 乘 ( + )/2 平方张量网络可以从左下角收缩，从而得到秩为 + 的张量。 表示为图 4 中的蓝线，我们对 超边进行切片，并将向下收缩的张量的秩保持在 + 内。 这两个张量具有 ( + )/2 连接超边，导致收缩复杂度为 $L^{(3(N+b)/2)}$，其中 = $2^{[d/8]}$ ， 是电路的深度.

为了执行这样的切片，如图 4 所示，切片的超边 的数量可以计算为 = 2 - ( +)/2 - = 3( - )/2。
遵循这样的切片策略，我们可以找到接近最优的收缩顺序，它将计算复杂度保持在(2 ·$L^{(S+3(N+b)/2)}$) = (2 · $L^{3N}$) . 如 [11] 中所述，这种计算复杂度类似于没有切片的最小化空间复杂度的时间复杂度。因此，我们的切片方法在显着降低经典模拟的内存需求的同时，保持了接近最优的计算复杂度。 如图 4 所示，这样的策略可以有效地支持更大尺寸的电路，并使通信和计算之间的配置更加平衡。

寻找最佳收缩路径

在基于张量的方法中，模拟特定样本或一批样本的输出问题变成了相应张量网络的收缩。

最佳收缩路径在超级计算机下定义变成了一个多目标问题，虽然最大限度地降低计算复杂性很重要，但生成更合适底层众核架构的张量排序对于实现效率和模拟速度也至关重要，使用CoTenGra软件来搜索具有损失函数的最佳路径，计算了对计算复杂性和计算密度的考虑。

张量收缩方法

张量收缩有两个步骤：
1、 作为预备步骤的张量的指数置换
2、 下面的矩阵乘法来达到收缩的结果

通常需要排列索引来将张量压缩转换成有效的矩阵乘法。高阶张量索引的排列需要数据项之间的跨步移动，这对当前的存储系统本质上是不友好的。 因此，降低或隐藏置换成本成为在具有高计算密度的众核处理器上实现高效张量收缩的主要设计问题。

对于秩-张量($i_1$,$i_2$,···,,···,,···,$i_m$) 和秩-张量($i_1$,$i_2$,···,,·· · ,, ··· ,$i_n$)，假设我们需要收缩 和 指数。 在分离置换和乘法的正常实现中，如果 和 是相邻索引，那么我们只需要执行一次置换。 否则，我们可能需要多次执行置换，从而导致大量置换开销。

对于基于 PEPS 的方法，我们通常在 5 或 6 级左右的张量和 32 的维度大小之间有收缩，从而导致高计算密度。对于这种情况，我们采用不同的 CPE 以协作的方式执行融合操作。

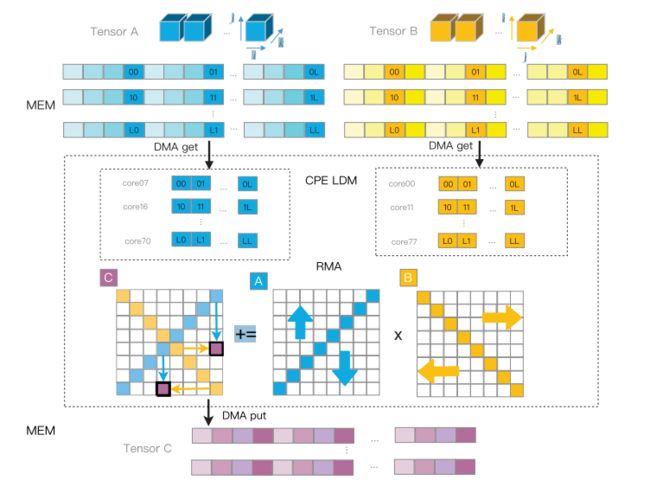
如图 8 所示，对于一个 2D 的 CPE 数组，我们指示它们中的每一个以跨步 DMA 模式读取其对应的数据块，从而以较高的 DDR 带宽利用率获取对应的索引。以张量 A 和 B 为例，经过跨步读取后，将 A 和 B 的对应部分加载到 的CPE 中。之后，我们可以在 CPE 阵列内以协作的方式执行高效的矩阵乘法。我们使用 CPE 阵列的两条对角线作为数据广播器，充分利用片上网络带宽。如图 8 所示，在每一步中，对角线上的每个 CPE 都进行一次广播，将其数据转发到其对应的行或列（A 对角线上的 CPE 沿列广播，B 对角线上的 CPE 沿行广播），然后每个 CPE 执行可用项的子乘法并写回相应的子块。经过子块C的全循环后，矩阵乘法的计算得到最终的结果。

这样，我们以融合的方式完成索引置换和乘法运算，这将减少很大一部分 DMA 加载成本和大部分 DMA 存储成本。 此外，精心调度的对角广播方案实现了行/列总线以及DMA资源的最佳利用，实现了RMA和DMA效率之间的平衡。
对于由 CoTenGra 软件在 Sycamore 模拟中生成的优化收缩路径，我们通常在 30 阶张量和 4 阶张量之间有不平衡的收缩情况，并且维度大小要小得多，为 2。在这种情况下，计算密度 显着下降，内存带宽成为主要制约因素。 在这种情况下，我们在每个 CPE 中独立执行融合操作

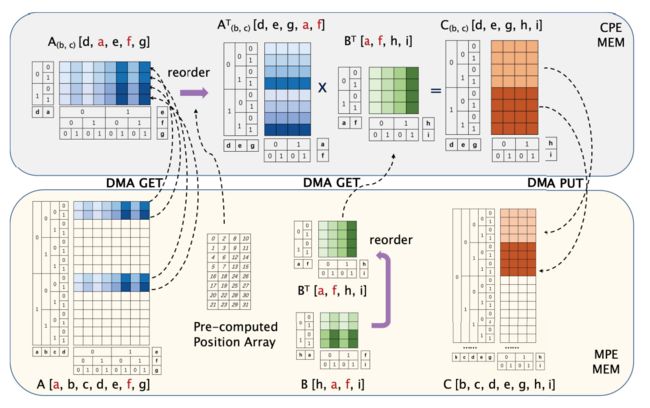
如图 9 所示，我们使用通用 Transpose-Transpose-GEMM Transpose (TTGT) 算法 [28] 实现张量收缩操作，该算法将置换和乘法融合为一个统一的工作流程

让[, , ,, , ,] 是一个具有 = 7 个索引的张量，[ℎ, , ,] 是一个具有 = 4 个索引的张量，每个索引都有两个维度。让 , 成为 = 2 个要收缩的常见指数。设[, , , , , ℎ,] 为收缩积。以 作为较小的张量，我们将其置换为 [, , ℎ,] 并将其存储在 LDM 快速缓冲区中。对于高阶张量，从、、、、、、到、、、、、、的排列分布在不同的CPE上。每个 CPE 使用 DMA 读取最后一个− 索引的连续块，大小为 2−（在本例中 = 5，受 LDM 大小的限制）。阅读位置由剩余索引、、、的新顺序、、、确定。内部索引、、、、到新顺序、、、、的排列可以在LDM内部使用预先计算的位置数组来执行，以避免重复的内存地址计算。然后，我们在 LDM 中应用一个完全优化的 GEMM 内核，以产生索引顺序为 d、e、g、h、i 的 C 的部分结果，并将大小为 2+−2 的连续数据块通过DMA。