菜菜学paddle第六篇:利用LeNet卷积神经网络识别手写数字
前言
LeNet是最早的卷积神经网络之一。1998年,Yann LeCun第一次将LeNet卷积神经网络应用到图像分类上,它通过连续使用卷积和池化层的组合提取图像特征,在手写数字识别任务中取得了巨大成功。
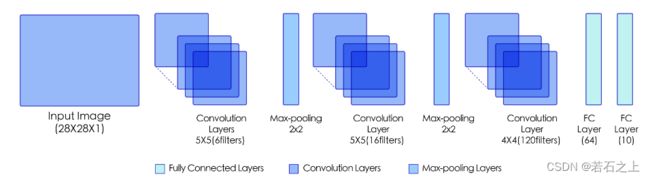
LeNet模型网络结构示意图
模型设计
1、新建文件leNet.py,根据leNet的结构示意图写出对应的代码:
import paddle
from paddle.nn import Conv2D,MaxPool2D,Linear
import paddle.nn.functional as F
class LeNet(paddle.nn.Layer):
def __init__(self, num_classes = 1):
super(LeNet, self).__init__()
self.conv1 = Conv2D(in_channels=1,out_channels=6,kernel_size=5)
self.max_pool1 = MaxPool2D(kernel_size=2,stride=2)
self.conv2 = Conv2D(in_channels=6,out_channels=16,kernel_size=5)
self.max_pool2 = MaxPool2D(kernel_size=2,stride=2)
self.conv3 = Conv2D(in_channels=16,out_channels=120,kernel_size=4)
self.fc1 = Linear(in_features=120, out_features=64)
self.fc2 = Linear(in_features=64,out_features=num_classes)
def forward(self, x):
x = self.conv1(x)
x = F.sigmoid(x)
x = self.max_pool1(x)
x = F.sigmoid(x)
x = self.conv2(x)
x = self.max_pool2(x)
x = self.conv3(x)
x = paddle.reshape(x , [x.shape[0], -1])
x = self.fc1(x)
x = F.sigmoid(x)
x = self.fc2(x)
return x模型训练
1、新建文件:LeNetTrain.py
import numpy as np
import paddle
import paddle.nn.functional as F
from paddle.vision.transforms import ToTensor
from paddle.vision.datasets import MNIST
from leNet import LeNet
def train(model, opt, train_loader, valid_loader):
model.train()
for epoch in range(EPOCH_NUM):
for batch_id,data in enumerate(train_loader()):
img = data[0]
label = data[1]
logits = model(img)
loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
loss = loss_func(logits,label)
avg_loss = paddle.mean(loss)
if batch_id % 2000 == 0:
print("epoch:{},batch_id:{},loss is:{:.4f}".format(epoch,batch_id,float(avg_loss.numpy())))
avg_loss.backward()
opt.step()
opt.clear_grad()
model.eval()
accuracies = []
losses = []
for batch_id, data in enumerate(valid_loader()):
img = data[0]
label = data[1]
# 计算模型输出
logits = model(img)
pred = F.softmax(logits)
# 计算损失函数
loss_func = paddle.nn.CrossEntropyLoss(reduction='none')
loss = loss_func(logits, label)
acc = paddle.metric.accuracy(pred, label)
accuracies.append(acc.numpy())
losses.append(loss.numpy())
print("[validation] accuracy/loss: {:.4f}/{:.4f}".format(np.mean(accuracies), np.mean(losses)))
model.train()
# 保存模型参数
paddle.save(model.state_dict(), 'leNet.mnist.pdparams')
# 创建模型
model = LeNet(num_classes=10)
# 设置迭代轮数
EPOCH_NUM = 5
# 设置优化器为Momentum,学习率为0.001
opt = paddle.optimizer.Momentum(learning_rate=0.001, momentum=0.9, parameters=model.parameters())
# 定义数据读取器
train_loader = paddle.io.DataLoader(MNIST(mode='train', transform=ToTensor()), batch_size=10, shuffle=True)
valid_loader = paddle.io.DataLoader(MNIST(mode='test', transform=ToTensor()), batch_size=10)
# 启动训练过程
train(model, opt, train_loader, valid_loader)
模型验证
1、新建文件LeNetEval.py:
from leNet import LeNet
import numpy as np
import paddle
from paddle.vision.transforms import ToTensor
from paddle.vision.datasets import MNIST
# 创建模型
model = LeNet(num_classes=10)
params_file_path = 'leNet.mnist.pdparams'
param_dict = paddle.load(params_file_path)
# 加载模型参数
model.load_dict(param_dict)
# 定义预测过程
model.eval()
# 加载测试集 batch_size 设为 1
valid_loader = paddle.io.DataLoader(MNIST(mode='test', transform=ToTensor()), batch_size=1)
success = 0
error = 0
for batch_id, data in enumerate(valid_loader()):
img = data[0]
label = data[1]
#预测
logits = model(img)
#转换为整数
label = label.numpy().astype('int32')[0]
#取最大的那个预测概率的下标
result = np.argsort(logits[0])[-1]
if (label == result) :
success = success + 1
else:
error = error + 1
#打印结果
print("本次预测的正确的数量是{}, 错误的数量是{}".format(success, error))2、结果输出:
本次预测的正确的数量是9553, 错误的数量是447
总结:
1、本次进行了5次迭代,预测的准确率就非常高了,超过了95%
2、先画出模型图,然后再编写对应的代码,非常的高效