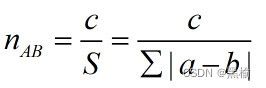空间结构是可数的吗?

移位距离假设

(A，B)---m*n*k---(1,0)(0,1)

用神经网络分类A和B，把参与分类的A和B中的数字看作是组成A和B的粒子，分类的过程就是让A和B中的粒子互相交换位置，寻找最短移位路径的过程。而熵H与最短移位距离S成正比，迭代次数n与S成反比。

移位规则汇总

移位距离就是等位点数值差的绝对值的和S=Σ|a-b|，如果训练集有多张图片取平均值。

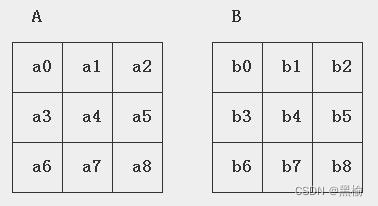
如对一组3*3的矩阵

S=s0+s1+，…，+s8=|a0-b0|+|a1-b1|+,…,+|a8-b8|

(ABC , D )---2*4*2---(1,0)(0,1)

这次继续在多张图片的训练集上验证这一假设，让一个训练集里有3张图片，另一个训练集里有1张图片。如分类01-01-11-01，一个训练集有(0,1),(0,1),(1,1)3张图片，而另一个训练集里只有(0,1)一张图片，进样顺序为

0	1		0	1
0	1		0	1
1	1		0	1

循环往复直到收敛。

实验一共进行了13组

S平均		S			δ	0.01	0.001	9.00E-04	8.00E-04	7.00E-04
0.333333	3	1	b	01-01-11-01	迭代次数n	13432.36	139891.7	157113.9	179519.3	207188.2
0.333333	3	1	b	01-11-11-11	迭代次数n	12676.79	107286.2	117513.9	133028.4	154503.1
0.666667	3	2	b	01-11-10-11	迭代次数n	15719.23	104694.3	114401.5	126914.8	147143.7
1	3	3	b	01-01-10-11	迭代次数n	12799.57	86593.53	94449.04	104090.8	116335.3
0.666667	3	2	b	01-10-10-10	迭代次数n	9729.462	71300.71	81367.92	92317.08	105625.9
0.666667	3	2	b	01-11-11-01	迭代次数n	6608.085	63333.77	71977.75	83191.75	96217.09
0.666667	3	2	b	01-01-11-11	迭代次数n	6267.251	49675.77	55069.35	62602.73	71207.15
0.666667	3	2	b	11-01-01-11	迭代次数n	6198.186	49881.95	55585.57	62915.46	70390.47
1.333333	3	4	b	01-01-10-10	迭代次数n	4923.854	36408.93	40618.85	46367.03	53840.08
1.333333	3	4	b	01-10-01-10	迭代次数n	5078.638	36479.74	40784.88	45512.43	52834.54
1	3	3	b	01-10-11-10	迭代次数n	4718.648	29763.91	33889.95	37498.31	42272.53
1.333333	3	4	b	01-11-11-10	迭代次数n	3028.879	15452.6	17931.25	19334.8	22579.88
1.666667	3	5	b	01-01-11-10	迭代次数n	3010.307	16673.54	17539.43	19642.51	21521.67

其中01-01-11-01的迭代次数最大，01-01-11-10的迭代次数最小，当收敛误差为7e-4的时候最大值几乎是最小值的10倍。01-01-11-01的移位距离为1平均移位距离为0.33

计算过程

						s
0	1		0	1		0
0	1		0	1		0
1	1		0	1		1

因为有3张图片因此平均移位距离是0.33.

0.666667	3	2	b	01-01-11-11	迭代次数n	6267	49676	55069.35	62602.73	71207.15
0.666667	3	2	b	11-01-01-11	迭代次数n	6198	49882	55585.57	62915.46	70390.47

这两组是相同的，表明迭代次数和图片的顺序没有关系。

1.333333	3	4	b	01-01-10-10	迭代次数n	4924	36409	40618.85	46367.03	53840.08
1.333333	3	4	b	01-10-01-10	迭代次数n	5079	36480	40784.88	45512.43	52834.54

同样的这两组也是相同的。

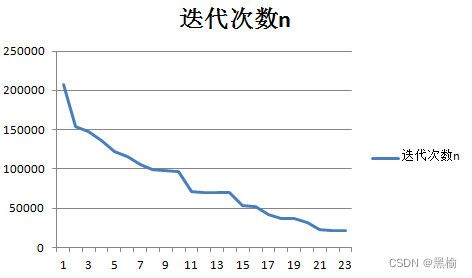
观察S平均和迭代次数n曲线，尽管个别数据有误差但总体上S和n之间的反比关系依然是清晰的。

因为S统计的是与训练集图片数量相关的平均值，因此可以将这次的数据和上次的一个训练集有2张图片另一个训练集里有1张图片的数据横向比较。

S平均	a	a	a	a	a	a	a	a	a	迭代次数n
0.333333	3	1	b	01-01-11-01	迭代次数n	13432.36	139891.7	157113.9	179519.3	207188.2
0.333333	3	1	b	01-11-11-11	迭代次数n	12676.79	107286.2	117513.9	133028.4	154503.1
0.666667	3	2	b	01-11-10-11	迭代次数n	15719.23	104694.3	114401.5	126914.8	147143.7
0.5	2	1	17	01*11*01	迭代次数n	9032.397	90425.22	101844	116066.1	135622.8
1	2	2	16	01*10*11	迭代次数n	13090.89	86782.35	95818.05	105586.1	122018.8
1	3	3	b	01-01-10-11	迭代次数n	12799.57	86593.53	94449.04	104090.8	116335.3
0.666667	3	2	b	01-10-10-10	迭代次数n	9729.462	71300.71	81367.92	92317.08	105625.9
0.5	2	1	19	01*11*11	迭代次数n	8406.095	69204.37	75918.46	87127.38	99695.94
0.5	2	1	19	10*11*11	迭代次数n	8452.266	69044.21	77609.65	85774.66	98321.27
0.666667	3	2	b	01-11-11-01	迭代次数n	6608.085	63333.77	71977.75	83191.75	96217.09
0.666667	3	2	b	01-01-11-11	迭代次数n	6267.251	49675.77	55069.35	62602.73	71207.15
1	2	2	14	01*10*01	迭代次数n	6562.407	49626.37	53976.52	62830.33	70601
0.666667	3	2	b	11-01-01-11	迭代次数n	6198.186	49881.95	55585.57	62915.46	70390.47
1	2	2	13	01*10*10	迭代次数n	6598.779	49677.57	55886.44	61773.39	69684.19
1.333333	3	4	b	01-01-10-10	迭代次数n	4923.854	36408.93	40618.85	46367.03	53840.08
1.333333	3	4	b	01-10-01-10	迭代次数n	5078.638	36479.74	40784.88	45512.43	52834.54
1	3	3	b	01-10-11-10	迭代次数n	4718.648	29763.91	33889.95	37498.31	42272.53
1	2	2	11	01*01*11	迭代次数n	4492.035	26777.36	29753.34	32949.8	37123.12
1	2	2	21	11*11*01	迭代次数n	4503.588	27240.86	29794.58	33117.16	36974.64
2	2	4	10	01*01*10	迭代次数n	3456.523	22841.7	25195.83	28372.41	31827.38
1.333333	3	4	b	01-11-11-10	迭代次数n	3028.879	15452.6	17931.25	19334.8	22579.88
1.5	2	3	18	01*11*10	迭代次数n	2946.296	16381.41	16983.82	19169.93	22057.13
1.666667	3	5	b	01-01-11-10	迭代次数n	3010.307	16673.54	17539.43	19642.51	21521.67

再次比较s和n的曲线，会发现这曲线S随着统计网络的增加变得平滑了很多。当然同样不可否认的是如果仅仅用S曲线去判断两个网络迭代次数的大小，个别情况确实会判断错误。

空间是有结构的，而移位距离值不足以表达空间结构的差异，比如(0,1)和(1,1)与(1,0)和(1,1)之间的移位距离都是1。但是01*01*11和01*10*11两个网络的迭代次数差异巨大

01*10*11	迭代次数n	13090.89	86782.35	95818.05	105586.1	122018.8
01*01*11	迭代次数n	4492.035	26777.36	29753.34	32949.8	37123.12

任意给定一个区间都可以确定在这一区间内有多少个自然数，并且可以按照大小精确的排序。如果任意给定3张图片，可能存在的空间形态差异也可以被精确的排序吗？