支持向量机（三）二分类SVC中样本不均衡问题+SVC模型的评估指标（混淆矩阵+ROC曲线相关问题）

1 二分类SVC中的样本不均衡问题：重要参数class_weight

分类模型天生会倾向于多数的类，让多数类更容易被判断正确，少数类被牺牲掉。因为对于模型而言，样本
量越大的标签可以学习的信息越多，算法就会更加依赖于从多数类中学到的信息来进行判断。如果我们希望捕获少数类，模型就会失败。其次，模型评估指标会失去意义。这种分类状况下，即便模型什么也不做，全把所有人都当成不会犯罪的人，准确率也能非常高，这使得模型评估指标accuracy变得毫无意义，根本无法达到我们的“要识别出会犯罪的人”的建模目的。

1.1 SVC的参数：class_weight

可输入字典或者"balanced”，可不填，默认None 对SVC，将类i的参数C设置为class_weight [i] 乘以 C。如果没有给出具体的class_weight，则所有类都被假设为占有相同的权重1，模型会根据数据原本的状况去训练。如果希望改善样本不均衡状况，请输入形如{“标签的值1”：权重1，“标签的值2”：权重2}的字典，则参数C将会自动被设为：标签的值1的C：权重1 * C，标签的值2的C：权重2*C.**

1.2 SVC的接口fit的参数：sample_weight

必须对应输入fit中的特征矩阵的每个样本每个样本在fit时的权重，让权重乘以每个样本对应的C值来迫使分类器强调设定的权重更大的样本。通常，较大的权重加在少数类的样本上，以迫使模型向着少数类的方向建模

通常来说，class_weight和sample_weight这两个参数我们只选取一个来设置。如果我们同时设置了两个参数，则C会同时受到两个参数的影响，即 class_weight中设定的权重 乘以 sample_weight中设定的权重 *C。

from sklearn.svm import SVC
from sklearn.datasets import make_blobs
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import confusion_matrix as CM, precision_score as P, recall_score as R


class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)
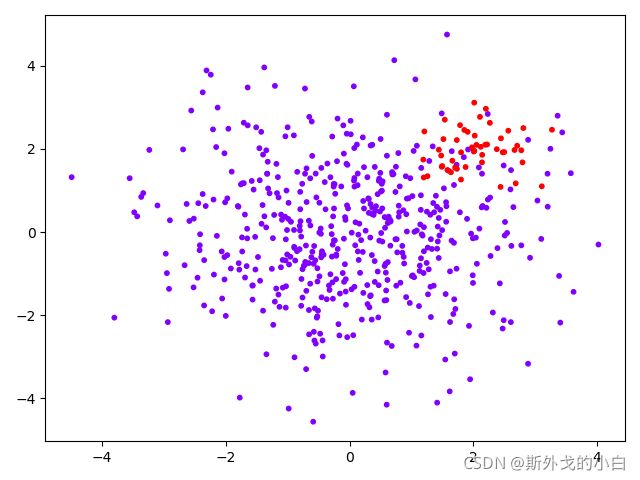
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow",s=10)
#其中红色点是少数类，紫色点是多数类

#不设定class_weight
clf = SVC(kernel='linear', C=1.0)
clf.fit(X, y)

#设定class_weight
wclf = SVC(kernel='linear', class_weight={1: 10})
wclf.fit(X, y)

#给两个模型分别打分看看，这个分数是accuracy准确度
print(clf.score(X, y)) #0.9418181818181818
print(wclf.score(X, y)) #0.9127272727272727

可以看出不带权重的准确率更高，是不是可以认为不权重的预测是更好的预测？

#首先要有数据分布
plt.figure(figsize=(6, 5))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="rainbow", s=10)
ax = plt.gca()

#获取当前的子图，如果不存在，则创建新的子图
#绘制决策边界的第一步：要有网格
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T


#第二步：找出我们的样本点到决策边界的距离
Z_clf = clf.decision_function(xy).reshape(XX.shape)
a = ax.contour(XX, YY, Z_clf, colors='black', levels=[0], alpha=0.5, linestyles=['-'])

Z_wclf = wclf.decision_function(xy).reshape(XX.shape)
b = ax.contour(XX, YY, Z_wclf, colors='red', levels=[0], alpha=0.5, linestyles=['-'])

#第三步：画图例
plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
           loc="upper right")
plt.show()

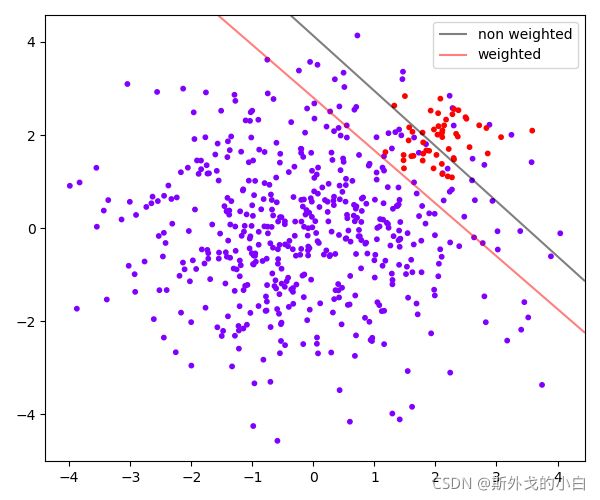
从准确率的角度来看，不做样本平衡的时候准确率反而更高，做了样本平衡准确率反而变低了，这是因为做了样本平衡后，为了要更有效地捕捉出少数类，模型误伤了许多多数类样本，而多数类被分错的样本数量 > 少数类被分类正确的样本数量，使得模型整体的精确性下降。现在，如果我们的目的是模型整体的准确率，那我们就要拒绝样本平衡，使用class_weight被设置之前的模型。

2 SVC的模型评估指标

2.1 混淆矩阵confusion matrix

混淆矩阵是二分类问题的多维衡量指标体系，在样本不平衡时极其有用。在混淆矩阵中，我们将少数类认为是正例，多数类认为是负例。

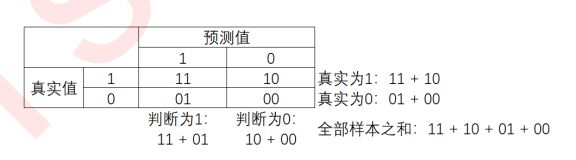
可以很容易看出，11和00的对角线就是全部预测正确的，01和10的对角线就是全部预测错误的。基于混淆矩阵，我们有六个不同的模型评估指标，这些评估指标的范围都在[0,1]之间，所有以11和00为分子的指标都是越接近1越好，所以以01和10为分子的指标都是越接近0越好。对于所有的指标，我们用橙色表示分母，用绿色表示分子，则我们有：

2.1.1 模型的整体效果：准确率

准确率Accuracy就是所有预测正确的所有样本除以总样本，通常来说越接近1越好。

2.1.2 捕捉少数类的艺术：Precision和Recall、F1 score

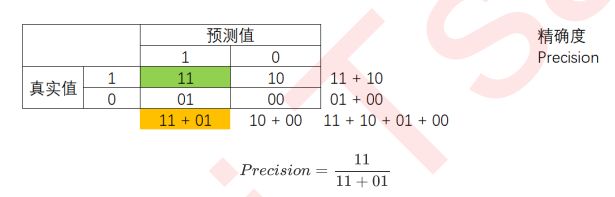
精确度Precision，又叫查准率，表示所有被我们预测为是少数类的样本中，真正的少数类所占的比例。精确度是”将多数类判错后所需付出成本“的衡量。

#精确度precision计算
precision_1 = (y[y == clf.predict(X)] == 1).sum() / (clf.predict(X) == 1).sum()
precision_2 = (y[y == wclf.predict(X)] == 1).sum() / (wclf.predict(X) == 1).sum()

print(precision_1, precision_2)
#0.7142857142857143
#0.5102040816326531
#我们可以看出，经过样本平衡之后的精确率下降了，所以当我们将多数类判断错误的成本非常高昂的时候，就要求较高的精确度

可以看出，做了样本平衡之后，精确度是下降的。因为很明显，样本平衡之后，有更多的多数类紫色点被我们误伤了。精确度可以帮助我们判断，是否每一次对少数类的预测都精确，所以又被称为”查准率“。在现实的样本不平衡例子中，当每一次将多数类判断错误的成本非常高昂的时候（比如大众召回车辆的例子），我们会追求高精确度。精确度越低，我们对多数类的判断就会越错误。当然了，如果我们的目标是不计一切代价捕获少数类，那我们并不在意精确度。

召回率Recall，又被称为敏感度(sensitivity)，真正率，查全率，表示所有真实为1的样本中，被我们预测正确的样本所占的比例。

#召回率recall计算
recall_1 = (y[y == clf.predict(X)] == 1).sum() / (y == 1).sum()
recall_2 = (y[y == wclf.predict(X)] == 1).sum() / (y ==1).sum()

print(recall_1, recall_2)
#0.6 , 1

可以看出，做样本平衡之前，我们只成功捕获了60%左右的少数类点，而做了样本平衡之后的模型，捕捉出了
100%的少数类点，从图像上来看，我们的红色决策边界的确捕捉出了全部的少数类，而灰色决策边界只捕捉到了一半左右。召回率可以帮助我们判断，我们是否捕捉除了全部的少数类，所以又叫做查全率。

如果我们希望不计一切代价，找出少数类（比如找出潜在犯罪者的例子），那我们就会追求高召回率，相反如果我们的目标不是尽量捕获少数类，那我们就不需要在意召回率。

而召回率和精确度是此消彼长的，两者之间的平
衡代表了捕捉少数类的需求和尽量不要误伤多数类的需求的平衡。究竟要偏向于哪一方，取决于我们的业务需求：究竟是误伤多数类的成本更高，还是无法捕捉少数类的代价更高。

为了同时兼顾精确度和召回率，我们创造了两者的调和平均数作为考量两者平衡的综合性指标，称之为F1
measure。两个数之间的调和平均倾向于靠近两个数中比较小的那一个数，因此我们追求尽量高的F1
measure，能够保证我们的精确度和召回率都比较高。F1 measure在[0,1]之间分布，越接近1越好。

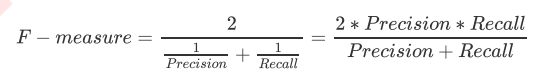
从Recall延申出来的另一个评估指标叫做假负率（False Negative Rate），它等于 1 - Recall，用于衡量所有真实为1的样本中，被我们错误判断为0的，通常用得不多。

2.1.3判错多数类的考量：特异度与假正率

#特异度specificity
spe_1 = (y[y == clf.predict(X)] == 0).sum() / (y == 0).sum()
spe_2 = (y[y == wclf.predict(X)] == 0).sum() / (y == 0).sum()
print(spe_1, spe_2)
#0.976   0.904

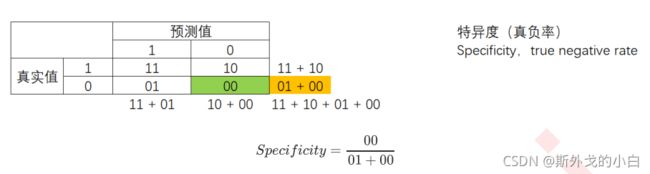
特异度衡量了一个模型将多数类判断正确的能力，而1 - specificity就是一个模型将多数类判断错误的能力，这种
能力被计算如下，并叫做假正率（False Positive Rate）：

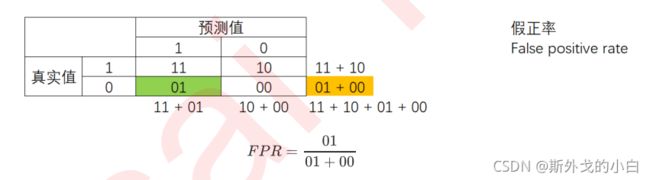
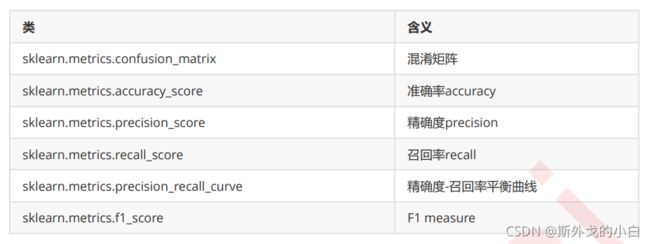
2.1.4 sklearn中的混淆矩阵

2.2 ROC曲线相关问题

假正率有一个非常重要的应用：我们在追求较高的Recall的时候，Precision会下降，就是说随着更多的少数类被捕捉出来，会有更多的多数类被判断错误，但我们很好奇，随着Recall的逐渐增加，模型将多数类判断错误的能力如何变化呢？

每判断正确一个少数类，就有多少个多数类会被判断错误。假正率正好可以帮助我们衡量这个能力的变化。我们可以使用Recall和FPR之间的平衡，来替代Recall和Precision之间的平衡，让我们衡量模型在尽量捕捉少数类的时候，误伤多数类的情况如何变化，这就是我们的ROC曲线衡量的平衡。

2.2.1 概率和阈值

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

class_1 = 7
class_2 = 4
centers = [[0.0, 0.0], [1, 1]]
cluster_std = [0.5, 1]
x, y = make_blobs(n_samples=[class_1, class_2],
                 centers = centers,
                 cluster_std = cluster_std,
                 random_state = 0,
                 shuffle = False)
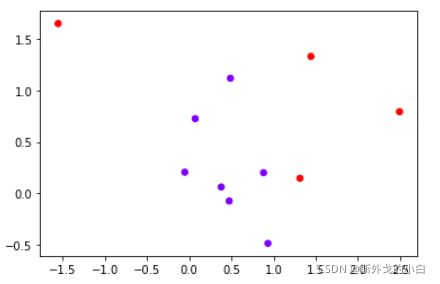
plt.scatter(x[:, 0], x[:,1], c=y, cmap="rainbow", s=30)

建模，调用概率

from sklearn.linear_model import LogisticRegression as logiR
clf_lo = logiR().fit(x, y)
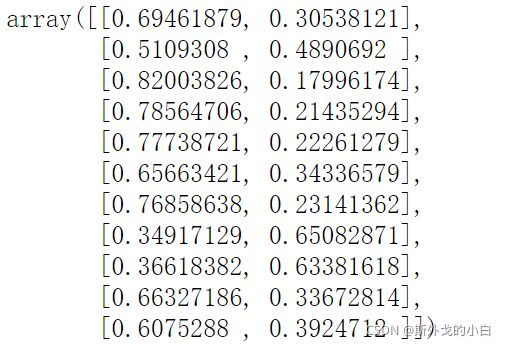
prob = clf_lo.predict_proba(x)
prob

import pandas as pd

prob = pd.DataFrame(prob)
prob.columns = ["0", "1"]

prob

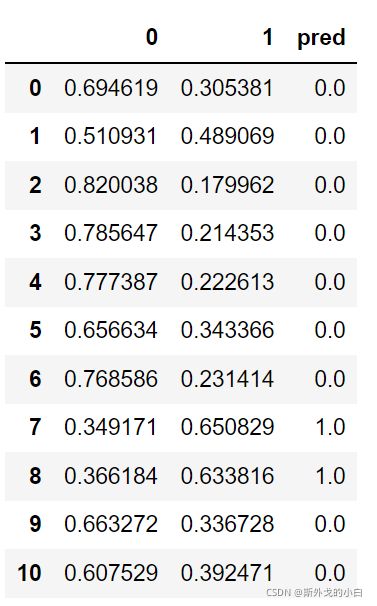
for i in range(prob.shape[0]):
    if prob.loc[i,"1"] > 0.5:
        prob.loc[i, "pred"] = 1
    else:
        prob.loc[i, "pred"] = 0

prob

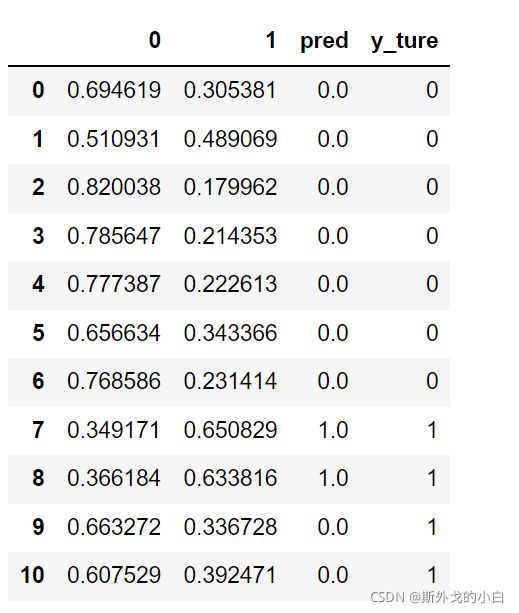
prob["y_ture"] = y

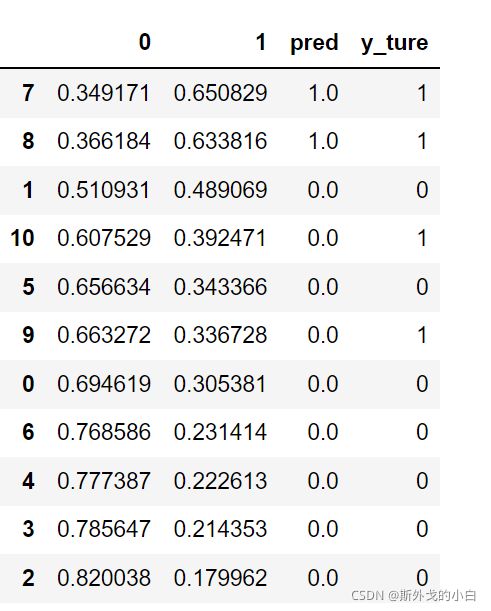
prob = prob.sort_values(by="1", ascending=False)
prob

使用混淆矩阵查看结果

from sklearn.metrics import confusion_matrix as CM, precision_score as P, recall_score
as R

CM(prob.loc[:, "y_ture"], prob.loc[:, "pred"], labels=[1, 0])

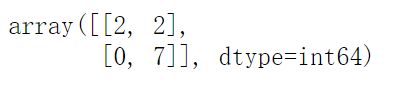
同时按下shift和tab键可以看到cm的参数如何分布，首先输入真实值，其次输入预测值，再给出少数分布和多数分布的标签值，在这里我们的少数分布标签为1

P(prob.loc[:, "y_ture"], prob.loc[:, "pred"], labels=[1, 0])
#1
R(prob.loc[:, "y_ture"], prob.loc[:, "pred"], labels=[1, 0])
#0.5

刚才我们设置的阈值为0.5，现在调整阈值为0.4，再看一下结果如何

for i in range(prob.shape[0]):
    if prob.loc[i,"1"] > 0.4:
        prob.loc[i, "pred"] = 1
    else:
        prob.loc[i, "pred"] = 0
prob_ = prob.sort_values(by="1", ascending=False)
prob_

CM(prob_.loc[:, "y_ture"], prob_.loc[:, "pred"], labels=[1, 0])

P(prob_.loc[:, "y_ture"], prob_.loc[:, "pred"], labels=[1, 0])
#0.6666666666666666
R(prob.loc[:, "y_ture"], prob.loc[:, "pred"], labels=[1, 0])
#0.5

但是注意，并不是升高阈值，就一定能够增加或者减少Recall，一切要根据数据的实际分布来进行判断。

2.2.2 SVM实现概率预测

重要参数probability，接口predict_proba以及
decision_function

接口decision_function返回的值也因此被我们认为是SVM中的置信度（confidence）。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_blobs

class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)
clf_proba = SVC(kernel="linear", C=1.0, probability=True).fit(X, y)
print(clf_proba.predict_proba(X)) #二分类问题只有两列值
print(clf_proba.predict_proba(X).shape) #(550, 2)
print(clf_proba.decision_function(X))

2.2.3 绘制ROC曲线

from sklearn.svm import SVC
from sklearn.datasets import make_blobs
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import confusion_matrix as CM, precision_score as P, recall_score as R


class_1 = 500 #类别1有500个样本
class_2 = 50 #类别2只有50个
centers = [[0.0, 0.0], [2.0, 2.0]] #设定两个类别的中心
clusters_std = [1.5, 0.5] #设定两个类别的方差，通常来说，样本量比较大的类别会更加松散
X, y = make_blobs(n_samples=[class_1, class_2],
                  centers=centers,
                  cluster_std=clusters_std,
                  random_state=0, shuffle=False)

clf = SVC(kernel="linear", C=1, probability=True).fit(X, y)

prob = clf.predict_proba(X)
#print(clf.predict_proba(X))
#print(clf.predict_proba(X).shape) #(550, 2)
#print(clf.decision_function(X))

prob = pd.DataFrame(prob)
#print(prob)

#print(prob.loc[:, 1])
probrange = np.linspace(prob.loc[:, 1].min(), prob.loc[:, 1].max(), num=50, endpoint=False)
#print(probrange)
#endpoint=False的意思是不取最大值，因为linspace是左闭右闭区间

recall = []
FPR = []
for i in probrange:
    y_predict = []
    for j in range(prob.shape[0]):
        if prob.loc[j, 1] > i:
            y_predict.append(1)
        else:
            y_predict.append(0)
    cm = CM(y, y_predict, labels=[1, 0])
    recall.append(cm[0, 0]/cm[0, :].sum())
    FPR.append(cm[1, 0]/cm[1, :].sum())

recall.sort()
FPR.sort()

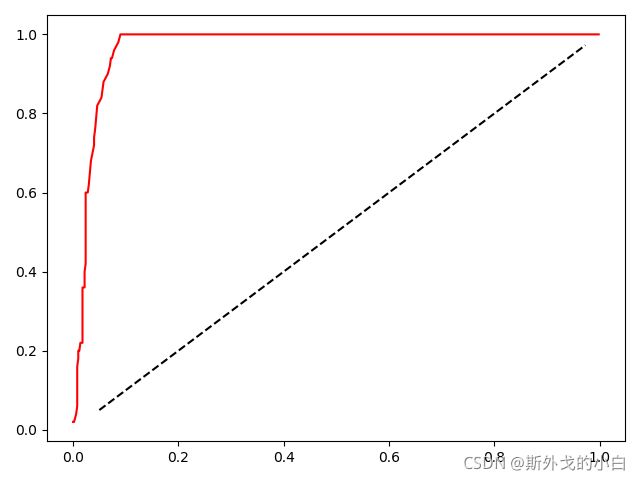
plt.plot(FPR, recall, c="red")
plt.plot(probrange+0.05, probrange+0.05, c="black", linestyle="--")
plt.show()

可以直接调用sklearn中的接口来绘制ROC曲线

from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score as AUC

FPR, recall, thresholds = roc_curve(y, clf.decision_function(X), pos_label=1)
print(FPR, recall, thresholds)

#我们这里的阈值之所以会超过0-1的范畴是因为以每个点到决策边界的距离为计算标准的
area = AUC(y, clf.decision_function(X))
print(area)
#0.9696400000000001

recall_FPR_gap = (recall - FPR).tolist()
max_gap = max(recall_FPR_gap)
#print(max_gap)  #0.914

max_index = recall_FPR_gap.index(max_gap)
#print(max_index) #43

#print(thresholds[max_index]) #-1.0860191749391461

recall_FPR_gap = (recall - FPR).tolist()
max_gap = max(recall_FPR_gap)
#print(max_gap)  #0.914

max_index = recall_FPR_gap.index(max_gap)
#print(max_index) #43

#print(thresholds[max_index]) #-1.0860191749391461

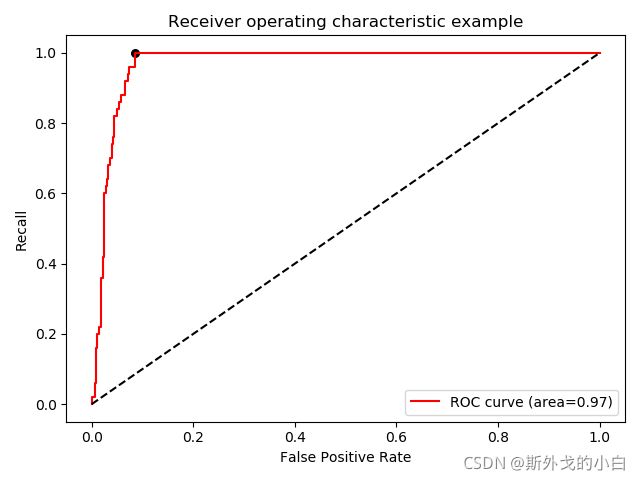
plt.figure()
plt.scatter(FPR[max_index], recall[max_index], c="black", s=30)
plt.plot(FPR, recall, color="red", label="ROC curve (area=%.2f)" % area)
plt.plot([0, 1], [0, 1], color="black", linestyle="--")
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel("False Positive Rate")
plt.ylabel("Recall")
plt.title("Receiver operating characteristic example")
plt.legend(loc="lower right")
plt.show()

其他内容为选读内容——针对多分类问题，如何使用SCV