手动计算ROC-AUC_fFr9w5rHXUMG7V9szVcusW
手动计算ROC-AUC
ROC(全称为Receiver operating characteristic,意为受试者特征曲线)是一个二维平面空间中一条曲线,而AUC则是曲线下方面积(Area Under Curve)的计算结果,是一个具体的值
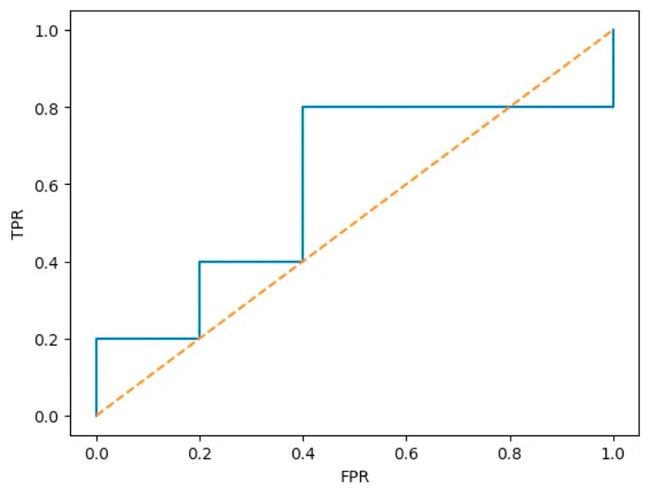
x轴是FPR,y轴是TPR,曲线上的每个点就对应着一组(FPR,TPR)坐标,所以我们的任务就是计算出所有的(FPR,TPR)坐标然后用线把他们连接起来就形成了ROC曲线,而AUC可以通过曲线下面积计算而来。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import RocCurveDisplay
首先手动创建一组预测值和对应的真实值,0一般为负类,1为正类,而且正类多设置为研究中较为关心的标签,比如把1设置为肿瘤,或者疾病。
np.random.seed(1314)
geneA = np.random.uniform(size=10)
label = [0]*5 + [1]*5
df = pd.DataFrame({'geneA':geneA,'label':label})
df = df.sort_values('geneA',ascending=False)
df.reset_index(drop=True,inplace=True) # 恢复行索引从0开始递增
df
geneA label
0 0.928483 1
1 0.864400 0
2 0.828642 1
3 0.749421 0
4 0.464414 1
5 0.407268 1
6 0.210935 0
7 0.140796 0
8 0.082719 0
9 0.012973 1
从1开始降低阈值,当geneA小于阈值时被预测为0类,当geneA大于阈值时被预测为1类;
当阈值为1时,所有样本被预测为0类,则可以算得FPR=FP/AN;TPR= TP/AP
-
FP:(假阳性)真实为0类,但是却被预测为1类的样本个数;
-
AN:(真阴性)真实为0类的样本个数;
-
TP:(真阳性)真实为1类,被预测为1类的样本个数;
-
AP:(真阳性)真实为1类的样本个数;
此时FPR=0/5=0; FPR=0/5=0。因此,可以得到第一个坐标(0,0)
降低阈值,当阈值=0.9时, 第0条数据被预测为1类,而且其真实标签也为1;此时FPR=0/5=0; TPR=1/5=0。因此,可以得到第一个坐标(0,0.2)
降低阈值,当阈值=0.8时,第0、2条数据真实标签为0,但是却被预测为1;第2、3、5条数据真实标签为1,也被预测为1,因此,此时FPR=1/5=0.2; TPR=2/5=0.4。因此,可以得到下一个坐标(0.2,0.4)
# 定义ROC曲线绘制函数
def plot_ROC(y_true, y_pred, threds, title='ROC_curve'):
"""
ROC绘制曲线函数:
:param y_true: 样本真实类别
:param y_pred: 模型输出的类别概率判别结果
:param threds: 阈值1Darray
:param title: 折线图的图例
:return: no return
"""
TPR_l = []
FPR_l = []
for i in threds:
y_cla = np.array(y_pred>i,dtype=int) # True 转变成1, False = 0
Positive = y_cla[y_true > 0.5]
TPR_l.append(Positive.mean())
Negtive = y_cla[y_true < 0.5]
FPR_l.append(Negtive.mean())
plt.plot(FPR_l, TPR_l, label=title)
plt.plot([0,1], [0,1], '--')
plt.xlabel('FPR')
plt.ylabel('TPR')
# p = plt.gcf()
# p.set_size_inches(4, 4)
为了模仿sklearn中的ROC图,这里的阈值列表设置为[0,1]之间随机取1000个数,可以看到图形和sklearn的一模一样。
plot_ROC(y_true=np.array(label),y_pred=geneA,
threds=np.linspace(0,1,1000,endpoint=True))
# sklearn 绘图
RocCurveDisplay.from_predictions(label,geneA)
plt.plot([0,1], [0,1], '--');
计算AUC,AUC的定义是曲线下面积,按道理可以计算面积就行,但是如果样本较多,则会变成一条近似的曲线,计算了太大,因此有更好的方法计算AUC,比如
A U C = ∑ 样本 i ∈ 正样本 r i − P ∗ ( P + 1 ) 2 P ∗ N A U C=\frac{\sum_{\text {样本}_i \in \text { 正样本 }} r_{i}-\frac{P *(P+1)}{2}}{P * N} AUC=P∗N∑样本i∈ 正样本 ri−2P∗(P+1)
-
P:正样本个数,1类;
-
N:负样本个数,0类;
-
ri: 正样本的排序号,下边dataframe中rank那一列
df = df.sort_values('geneA',ascending=True)
df.reset_index(drop=True,inplace=True) # 恢复行索引从0开始递增
df['Rank'] = df.index + 1 # 新增加一列是geneA排序大小
df
geneA label Rank
0 0.012973 1 1
1 0.082719 0 2
2 0.140796 0 3
3 0.210935 0 4
4 0.407268 1 5
5 0.464414 1 6
6 0.749421 0 7
7 0.828642 1 8
8 0.864400 0 9
9 0.928483 1 10
按照公式分别计算,得到AUC为0.6,下边我们把auc计算写成一个函数
P = 5; N =5; PP = P*(P+1)/2
((1+5+6+8+10) - PP) / (P * N)
def auc(y_true, y_pred):
df = pd.DataFrame({'y_true':y_true,'y_pred':y_pred})
df = df.sort_values('y_pred',ascending=True)
df.reset_index(drop=True,inplace=True) # 恢复行索引从0开始递增
df['Rank'] = df.index + 1 # 新增加一列是geneA排序大小
P = np.nansum(df.y_true > 0.5)
N = df.shape[0] - P
PP = P*(P+1)/2
r = map(lambda x: np.mean(df.Rank[df.y_pred == df.y_pred[x]]), df.index[df.y_true == 1])
AUC = (np.nansum(list(r))-PP)/(P*N)
return AUC
map这样写是因为,如果有一个1类的y_pred数值(本例中geneA)和另一个0类的geneA数值相同的话,需要计算他们两个的Rank数值的均值
map(lambda x: np.mean(df.Rank[df.y_pred == df.y_pred[x]]), df.index[df.y_true == 1])