机器学习笔记3：分类

目录

1.数据集准备

2. 评价指标

2.1 混淆矩阵

2.2 精度和召回率

2.3 F1分数

2.4 精度/召回率权衡

2.5 绘制ROC曲线

2.6 曲线下面积（AUC） 

3. 模型对比

4. 多类分类器

5. 误差分析

---

1.数据集准备

本文采用MNIST数据集，这是一组由美国高中生和人口调查局员工手写的7w个数字的图片，每张图片都有对应的目标值，该数据集应用非常广泛。

from sklearn.datasets import fetch_openml
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

mnist = fetch_openml('mnist_784', version=1, as_frame=False)
mnist.keys()

## dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])

该数据集已经在sklearn库里，直接调用即可，这里只使用他的data（特征值）和target（目标值）

X, y = mnist["data"], mnist["target"]
X.shape

## (70000, 784)

y.shape

## (70000, 1)

 可以看出特征值由784个特征，也就是28*28像素

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off")
plt.show()

y[0]

## '5'

将第一个样本特征值可视化得到该图，与目标值同为5（只不过目标值是字符串形式

y = y.astype('int32')
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

将目标值都改为整数形，并且区分开训练集和测试集，该数据集已经分好前6w条是训练集

# 二元判断器
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)

由浅入深，先构建模型判断一个数字是不是5

# 训练一个SGD模型
from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
sgd_clf.fit(X_train, y_train_5)

构造一个随机梯度下降（SGD）分类器，参数的意义先不用管

# 交叉验证准确率
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

## array([0.95035, 0.96035, 0.9604 ])

准确率看着还行但其实意义不大，哪怕你写一个判断函数判定所有数字都不是5，准确率都有90%。所以准确率这项指标并不是很靠谱，后面会介绍更多指标

2. 评价指标

2.1 混淆矩阵

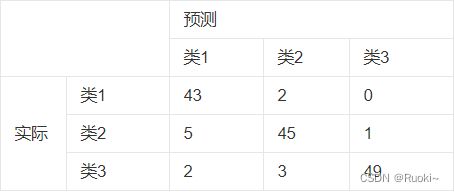
混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目：第一行第一列中的43表示有43个实际归属第一类的实例被预测为第一类，同理，第一行第二列的2表示有2个实际归属为第一类的实例被错误预测为第二类。

 要计算混淆矩阵就必须要有一组预测值与目标值进行比较，预测集是留在项目的最后才使用，我们这里先用croos_vak_predict()函数进行替代，croos_vak_predict函数是执行K折交叉验证，但返回的是每个折叠的预测值，这意味着每个实例都可以会在没有经过该实例训练出的模型上进行预测。

# 每个折叠的预测
# 在不动测试集的前提下，这样能用模型预测训练集
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
y_train_pred

利用confusion_matrix()函数得到混淆矩阵

# 混淆矩阵
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)

array([[53892,   687],
       [ 1891,  3530]])

53892=预测为非5且实际为非5（真负类），1891=预测为非5但实际为5（假正类）

687=预测为5且实际为非5（假负类），3530=预测为5且实际为5（真正类）

import scikitplot as skplt
# 混淆矩阵
plot = skplt.metrics.plot_confusion_matrix(y_train_5, y_train_pred)
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.xlabel('真实类别')
plt.ylabel('预测类别')
plt.title('')
plt.show()

混淆矩阵可视化

2.2 精度和召回率

混淆矩阵能提供大量信息，但有时你希望指标更简洁一些，正类预测的准确率是一个不错的指标，它也被称为精度

精度=(TP) / (TP+FP)

它通常搭配着召回率一起使用

召回率=(TP) / (TP+FN)

从公式不难看出两种指标的意义，精度是指抓的准、召回率是指抓的全。这两个指标也是不可兼得的（通常），你可以搭配logic模型进行理解，随着你阈值的增大，精度会增加召回率会减小。阈值降低则反之。不同的运用场景对两种指标的要求也不同，比如一个审核不良视频的模型，你可能想要一个拦截了很多好视频（精度低），但是剩下的视频都是安全的（召回率高）。在指纹解锁大门的模型中，你会想要自己有时候都打不开（召回率低），但别人一定打不开的大门（精度高），两种指标的取舍因情况而定。

 代码实现：

from sklearn.metrics import precision_score, recall_score
print('精度：',precision_score(y_train_5, y_train_pred))
print('召回率：',recall_score(y_train_5, y_train_pred))

##精度： 0.8370879772350012
##召回率： 0.6511713705958311

当模型说一个数字是5时，83%的概率真的是5。并且只有65%的5被识别为5，有很大的进步空间。一个判定所有数字都不是5的模型，那他的精度和召回率都是0。一个判定所有数字都是5的模型，那他的精度是10%（假设每个数字的个数相同），召回率是100%

2.3 F1分数

如果你对精度和召回率的重视程度差不多的话，你可以简单把他们组合一下，成为F1分数。当你需要一个简单的办法比较两种分类器时，这是个非常不错的指标

F1=2 × (精度×召回率) / (精度+召回率)

from sklearn.metrics import f1_score
print('F1分数：',f1_score(y_train_5, y_train_pred))

## F1分数： 0.7325171197343846

2.4 精度/召回率权衡

来看看SGDclassifier是如何进行分类决策的，对于每个样本，他会根据决策函数计算出一个分值，如果该值大于阈值，则判定为正类，否则判定为负类。

在Scikit-Learn不允许直接设置阈值，但是可以利用decision_function()方法得到每个样本的决策分数，然后根据自己设置的阈值进行判断

（有些机器模型例如随机森林没有该方法，那就使用dict_proba()方法，该方法返回的是一个数组，其中每行代表一个实例，每列代表一个类别，意思是该实例属于某个类别的概率。）

y_scores2 = sgd_clf.decision_function([X_train[-1]])
print('决策分数:',y_scores2)
threshold = 0
y_some_digit_pred=(y_scores2>threshold)
y_some_digit_pred
## 决策分数:-3991.49590678
## array([True])

你也可以一开始训练模型的时候就利用cross_val_predict()函数返回所有实例的分数而不是预测结果（前面方法是得到单一的决策分数，该方法是得到全部的分数，且所有模型都能使用）

# 返回每个实例的分数
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")

再获取所有可能的阈值和对应的精度、召回率

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
# 精度、召回率、阈值

然后再美美画个图，你可以找出精度>90%的第一个阈值

# 可视化方法1
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.legend(loc="center right", fontsize=16) # Not shown in the book
    plt.xlabel("Threshold", fontsize=16)        # Not shown
    plt.grid(True)                              # Not shown
    plt.axis([-50000, 50000, 0, 1])             # Not shown


# 找到精度>90的第一个点
recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]


plt.figure(figsize=(8, 4))                                                                  # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")                 # Not shown
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")                                # Not shown
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")# Not shown
plt.plot([threshold_90_precision], [0.9], "ro")                                             # Not shown
plt.plot([threshold_90_precision], [recall_90_precision], "ro")                             # Not shown
#save_fig("precision_recall_vs_threshold_plot")                                              # Not shown
plt.show()

这里你也会发现并不是阈值提高精度一定提高的，所以希望你注意到了前面括号里的“通常”

你也可以画出精度和召回率的对比图

# 可视化方法2
def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
plt.show()

当你选好了阈值，你可以直接计算对应的精度和召回率

# 精度为90时的召回率
y_train_pred_90 = (y_scores >= threshold_90_precision)
print("精度",precision_score(y_train_5, y_train_pred_90))
print('召回率',recall_score(y_train_5, y_train_pred_90))

## 精度 0.9000345901072293
## 召回率 0.4799852425751706

2.5 绘制ROC曲线

ROC曲线绘制的是真正类率（召回率）和假正类率（FPR），假正类率是错误分到正类的负类比例，它等于1-真负类率（TNR），TNR也称特异度，所以ROC曲线绘制的是灵敏度（召回率）和（1-特异度）的关系

绘制时使用roc_curve（）函数计算多种TPR和FPR

# 计算多组FPR和TPR
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

# 绘制ROC曲线
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
    plt.axis([0, 1, 0, 1])                                    # Not shown in the book
    plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # Not shown
    plt.ylabel('True Positive Rate (Recall)', fontsize=16)    # Not shown
    plt.grid(True)                                            # Not shown

plt.figure(figsize=(8, 6))                                    # Not shown
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)]           # Not shown
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")   # Not shown
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")  # Not shown
plt.plot([fpr_90], [recall_90_precision], "ro")               # Not shown                                 # Not shown
plt.show()
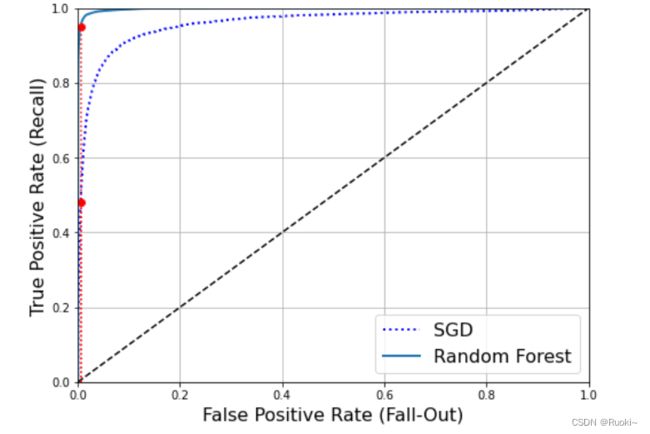
# 红色标记为选定的召回率（精度90对应的

同样从图像也能看出，真正类率越大，假正类率也越大，虚线表示的是纯随机分类器的ROC曲线，一个优秀的分类器应该离这条线越远越好

PS:ROC曲线和PR曲线非常相似，有一个经验法则是，当正类非常少见或者你更关注假正类而不是假负类时，应该选择PR曲线，反之则是ROC曲线。例如，看前面的ROC曲线以及后面的AUC分数你会觉得分类器真不错，但主要是因为跟负类相比正类真的太少，相比之下PR曲线清楚说明分类器还有改进的空间（曲线可以更接近左上角）

2.6 曲线下面积（AUC） 

AUC就是ROC曲线与X轴围成的面积，完美的分类器AUC应该等于1，纯随机的分类器AUC应该等于0.5。

# AUC分数
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)

## 0.9604938554008616

3. 模型对比

建立一个随机森林模型进行对比

# 训练个随机森林模型做对比
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=100, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
# 第一列是负类概率，第二列是正类概率
y_probas_forest

array([[0.11, 0.89],
       [0.99, 0.01],
       [0.96, 0.04],
       ...,
       [0.02, 0.98],
       [0.92, 0.08],
       [0.94, 0.06]])

得到多组TPR和FPR的值
y_scores_forest = y_probas_forest[:, 1] # 分数=正类的概率
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)

# 对比ROC曲线
recall_for_forest = tpr_forest[np.argmax(fpr_forest >= fpr_90)]

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")
plt.plot([fpr_90], [recall_90_precision], "ro")
plt.plot([fpr_90, fpr_90], [0., recall_for_forest], "r:")
plt.plot([fpr_90], [recall_for_forest], "ro")
plt.grid(True)
plt.legend(loc="lower right", fontsize=16)
plt.show()

# 随机森林的auc、精度、召回率
print('auc',roc_auc_score(y_train_5, y_scores_forest))
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
print('精度',precision_score(y_train_5, y_train_pred_forest))
print('召回率',recall_score(y_train_5, y_train_pred_forest))

##auc 0.9983436731328145
##精度 0.9905083315756169
##召回率 0.8662608374838591

4. 多类分类器

顾名思义，二元分类器是在两个类区分，多类分类器是在多个类进行区分。

有些分类器例如随机森林是直接处理多个类，也有一些严格的二元分类器例SVM是训练多个二元分类器。

• OvR

要训练一个模型将数字图片分为10类（0到9），一种方法是训练10个二元分类器，每个数字一个（0-检测器、1-检测器、...），当你需要对一张图片进行识别时，获取每个检测器的对应的分数，然后最后看哪个类分数最高。这称为一对多策略

• OvO

另一种方法是对每一对数字训练一个二元分类器，0-1分类器，0-2分类器、1-2分类器...这称为一对一策略

具体选择哪种策略要结合具体算法，比如支持向量机在数据规模扩大时表现糟糕，因此选择OvO策略（sklearn中支持向量机自动运行OvO策略），因为在较小训练集上分别训练多个分类器比在大型数据集上训练少数分类器要快得多。但对于大多数分类器OvR策略更好一些。

在Scikit-Learn中会根据情况自动选择OvO或者OvR，以上内容了解下就好了

• SVC分类器

# 默认使用OvO策略
from sklearn.svm import SVC

svm_clf = SVC(gamma="auto", random_state=42)
svm_clf.fit(X_train[:1000], y_train[:1000]) # y_train, not y_train_5
svm_clf.predict([some_digit])

## array([5])

# 强制使用OvR策略
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier

svm_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))
svm_clf.fit(X_train[:1000], y_train[:1000]) # y_train, not y_train_5
svm_clf.predict([some_digit])

## array([5])

# 查看各类分数
some_digit_scores = svm_clf.decision_function([some_digit])
print('各类分数：\n',some_digit_scores)
print('最大值的索引：',np.argmax(some_digit_scores))
# 一定要做这个，不是每次都刚好一一对应
print('每个索引对应的类别:',svm_clf.classes_)
print('svm预测该样本的类别：',svm_clf.classes_[5])

各类分数：
 [[ 2.81585438  7.09167958  3.82972099  0.79365551  5.8885703   9.29718395
   1.79862509  8.10392157 -0.228207    4.83753243]]
最大值的索引： 5
每个索引对应的类别: [0 1 2 3 4 5 6 7 8 9]
svm预测该样本的类别： 5

• SGD分类器

# 使用SGD分类器
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
## array([3])

# 对每一类的分数
sgd_clf.decision_function([some_digit])

array([[-31893.03095419, -34419.69069632,  -9530.63950739,
          1823.73154031, -22320.14822878,  -1385.80478895,
        -26188.91070951, -16147.51323997,  -4604.35491274,
        -12050.767298  ]])

将特征进行简单缩放，然后看看交叉验证的准确率

# 将特征值标准化后，再交叉验证看看
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")

## array([0.8983, 0.891 , 0.9018])

5. 误差分析

假设现在已经找到一个有潜力的模型，我们希望找到一些方法对其进行改进，方法之一就是分析其错误类型。

首先可以看下混淆矩阵

## 查看混淆矩阵
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
# 计算数字
conf_mx = confusion_matrix(y_train, y_train_pred)

# 可视化
#name = ['1', '2', '3', '4', '5','6','7','8','9']
figure = plt.figure()
axes = figure.add_subplot(111)

caxes=axes.matshow(conf_mx, interpolation ='nearest')
figure.colorbar(caxes)

#axes.set_xticklabels(['']+name)
#axes.set_yticklabels(['']+name)
plt.show()

  每行代表实际类，每列代表预测类。大多数图片都在主对角线上，说明他们都被正确分类，其中5数字暗一点，有可能是数据集中数字5的样本太少，也有可能是分类器在5上的效果并不好。

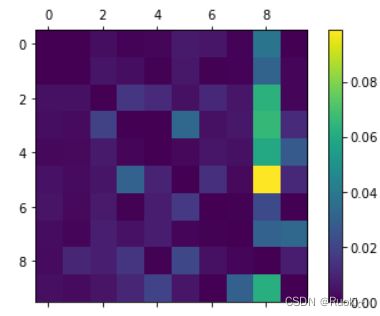
为了把焦点放在错误上，我们将混淆矩阵中每个值出意相应类中的图片数量，这样比较的就是错误率而不是错误的数量，这样对样本较少的数字公平。且大多数图片都在主对角线上，所以错误不明显，为了聚焦错误，将对角线全部填充为0，然后重新绘制。

# 图形显示错误率
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
figure = plt.figure()
axes = figure.add_subplot(111)
caxes=axes.matshow(norm_conf_mx, interpolation ='nearest')
figure.colorbar(caxes)
plt.show()

我们可以发现第8列很亮，说明很多数字都被错误的判为8，这样我们就可以把精力放在改进数字8分类错误的问题上了。