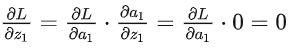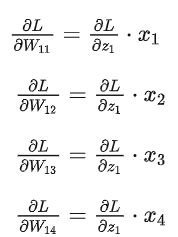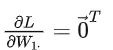NNDL 作业4:第四章课后题
目录
习题4-2 试设计一个前馈神经网络来解决XOR问题,要求该前馈神经网络具有两个隐藏神经元和一个输出神经元,并使用ReLU作为激活函数
习题4-5 试举例说明死亡ReLU问题,并给出解决方法。
习题4-7 为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化?
习题4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令W=0,b=0?
习题4-9 梯度消失问题是否可以通过增加学习率来缓解?
总结
习题4-2 试设计一个前馈神经网络来解决XOR问题,要求该前馈神经网络具有两个隐藏神经元和一个输出神经元,并使用ReLU作为激活函数
要解决XOR问题,首先要知道什么是XOR问题。
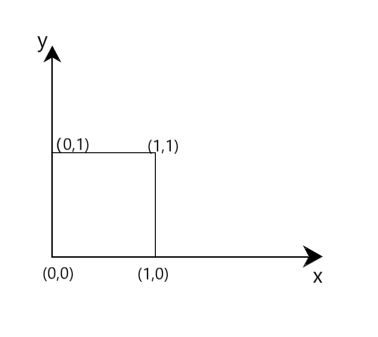
异或(XOR)问题可以看做是单位正方形的四个角,响应的输入模式为(0,0),(0,1),(1,1),(1,0)。第一个和第三个模式属于类0,即
![]()
和
![]() 。
。
输入模式(0,0)和(1,1)是单位正方形的两个相对的角,但它们产生相同的结果是0。另一方面,输入模式(0,1)和(1,0)是单位正方形另一对相对的角,但是它们属于类1,即
![]()
和
![]()
我们可以画一个图来更形象的看一下抑或问题
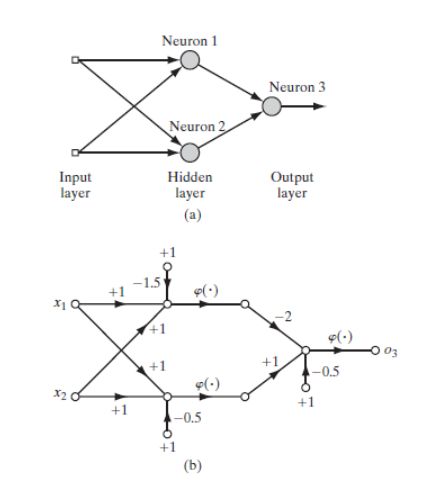
很显然,无法找出一条直线作为决策边界可以使(0,0)和(1,1)在一个区域,而(1,0)和(0,1)在另一个区域。然而,可以使用如下图所示的一层有两个隐藏神经元的隐藏层来解决异或问题。
代码实现:
先构建框架:
class Model_XOR(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Model_MLP_L2_V2, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
normal_(self.fc1.weight, mean=0., std=1.)
constant_(self.fc1.bias, val=0.0)
self.fc2 = nn.Linear(hidden_size, output_size)
normal_(self.fc2.weight, mean=0., std=1.)
constant_(self.fc2.bias, val=0.0)
self.act_fn = torch.relu()
# 前向计算
def forward(self, inputs):
z1 = self.fc1(inputs.float())
a1 = self.act_fn(z1)
z2 = self.fc2(a1)
a2 = self.act_fn(z2)
return a2然后进行模型训练并打印结果:
inputs = torch.Tensor([[0, 0], [0, 1], [1, 0], [1, 1]])
realy = torch.Tensor([[0], [1], [1], [0]])
# 设置模型
input_size = 2
hidden_size = 2
output_size = 1
model = Model_XOR(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
# 设置损失函数
loss_fn = nn.MSELoss()
# 设置优化器
learning_rate = 0.1
optimizer = torch.optim.SGD(lr=learning_rate, params=model.parameters())
# 其他参数
for epoch_num in range(1000):
out_y = model(inputs)
loss = loss_fn(out_y, realy) # 计算损失函数
optimizer.zero_grad() # 对梯度清零,避免造成累加
loss.backward() # 反向传播
optimizer.step() # 参数更新
input_test = inputs
out_test = model(input_test)
print('input_x', input_test.detach().numpy())
print('out_y', np.around(out_test.detach().numpy()))得到结果:
input_x [[0. 0.]
[0. 1.]
[1. 0.]
[1. 1.]]
out_y [[0.]
[1.]
[1.]
[0.]]
进程已结束,退出代码为 0
但是不是每次都是百分百正确,更多的结果是这样的。
input_x [[0. 0.]
[0. 1.]
[1. 0.]
[1. 1.]]
out_y [[0.]
[0.]
[0.]
[0.]]
进程已结束,退出代码为 0
我又调了学习率和训练次数发现问题还是没有解决,后面我把激活函数改成sigmoid得到的结果:
input_x [[0. 0.]
[0. 1.]
[1. 0.]
[1. 1.]]
out_y [[1.]
[0.]
[1.]
[0.]]
还是不对,不明白这是什么原因,希望老师下节课可以讲一讲。
这里纠正一下,激活函数变成sigmoid以后得到的结果是可以达到100%的,我做实验的时候学习率调低了,这里确实是懒了,一次没有全对就不想改了。隐藏层和输出层激活函数都是sigmoid是可以的,隐藏层是sigmoid输出层恒等也是可以的。
习题4-5 试举例说明死亡ReLU问题,并给出解决方法。
假设某层网络权重为 W ,输入为 x ,输出为 z ,经过 ReLU 激活后为 a 。设损失函数为 L 。对固定的学习率 lr ,梯度越大,权重 W 更新的越多:![]() 。
。
如果梯度太大,而学习率又不小心设置得太大,就会导致权重一下子更新过多,就有可能出现这种情况:对于任意训练样本 xi ,网络的输出都是小于0的。
此时,根据 ReLU 的激活函数:
![]()
这就会导致一种后果,我们以下面这个网络层举例:
对于上面的网络结构, W 为 2×4 的矩阵,单个训练样本 x 为 4×1 的向量。
假设这个时候的 W 是坏掉的,对所有的训练样本 x→ ,输出的这个 z1 始终是小于零的数。那么,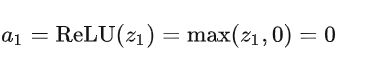
即,对于上面这个神经元,激活函数的输出始终为常数0 。回到前面的反向传播公式: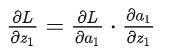
其中,由于 z1小于0时, a1 是常数 0。所以在 z1 小于0时始终有: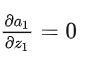
而:
这就出问题了,对于权重矩阵 W 的第一行的参数,在整个训练集上,损失函数对它的导数始终为零,也就是说,遍历了整个训练集,它的参数都没有更新。因此就说该神经元死了
关于解决死亡ReLU问题的方法在上次的实验中已经写过:
如何防止梯度消失?
sigmoid容易发生,更换激活函数为 ReLU即可。
权重初始化用高斯初始化
如何防止梯度爆炸?
1 设置梯度剪切阈值,如果超过了该阈值,直接将梯度置为该值。
2 使用ReLU,maxout等替代sigmoid
区别:
sigmoid函数值在[0,1],ReLU函数值在[0,+无穷],所以sigmoid函数可以描述概率,ReLU适合用来描述实数;
sigmoid函数的梯度随着x的增大或减小和消失,而ReLU不会。
Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。http://t.csdn.cn/RQtjx
这次我再搜索的时候发现一篇死亡relu复活的办法。
设某一个特定的ReLU激活单元R。R的上游还有很多影响R的输入分布的参数仍然会通过网络中其他路径获得更新。例如,R的同层的其他ReLU还处于激活状态同时也还在通过反向传播正常传递梯度。这些对R的上游参数的更新可能会使R的输入分布发生重要改变,让其回到正向区间(positive regime)内。其中的细节稍微有点复杂:在一个映射层(affine layer),那些直接为R提供输入的行向量会完全不会更新知道其被激。所以一个完全死亡的ReLU只能通过前一层的线性转换层(nolinear transformation layer)来复活。但是,如果线性转换层是一个没有参数共享的特定映射,第一个隐藏层(hiden layer)的死亡ReLU是一定无法复活的。
链接:http://t.csdn.cn/lR8zM
习题4-7 为什么在神经网络模型的结构化风险函数中不对偏置b进行正则化?
这个偏置 b 对于函数来说只是平移,并且 b 对输入的改变是不敏感的,无论输入变大还是变小, b 对结果的贡献只是一个偏置。因此其对过拟合没有帮助,并且在《DeepLearning》Chapter 7.1中说到:
对于神经网络正则化,一般只对每一层仿射变换的weights进行正则化惩罚,而不对偏置bias进行正则化。
相比于weight,bias训练准确需要的数据要更少。每个weight指定了两个变量之间的关系。weights训练准确需要在很多种情况下的同时观察两个变量。每个bias只控制一个变量。这意味着不对bias正则化,没有引入很多方差(variance)。同时,对bias进行正则化容易引起欠拟合。
从贝叶斯的角度来讲,正则化项通常都包含一定的先验信息,神经网络倾向于较小的权重以便更好地泛化,但是对偏置就没有这样一致的先验知识。另外,很多神经网络更倾向于区分方向信息(对应于权重),而不是位置信息(对应于偏置),所以对偏置加正则化项对控制过拟合的作用是有限的,相反很可能会因为不恰当的正则强度影响神经网络找到最优点。
参考链接:(17 条消息) 深度学习里面的偏置为什么不加正则? - 知乎 (zhihu.com)
习题4-8 为什么在用反向传播算法进行参数学习时要采用随机参数初始化的方式而不是直接令W=0,b=0?
若令 W=0,b=0 ,那么第一次计算时,隐层神经元的计算结果都一样,并且在反向传播时参数更新也一样,导致在每两层之间的参数都是一样的,这样相当于隐层只有 1 个神经元。因为如果参数都设为0,在第一遍前向计算的过程中所有的隐藏层神经元的激活值都相同。在反向传播时,所有权重更新也都相同,这样会导致隐藏层神经元没有区分性。这种现象称为对称权重现象。
上次的实验也写过这个问题,将w和b全部设为0后的结果是这样的:
The weights of the Layers:
('fc1.weight', Parameter containing:
tensor([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[0., 0., 0., 0., 0.]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([0.], requires_grad=True))
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.48750
[Train] epoch: 0/5, loss: 0.6931473016738892
The weights of the Layers:
('fc1.weight', Parameter containing:
tensor([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([0., 0., 0., 0., 0.], requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-0.0020, -0.0020, -0.0020, -0.0020, -0.0020]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([-0.0041], requires_grad=True))
The weights of the Layers:
('fc1.weight', Parameter containing:
tensor([[-2.2723e-05, 1.9955e-05],
[-2.2723e-05, 1.9955e-05],
[-2.2723e-05, 1.9955e-05],
[-2.2723e-05, 1.9955e-05],
[-2.2723e-05, 1.9955e-05]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([1.8309e-06, 1.8309e-06, 1.8309e-06, 1.8309e-06, 1.8309e-06],
requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-0.0038, -0.0038, -0.0038, -0.0038, -0.0038]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([-0.0077], requires_grad=True))
The weights of the Layers:
('fc1.weight', Parameter containing:
tensor([[-6.5808e-05, 5.7519e-05],
[-6.5808e-05, 5.7519e-05],
[-6.5808e-05, 5.7519e-05],
[-6.5808e-05, 5.7519e-05],
[-6.5808e-05, 5.7519e-05]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([4.8980e-06, 4.8980e-06, 4.8980e-06, 4.8980e-06, 4.8980e-06],
requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-0.0054, -0.0054, -0.0054, -0.0054, -0.0054]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([-0.0109], requires_grad=True))
The weights of the Layers:
('fc1.weight', Parameter containing:
tensor([[-0.0001, 0.0001],
[-0.0001, 0.0001],
[-0.0001, 0.0001],
[-0.0001, 0.0001],
[-0.0001, 0.0001]], requires_grad=True))
('fc1.bias', Parameter containing:
tensor([8.7562e-06, 8.7562e-06, 8.7562e-06, 8.7562e-06, 8.7562e-06],
requires_grad=True))
('fc2.weight', Parameter containing:
tensor([[-0.0069, -0.0069, -0.0069, -0.0069, -0.0069]], requires_grad=True))
('fc2.bias', Parameter containing:
tensor([-0.0137], requires_grad=True))
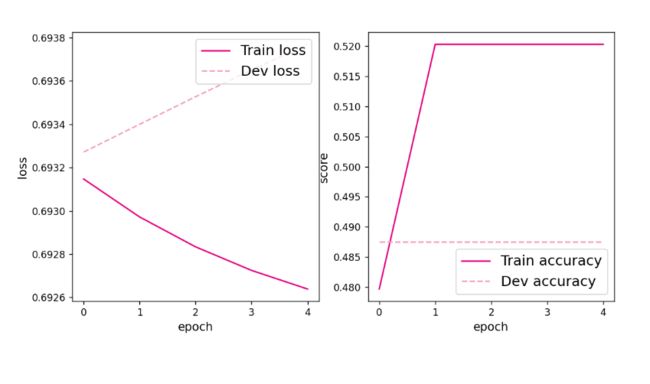
进程已结束,退出代码为 0从输出结果看,二分类准确率为50%左右,说明模型没有学到任何内容。训练和验证loss几乎没有怎么下降。
但是我们可以模型所有的权重w随机初始化,所有偏置b初始化为0。
在此情况下,在前向传播计算过程中:
a_1=g(w_{11} x_1+ w_{21}x_2), a_2=g(w_{12} x_1 + w_{22} x_2), a_3=sigmoid(w_{13} _1 +w_{23} _2)
在反向传播的过程中所有权重的导数都不相同,所以权重和偏置b都能得到更新。
但是模型所有权重w初始化为0,所有偏置b随机初始化是不可以的。
在此情况下,第一个batch前向传播:a1=g(1),a2=g(2),a3=sigmoid(3) ,在反向传播的过程中,由于 da1 与 da2 均为0,导致 dw11 dw12 dw21 dw22 均为0,则 w11 w12 w21 w22 得不到更新,为0,模型参数能够得到更新的只有 和w13 w23和b3 .
同理,在第二个batch在反向传播的过程中,由于 w13 和 w23 不为0,导致所有的参数都能够得到更新。这种方式存在更新较慢、梯度消失、梯度爆炸等问题,在实践中,通常不会选择此方式。
参考链接:谈谈神经网络权重为什么不能初始化为0 - 知乎 (zhihu.com)
习题4-9 梯度消失问题是否可以通过增加学习率来缓解?
我认为可以通过增加学习率来缓解梯度消失问题,但是不能解决梯度消失问题。
因为梯度消失不是指梯度太小,而是指的是梯度在最后一层往前传的过程中不断减小,这个消失,指的是最底层的梯度和最高层的梯度量级的差别。
如果你增大了lr,底层的学习可能确实更加有效了,高层的梯度就可能炸了。
那能不能每层设置不一样的lr呢,当然可以,adagrad就是这么做的,也确实有一定效果。
我在网上也看到一个特别形象的话来形容这个问题:人脾胃不好导致很瘦,营养不良。为了解决这个问题,每天吃很多东西,从一定程度上能缓解很瘦营养不良的问题,然而治标不治本。脾胃不好吸收差的病根仍然还在。所以很难根治。
总结
这次的作业有三个是上次做过的,但是毕竟上次的实验是整体的,并没有太过于深究这些问题,这次的作业中根据上次实验的基础增加了一些新的内容,这样可以对这些问题理解更深彻。
关于这次作业最让我不懂的就是习题4-2,有没有一种方法可以让正确率达到100%呢?
而这次作业最大的收获就是反向传播算法中参数的设置问题,虽然上次实验中已经得到权值和偏置不能全为0的结论,并且上手实验,但是这次的作业补充了理论知识,当w=0,b=0同一隐藏层所有神经元的输出都一致,对于后期不同的batch,每一隐藏层的权重都能得到更新,但是存在每一隐藏层的隐藏神经元权重都是一致的,多个隐藏神经元的作用就如同1个神经元。并且根据这个问题做出了拓展,了解了各种情况下的结果。