机器学习笔记-线性神经网络
1、线性神经网络原理
线性神经网络与感知器的主要区别在于感知器的激活函数只能输出两种可能值(-1或1),而线性神经网络的输出可以取任意值,其激活函数是线性函数。
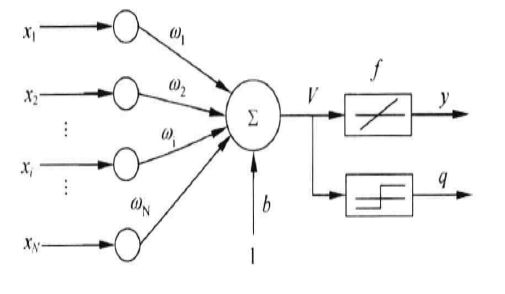
线性神经网络采用Widrow-Hoff学习规则(最小均方规则),即LMS(Least Mean Square)算法来调整网络的权值和偏置值。结构图如下。这里使用purelin激活函数进行模型训练,这样可以得到一个更好的效果。输出结果的时候还是使用sign激活函数。
x1,x2,xN为输入节点,w1,w2,wN为权向量,b为偏置因子,f为激活函数(purelin函数),神经网络的输出不仅产生二值输出以外(q),还可以产生模拟输出(y)。
2、Delta学习规则
Delta学习规则是一种利用梯度下降法的一般性的学习规则。
梯度下降法的问题:学习率难以选取,太大会产生震荡,太小收敛缓慢。容易陷入局部最优解。
3、解决异或问题
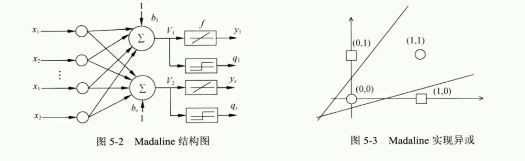
由于单层感知器不能解决异或问题,从而引入线性神经网络。可以用两条直线实现了异或问题。
另一个方法是对神经元添加非线性输入,引入非线性成分。如下图是我们解决异或问题的模型图,引入了非线性成分来解决。
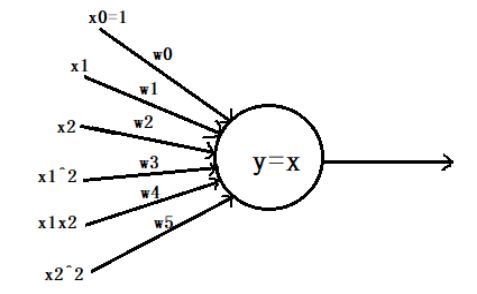
4、线性神经网络-异或问题(实现)
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
#输入数据
X=np.array([[1,0,0,0,0,0],
[1,0,1,0,0,1],
[1,1,0,1,0,0],
[1,1,1,1,1,1]])
#输入标签
Y=np.array([-1,1,1,-1])
#权值初始化,3行1列(3个输入1个输出),取值范围-1-1
W=(np.random.random(6)-0.5)*2
print(W)
#学习率
lr=0.11
#计算迭代次数
n=0
#神经网络的输出
O=0
def updata():
global X,Y,W,lr,n
n=n+1
O=np.dot(X,W.T)#激活函数y=x
W_C=lr*(Y-O.T).dot(X)/int(X.shape[0])#更新权值的平均值
W=W+W_C
for _ in range(1000):
updata()#更新权值
#正样本
x1=[0,1]
y1=[1,0]
#负样本
x2=[0,1]
y2=[0,1]
def calculate(x,root):
a=W[3]
b=W[2]+x*W[4]
c=W[0]+x*W[1]+x*x*W[3]
if root==1:
return (-b+np.sqrt(b*b-4*a*c))/(2*a)
if root==2:
return (-b-np.sqrt(b*b-4*a*c))/(2*a)
xdata=np.linspace(-1,2)
plt.figure()
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'b')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()
结果:
参考:https://blog.csdn.net/gulingfengze/article/details/78163425
参考:https://blog.csdn.net/xiaoming1999/article/details/121070288
参考视频:https://www.bilibili.com/video/BV1Rt411q7WJ?p=34&vd_source=166e4ef02c5e9ffa3f01c2406aec1508