【ML特征工程】第 4 章 :特征缩放的影响:从词袋到 Tf-Idf
大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流
个人主页-Sonhhxg_柒的博客_CSDN博客
欢迎各位→点赞 + 收藏⭐️ + 留言
系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟
文章目录
Tf-Idf:词袋的简单转折
TF-IDF 背后的直觉
进行测试
创建分类数据集
使用 Tf-Idf 转换扩展词袋
测试集上的特征缩放
逻辑回归分类
使用正则化调整 Logistic 回归
重要:比较模型时调整超参数
深潜:发生了什么?
TF-IDF = 列缩放
概括
词袋表示很容易生成,但远非完美。如果我们对所有单词进行平均计数,那么有些词最终被强调得比我们需要的更多。回忆一下第 3 章中艾玛和乌鸦的例子。我们想要一个强调两个主要角色的文档表示。“Emma”和“raven”这两个词都出现了三次,但“the”出现了八次,“and”出现了五次,“it”和“was”都出现了四次。仅仅通过简单的频率计数,主角并不能脱颖而出。这是有问题的。
挑选出诸如“华丽”、“闪闪发光”、“恐吓”、“暂时”和“统治”等词也很好,因为它们有助于设定段落的整体基调。它们表示情绪,这对数据科学家来说可能是非常有价值的信息。因此,理想情况下,我们想要一种能够突出显示有意义的词的表示。
Tf-Idf:词袋的简单转折
Tf-idf 是对词袋方法的简单改造。它代表词频——逆文档频率。tf-idf 不是查看数据集中每个文档中每个单词的原始计数,而是查看标准化计数,其中每个单词计数除以该单词出现的文档数。即:
bow( w , d ) = # 单词w在文档d中出现的次数
tf-idf( w , d ) = bow( w , d ) * N / (# w出现的文档)
N是数据集中文档的总数。分数N / (# documents ...) 就是所谓的逆文档频率。如果一个词出现在很多文档中,那么它的逆文档频率接近于1。如果一个词只出现在几个文档中,那么它的逆文档频率就会高很多。
或者,我们可以采取log 变换,而不是使用原始逆文档频率。对数将 1 变为 0,并使大数(远大于 1 的数)变小。(稍后会详细介绍。)
如果我们将 tf-idf 定义为:
tf-idf( w , d ) = bow( w , d ) * log ( N / # w出现的文档)
那么出现在每个文档中的单词将被有效地清零,而出现在极少数文档中的单词的计数将比以前更大。
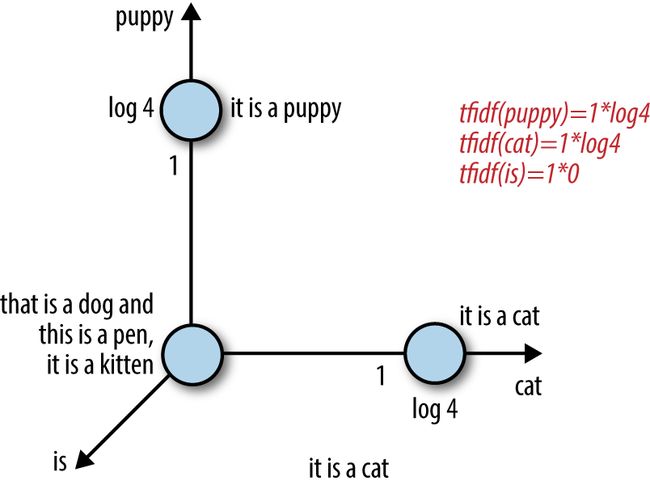
让我们看一些图片来了解它的全部内容。图 4-1显示了一个包含四个句子的简单示例:“it is a puppy”、“it is a cat”、“it is a kitten”和“that is a dog and this is a pen”。我们将这些句子绘制在三个词的特征空间中:“puppy”、“cat”和“is”。
现在让我们看一下 tf-idf 表示中的相同四个句子,使用逆向文档频率的对数变换。图 4-2显示了特征空间中的文档。请注意,“是”这个词作为一个特征被有效地消除了,因为它出现在这个数据集中的所有句子中。此外,因为它们每个只出现在四个句子中的一个句子中,所以“puppy”和“cat”这两个词现在的计数比以前高(log(4) = 1.38... > 1)。因此,tf-idf 使稀有词更加突出并有效地忽略了常见词。它与第 3 章中的基于频率的过滤方法密切相关,但在数学上比设置硬截止阈值要优雅得多。
TF-IDF 背后的直觉
Tf-idf 使稀有词更加突出并有效地忽略了常见词。
进行测试
tf-idf通过对word count特征进行改造乘以常数。因此,它是第 2 章介绍的特征缩放的一个例子。特征缩放在实践中的效果如何?让我们在一个简单的文本分类任务中比较缩放和未缩放特征的性能。是时候写一些代码了!
在示例 4-1中,我们重新访问了Yelp 评论数据集。Yelp 数据集挑战的第 6 轮包含对美国六个城市的近 160 万条企业评论。
示例 4-1。在 Python 中加载和清理 Yelp 评论数据集
>>> import json
>>> import pandas as pd
# Load Yelp business data
>>> biz_f = open('yelp_academic_dataset_business.json')
>>> biz_df = pd.DataFrame([json.loads(x) for x in biz_f.readlines()])
>>> biz_f.close()
# Load Yelp reviews data
>>> review_file = open('yelp_academic_dataset_review.json')
>>> review_df = pd.DataFrame([json.loads(x) for x in review_file.readlines()])
>>> review_file.close()
# Pull out only Nightlife and Restaurants businesses
>>> two_biz = biz_df[biz_df.apply(lambda x: 'Nightlife' in x['categories'] or
... 'Restaurants' in x['categories'],
... axis=1)]
# Join with the reviews to get all reviews on the two types of business
>>> twobiz_reviews = two_biz.merge(review_df, on='business_id', how='inner')
# Trim away the features we won't use
>>> twobiz_reviews = twobiz_reviews[['business_id',
... 'name',
... 'stars_y',
... 'text',
... 'categories']]
# Create the target column--True for Nightlife businesses, and False otherwise
>>> two_biz_reviews['target'] =\
... twobiz_reviews.apply(lambda x: 'Nightlife' in x['categories'],
... axis=1)创建分类数据集
让我们看看是否可以使用评论将企业归类为餐厅或夜生活场所。为了节省训练时间,我们可以提取一部分评论。在这种情况下,两个类别之间的评论计数存在很大差异。这称为类不平衡数据集。不平衡的数据集对于建模来说是有问题的,因为模型将花费大部分精力来适应更大的类别。由于我们在两个类别中都有大量数据,因此解决该问题的一个好方法是将较大类别(餐馆)的采样率降低到与较小类别(夜生活)大致相同的大小。这是一个示例工作流程:
-
随机抽取 10% 的夜生活评论和 2.1% 的餐厅评论(选择的百分比是为了使每个类别中的示例数量大致相等)。
-
创建此数据集的 70/30 训练测试拆分。在此示例中,训练集最终有 29,264 条评论,测试集有 12,542 条评论。
-
训练数据包含 46,924 个唯一单词;这是词袋表示中的特征数量。
例 4-2展示了我们是如何做到这一点的。
示例 4-2。创建平衡分类数据集
# Create a class-balanced subsample to play with
>>> nightlife = \
... twobiz_reviews[twobiz_reviews.apply(lambda x: 'Nightlife' in x['categories'],
... axis=1)]
>>> restaurants = \
... twobiz_reviews[twobiz_reviews.apply(lambda x: 'Restaurants' in x['categories'],
... axis=1)]
>>> nightlife_subset = nightlife.sample(frac=0.1, random_state=123)
>>> restaurant_subset = restaurants.sample(frac=0.021, random_state=123)
>>> combined = pd.concat([nightlife_subset, restaurant_subset])
# Split into training and test datasets
>>> training_data, test_data = modsel.train_test_split(combined,
... train_size=0.7,
... random_state=123)
>>> training_data.shape
(29264, 5)
>>> test_data.shape
(12542, 5)使用 Tf-Idf 转换扩展词袋
本实验的目的是比较词袋、tf-idf 和ℓ 2归一化的有效性分类。请注意,执行 tf-idf 然后执行ℓ 2归一化与单独执行ℓ 2归一化相同。因此,我们只需要测试三组特征:词袋、tf-idf 和词袋之上的逐字ℓ 2规范化。
在示例 4-3中,我们使用 scikit-learnCountVectorizer将评论文本转换为词袋。 所有文本特征化方法都隐含地依赖于分词器,分词器是将文本字符串转换为标记(单词)列表的模块。在此示例中,scikit-learn 的默认标记化模式查找两个或多个字母数字字符的序列。标点符号被视为标记分隔符。
示例 4-3。变换特征
# Represent the review text as a bag-of-words
>>> bow_transform = text.CountVectorizer()
>>> X_tr_bow = bow_transform.fit_transform(training_data['text'])
>>> X_te_bow = bow_transform.transform(test_data['text'])
>>> len(bow_transform.vocabulary_)
46924
>>> y_tr = training_data['target']
>>> y_te = test_data['target']
# Create the tf-idf representation using the bag-of-words matrix
>>> tfidf_trfm = text.TfidfTransformer(norm=None)
>>> X_tr_tfidf = tfidf_trfm.fit_transform(X_tr_bow)
>>> X_te_tfidf = tfidf_trfm.transform(X_te_bow)
# Just for kicks, l2-normalize the bag-of-words representation
>>> X_tr_l2 = preproc.normalize(X_tr_bow, axis=0)
>>> X_te_l2 = preproc.normalize(X_te_bow, axis=0)测试集上的特征缩放
关于特征缩放的一个微妙点是它需要知道特征统计那我们最在实践中可能不知道,例如均值、方差、文档频率,ℓ 2范数等。为了计算 tf-idf 表示,我们必须根据训练数据计算逆文档频率,并使用这些统计数据来缩放训练数据和测试数据。在 scikit-learn 中,将特征转换器拟合到训练数据上相当于收集相关统计数据。然后可以将安装的变压器应用于测试数据。
当我们使用训练统计数据来缩放测试数据时,结果看起来会有些模糊。测试集上的最小-最大缩放不再整齐地映射到 0 和1。ℓ 2范数、均值和方差统计数据看起来都有点偏差。这比丢失数据问题少。例如,测试集可能包含训练数据中不存在的词,我们没有文档频率可用于新词。常见的解决方案是简单地在测试集中删除新词。这似乎是不负责任的,但在训练集上训练的模型无论如何都不知道如何处理这些词。一个稍微不那么棘手的选择是明确学习一个“垃圾”词并将所有低频词映射到它,即使在训练集中,如“稀有词”中所讨论的.
逻辑回归分类
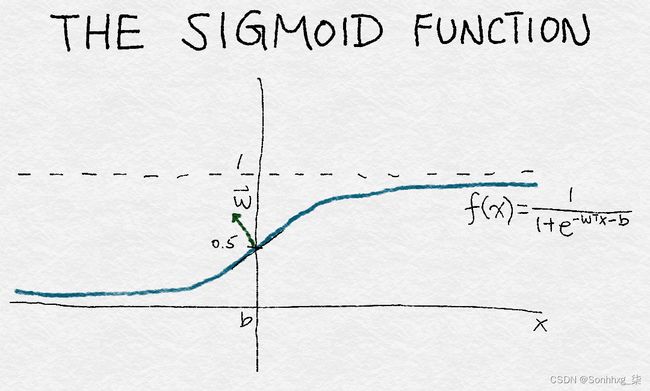
逻辑回归是一种简单的线性分类器。由于它的简单性,它通常是一个很好的第一个尝试的分类器。它采用输入特征的加权组合,并通过一个sigmoid 函数传递它,它平滑地将任何实数映射到 0 到 1 之间的数字。该函数将实数输入x转换为 0 到 1 之间的数字。它有一组参数w,表示围绕中点增加的斜率, 0.5。截距项b表示函数输出穿过中点的输入值。如果 sigmoid 输出大于 0.5,逻辑分类器将预测正类,否则预测负类。通过改变w和b,人们可以控制决策发生变化的位置,以及决策应该以多快的速度响应围绕该点变化的输入值。
图 4-3说明了 sigmoid 函数。
现在让我们在各种特征集上构建一些简单的逻辑回归分类器,看看他们是怎么做的(例 4-4)。
示例 4-4。使用默认参数训练逻辑回归分类器
>>> def simple_logistic_classify(X_tr, y_tr, X_test, y_test, description):
... ### Helper function to train a logistic classifier and score on test data
... m = LogisticRegression().fit(X_tr, y_tr)
... s = m.score(X_test, y_test)
... print ('Test score with', description, 'features:', s)
... return m
>>> m1 = simple_logistic_classify(X_tr_bow, y_tr, X_te_bow, y_te, 'bow')
>>> m2 = simple_logistic_classify(X_tr_l2, y_tr, X_te_l2, y_te, 'l2-normalized')
>>> m3 = simple_logistic_classify(X_tr_tfidf, y_tr, X_te_tfidf, y_te, 'tf-idf')
Test score with bow features: 0.775873066497
Test score with l2-normalized features: 0.763514590974
Test score with tf-idf features: 0.743182905438矛盾的是,结果表明最准确的分类器是使用 BoW 特征的分类器。这是出乎意料的。事实证明,原因是分类器没有很好地“调整”,这是比较分类器时常见的错误。
使用正则化调整 Logistic 回归
逻辑回归有一些花里胡哨的东西。当特征的数量大于数据点的数量时,寻找最佳模型的问题被称为欠定的。解决此问题的一种方法是对训练过程施加额外的约束。这称为正则化,其技术细节在此处讨论。
大多数逻辑回归的实现都允许正则化。为了使用此功能,必须指定一个正则化参数。正则化参数是在模型训练过程中不会自动学习的超参数。相反,它们必须根据手头的问题进行调整,并提供给训练算法。此过程称为超参数调整。(有关如何评估机器学习模型的详细信息,请参阅 Zheng [2015]。)调整超参数的一种基本方法称为网格搜索:您指定超参数值的网格,调谐器以编程方式搜索最佳超参数设置网格。找到最佳超参数设置后,您可以使用该设置在整个训练集上训练模型,并将其在测试集上的性能作为对此类模型的最终评估。
重要:比较模型时调整超参数
在比较模型或特征时调整超参数至关重要。软件包的默认设置总是会返回一个模型。但除非软件在后台执行自动调整,否则它很可能会返回基于次优超参数设置的次优模型。分类器性能对超参数设置的敏感性取决于模型和训练数据的分布。逻辑回归对超参数设置相对稳健(或不敏感)。即便如此,有必要找到并使用正确范围的超参数。否则,一种模型相对于另一种模型的优势可能完全取决于调整参数,而不会反映模型或特征的实际行为。
即使是最好的自动调谐包仍然需要指定搜索的上限和下限,而找到这些限制可能需要手动尝试几次。
在下面的示例中,我们手动将逻辑正则化参数的搜索网格设置为 {1e-5, 0.001, 0.1, 1, 10, 100}。上限和下限尝试了几次以缩小范围。表 4-1给出了每个特征集的最佳超参数设置。
| ℓ 2正则化 | |
|---|---|
| BoW | 0.1 |
| ℓ2-normalized | 10 |
| Tf-idf | 0.001 |
我们还想测试 tf-idf 和 BoW 之间的准确性差异是否是由于噪声造成的。为此,我们使用k次交叉验证来模拟具有多个统计独立的数据集。它将数据集分成k份。交叉验证过程遍历折叠,使用除一个折叠之外的所有折叠进行训练,并验证保留的折叠的结果。
通过重采样估计方差
现代统计方法假设基础数据来自随机分布。源自数据的模型的性能测量也受到随机噪声的影响。在这种情况下,基于可比较统计数据的数据集,不仅进行一次测量,而且进行多次测量始终是一个好主意。这为我们提供了测量的置信区间。
k折交叉验证就是这样一种策略。重采样是另一种从同一基础数据集生成多个小样本的技术。有关重采样的更多详细信息,请参见 Zheng (2015)。
GridSearchCVscikit-learn运行中的函数网格搜索使用交叉验证(参见示例 4-5)。图 4-4显示了在每个特征集上训练的模型的精度测量分布的盒须图。盒子中的中间线标记了中值精度,盒子本身标记了第一和第三四分位数之间的区域,而胡须扩展到分布的其余部分。
示例 4-5。使用网格搜索调整逻辑回归超参数
>>> import sklearn.model_selection as modsel
# Specify a search grid, then do a 5-fold grid search for each of the feature sets
>>> param_grid_ = {'C': [1e-5, 1e-3, 1e-1, 1e0, 1e1, 1e2]}
# Tune classifier for bag-of-words representation
>>> bow_search = modsel.GridSearchCV(LogisticRegression(), cv=5,
... param_grid=param_grid_)
>>> bow_search.fit(X_tr_bow, y_tr)
# Tune classifier for L2-normalized word vector
>>> l2_search = modsel.GridSearchCV(LogisticRegression(), cv=5,
... param_grid=param_grid_)
>>> l2_search.fit(X_tr_l2, y_tr)
# Tune classifier for tf-idf
>>> tfidf_search = modsel.GridSearchCV(LogisticRegression(), cv=5,
... param_grid=param_grid_)
>>> tfidf_search.fit(X_tr_tfidf, y_tr)
# Let's check out one of the grid search outputs to see how it went
>>> bow_search.cv_results_
{'mean_fit_time': array([ 0.43648252, 0.94630651,
5.64090128, 15.31248307, 31.47010217, 42.44257565]),
'mean_score_time': array([ 0.00080056, 0.00392466, 0.00864897, 0 .00784755,
0.01192751, 0.0072515 ]),
'mean_test_score': array([ 0.57897075, 0.7518111 , 0.78283898, 0.77381766,
0.75515992, 0.73937261]),
'mean_train_score': array([ 0.5792185 , 0.76731652, 0.87697341, 0.94629064,
0.98357195, 0.99441294]),
'param_C': masked_array(data = [1e-05 0.001 0.1 1.0 10.0 100.0],
mask = [False False False False False False],
fill_value = ?),
'params': ({'C': 1e-05},
{'C': 0.001},
{'C': 0.1},
{'C': 1.0},
{'C': 10.0},
{'C': 100.0}),
'rank_test_score': array([6, 4, 1, 2, 3, 5]),
'split0_test_score': array([ 0.58028698, 0.75025624, 0.7799795 , 0.7726341 ,
0.75247694, 0.74086095]),
'split0_train_score': array([ 0.57923964, 0.76860316, 0.87560871, 0.94434003,
0.9819308 , 0.99470312]),
'split1_test_score': array([ 0.5786776 , 0.74628396, 0.77669571, 0.76627371,
0 .74867589, 0.73176149]),
'split1_train_score': array([ 0.57917218, 0.7684849 , 0.87945837, 0.94822946,
0.98504976, 0.99538678]),
'split2_test_score': array([ 0.57816504, 0.75533914, 0.78472578, 0.76832394,
0.74799248, 0.7356911 ]),
'split2_train_score': array([ 0.57977019, 0.76613558, 0.87689548, 0.94566657,
0.98368288, 0.99397719]),
'split3_test_score': array([ 0.57894737, 0.75051265, 0.78332194, 0.77682843,
0.75768968, 0.73855092]),
'split3_train_score': array([ 0.57914745, 0.76678626, 0.87634546, 0.94558346,
0.98385443, 0.99474628]),
'split4_test_score': array([ 0.57877649, 0.75666439, 0.78947368, 0.78503076,
0.76896787, 0.75 ]),
'split4_train_score': array([ 0.57876303, 0.7665727 , 0.87655903, 0.94763369,
0.98334188, 0.99325132]),
'std_fit_time': array([ 0.03874582, 0.02297261, 1.18862097, 1.83901079,
4.21516797, 2.93444269]),
'std_score_time': array([ 0.00160112, 0.00605009, 0.00623053, 0.00698687,
0.00713112, 0.00570195]),
'std_test_score': array([ 0.00070799, 0.00375907, 0.00432957, 0.00668246,
0.00612049]),
'std_train_score': array([ 0.00032232, 0.00102466, 0.00131222, 0.00143229,
0.00100223, 0.00073252])}
# Plot the cross validation results in a box-and-whiskers plot to
# visualize and compare classifier performance
>>> search_results = pd.DataFrame.from_dict({
... 'bow': bow_search.cv_results_['mean_test_score'],
... 'tfidf': tfidf_search.cv_results_['mean_test_score'],
... 'l2': l2_search.cv_results_['mean_test_score']
... })
# Our usual matplotlib incantations. Seaborn is used here to make
# the plot pretty.
>>> import matplotlib.pyplot as plt
>>> import seaborn as sns
>>> sns.set_style("whitegrid")
>>> ax = sns.boxplot(data=search_results, width=0.4)
>>> ax.set_ylabel('Accuracy', size=14)
>>> ax.tick_params(labelsize=14)表 4-2显示了每个超参数设置的平均交叉验证分类器准确度。每列中的星号表示该特征集达到的最高准确度。
| 正则化参数 | BoW | ℓ 2 -归一化 | Tf-idf |
|---|---|---|---|
| 0.00001 | 0.578971 | 0.575724 | 0.721638 |
| 0.001 | 0.751811 | 0.575724 | 0.788648 * |
| 0.1 | 0.782839 * | 0.589120 | 0.763566 |
| 1 | 0.773818 | 0.734247 | 0.741150 |
| 10 | 0.755160 | 0.776756 * | 0.721467 |
| 100 | 0.739373 | 0.761106 | 0.712309 |
ℓ 2 个归一化特征的结果在图 4-4中看起来非常糟糕。但不要被愚弄了。精度低的数字是由于非常糟糕的正则化参数设置——次优的超参数会导致非常错误的结论的具体证据。如果我们使用每个特征集的最佳超参数设置来训练模型,如示例 4-6 所示,不同特征集的准确率分数非常接近。
示例 4-6。比较不同特征集的最后训练和测试步骤
# Train a final model on the entire training set, using the best hyperparameter
# settings found previously. Measure accuracy on the test set.
>>> m1 = simple_logistic_classify(X_tr_bow, y_tr, X_te_bow, y_te, 'bow',
... _C=bow_search.best_params_['C'])
>>> m2 = simple_logistic_classify(X_tr_l2, y_tr, X_te_l2, y_te, 'l2-normalized',
... _C=l2_search.best_params_['C'])
>>> m3 = simple_logistic_classify(X_tr_tfidf, y_tr, X_te_tfidf, y_te, 'tf-idf',
... _C=tfidf_search.best_params_['C'])
Test score with bow features: 0.78360708021
Test score with l2-normalized features: 0.780178599904
Test score with tf-idf features: 0.788470738319适当的调整提高了所有特征集的准确性,现在这三个特征集在正则化逻辑回归下都产生了相似的分类准确性。tf-idf 模型的准确度分数略高,但差异可能不具有统计显着性。这些结果完全令人费解。如果特征缩放并不比普通的词袋更好,那为什么还要这样做呢?如果 tf-idf 什么都不做,为什么要大声疾呼?我们将在下一节探讨这些问题的答案。
深潜:发生了什么?
为了理解结果背后的“原因”,我们必须查看模型如何使用这些特征。对于像逻辑回归这样的线性模型,这是通过称为数据矩阵的中间对象发生的。
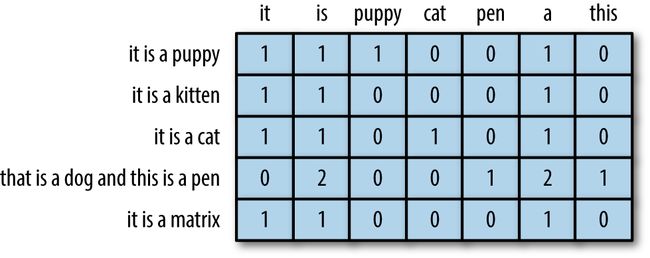
数据矩阵包含表示为固定长度平面向量的数据点。对于词袋向量,数据矩阵是也称为文档术语矩阵。图 3-1以向量形式显示了一个词袋向量,图 4-1说明了特征空间中的四个词袋向量。要形成一个文档术语矩阵,只需将文档向量平放,然后将它们堆叠在一起。列代表词汇表中所有可能的词(见图 4-5)。由于大多数文件仅包含所有可能单词的一小部分,该矩阵中的大部分条目都是零;它是一个稀疏矩阵。
特征缩放方法本质上是对数据矩阵的列操作。特别是,tf-idf 和ℓ 2归一化都将整个列(例如n- gram 特征)乘以一个常数。
TF-IDF = 列缩放
Tf-idf 和ℓ 2归一化都是对数据矩阵的列操作。
正如附录 A中所讨论的,训练线性分类器归结为找到特征的最佳线性组合,这些特征是数据矩阵的列向量。解空间的特征在于数据矩阵的列空间和零空间。训练好的线性分类器的质量直接取决于零空间和数据矩阵的列空间。大的列空间意味着特征之间几乎没有线性相关性,这通常是好的。零空间包含不能表示为现有数据的线性组合的“新”数据点;大的零空间可能会有问题。(细读附录 A强烈建议读者阅读线性决策曲面、特征分解和矩阵的基本子空间等概念。)
列缩放操作如何影响数据矩阵的列空间和零空间?答案是“不是很多”。但是 tf-idf 和ℓ 2标准化可能不同的可能性很小。我们现在来看看为什么。
由于几个原因,数据矩阵的零空间可能很大。首先,许多数据集包含彼此非常相似的数据点。这意味着与数据集中的数据点数相比,有效行空间较小。其次,特征的数量可能远大于数据点的数量。词袋特别擅长创建巨大的特征空间。在我们的 Yelp 示例中,训练集中的 29,000 条评论中有 47,000 个特征。此外,不同单词的数量通常随着数据集中文档的数量而增长,因此添加更多文档不一定会降低特征数据比或减少零空间。
对于词袋,与特征数量相比,列空间相对较小。可能有些词在相同文档中出现的次数大致相同。这将导致相应的列向量几乎是线性相关的,从而导致列空间不像它可能的那样满秩(有关满秩的定义,请参见附录 A)。这称为秩不足。(就像动物缺乏维生素和矿物质一样,矩阵可能缺乏秩,输出空间不会像它应该的那样蓬松。)
秩不足的行空间和列空间导致模型为该问题提供过多。线性模型为数据集中的每个特征配备了一个权重参数。如果行和列空间是满秩1 ,那么该模型将允许我们在输出空间中生成任何目标向量。当它们排名不足时,模型的自由度超过了它的需要。这使得确定解决方案变得更加困难。
特征缩放能否解决数据矩阵的秩不足问题?让我们来看看。
列空间定义为所有列向量的线性组合(粗体表示向量):a 1 v 1 + a 2 v 2 + ... + a n v n。特征缩放用常数倍数替换列向量,比如说˜1=C1. 但是我们仍然可以通过将1替换为来生成原始的线性组合一个˜1=一个1/C. 似乎特征缩放不会改变列空间的等级。类似地,特征缩放不影响零空间的等级,因为可以通过反向缩放权重向量中的相应条目来抵消缩放后的特征列。
然而,像往常一样,有一个陷阱。如果标量为0,则无法恢复原来的线性组合;v 1不见了。如果该向量与所有其他列线性无关,那么我们就有效地缩小了列空间并扩大了零空间。
如果该向量与目标输出不相关,那么这可以有效地去除噪声信号,这是一件好事。事实证明,这是 tf-idf 和ℓ 2归一化之间的关键区别。ℓ 2归一化永远不会计算零范数,除非向量包含全零。如果向量接近于零,则其范数也接近于零。除以小范数会突出向量并使其更长。
另一方面,Tf-idf 可以生成接近于零的比例因子,如图 4-2所示。当单词出现在训练集中的大量文档中时,就会发生这种情况。这样的词可能与目标向量没有很强的相关性。将其修剪掉可以让求解器专注于列空间中的其他方向并找到更好的解决方案(尽管精度的提高可能不会很大,因为通常很少有噪声方向可以通过这种方式修剪)。
特征缩放——ℓ 2和 tf-idf——确实对求解器的收敛速度有明显影响。这表明数据矩阵现在具有更小的条件数(最大和最小奇异值之间的比率——有关这些术语的完整讨论,请参见附录 A)。事实上,ℓ 2归一化使条件数接近1。但并不是说条件数越好,解就越好。在这个实验中,ℓ 2归一化比 BoW 或 tf-idf 收敛得快得多。但它对过度拟合也更敏感:它需要更多的正则化并且对优化期间的迭代次数更敏感。
概括
在本章中,我们使用 tf-idf 作为切入点来详细分析特征转换如何影响(或不影响)模型。Tf-idf 是特征缩放的一个例子,因此我们将其性能与另一种特征缩放方法——ℓ 2归一化进行了对比。
结果并不像人们预期的那样。Tf-idf 和ℓ 2归一化不会提高最终分类器的准确度,高于普通词袋。在获得一些统计建模和线性代数印章后,我们明白了原因:它们都没有改变数据矩阵的列空间。
两者之间的一个小区别是 tf-idf 可以“拉伸”字数,也可以“压缩”它。换句话说,它使一些计数更大,而另一些则接近于零。因此,tf-idf 可以完全消除无信息的词。
在此过程中,我们还发现了特征缩放的另一个效果:它改善了数据矩阵的条件数,使线性模型的训练速度更快。ℓ 2归一化和 tf-idf 都有这个效果。
总而言之,教训是:正确的特征缩放有助于分类。正确的缩放比例会突出提供信息的词并降低常用词的权重。它还可以提高数据矩阵的条件数。正确的缩放比例不一定是统一的列缩放比例。
这个故事很好地说明了在一般情况下分析特征工程效果的难度。改变特征会影响训练过程和随之而来的模型。线性模型是最容易理解的模型,但它仍然需要非常仔细的实验方法和大量深厚的数学知识来梳理理论和实践影响。对于更复杂的模型或特征转换,这几乎是不可能的。