点云配准——经典配准算法及配准效果对比
目录
点云配准基础知识
什么是点云配准?
点云配准的步骤
粗配准
精配准
点云配准的经典算法
ICP算法
NDT算法
3DSC算法
PFH
FPFH
完全配准效果对比
点云配准基础知识
什么是点云配准?
点云配准技术即是通过寻找不同视角下不同点云之间的映射关系,利用一定的算法将同一目标场景的不同点云转换到同一个坐标系下,形成更完整的点云的过程。3D点云配准是是点云处理技术的一个重要组成部分。
如何使点云配准方法更加快速准确 已成为一个点云研究的热点和难点。 点云配准要应对点云数据的无序性、非结构化、不均匀和噪声等干扰。如何有效地利用已有的信息实现精确、鲁棒的点云配准算法具有重要的研究意义和价值。
点云配准的阶段
点云配准分为粗配准(Coarse Registration)和精配准(Fine Registration)两个阶段。
点云配准的过程就是矩阵变换的过程。
粗配准
粗配准是在源点云与目标点云完全不知道任何初始相对位置的情况下,所进行的配准方法。该方法的主要目的是在初始条件未知的情况下,快速估算一个大致的点云配准矩阵。对于任意初始状态的两片点云,使得两片点云大致对齐,给旋转矩阵R和平移向量T提供初值。
整个计算过程要求比较高的计算速度,对于计算结果的精确度则不做过高的要求。
常见的粗配准算法的思路包括了:基于局部特征描述的方法、基于全局搜索策略以及通过统计学概率等方法。
精配准
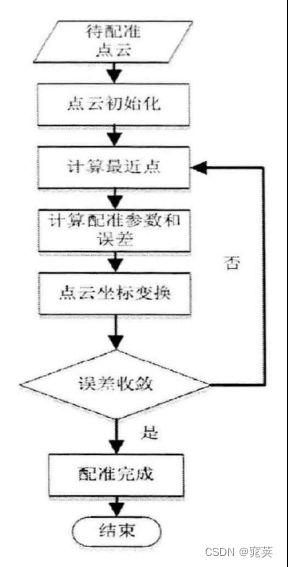
精配准是在粗配准的基础上,进行更精确、更细化的配准。精配准是利用已知的初始变换矩阵,通过迭代最近点算法(ICP算法)等计算得到较为精确的解。精配准流程图如下:
点云配准的经典算法
ICP算法
ICP(迭代式最近点)Iterative Closest Point 算法是.1992年Besl 和 Mckay等人在1992年提出的,作为三维点云配准中最基本且最经典的方法,算法以点到平面或点到点的距离为优化目标,通过不停迭代来估计源点云和目标点云间的刚体变换矩阵。
ICP算法通过计算源点云与目标点云对应点距离,构造旋转平移矩阵RT,通过RT对源点云变换,计算变换之后的均方差。若均方差满足阈值条件,则算法结束。否则则继续重复迭代直至误差满足阈值条件或者迭代次数终止。
论文: P.J.Besl,N.D.McKay.A method for registration of 3d shapes[J].IEEE Trans.on Pattern Anal
ysis and Machine Intelligence,1992,14(2):239256
优点:配准结果精确度较高,是一种精确配准算法;
缺点:对于两片点云的初始位置要求较为严格,否则容易陷入局部收敛且会影响配准速度,因此需要通过粗配准来为ICP提供较好的点云初始位置。
NDT算法
正态分布算法(NDT)利用统计学概率的方法,根据点云正态分布情况,确定了对应点对从而计算源点云与目标点云之间的变换关系。它是一种离散的全局配准算法,它在离散化坐标空间中,通过最大化源点在目标点体素化后计算出的正态分布的概率密度上的得分进行配准。利用概率密度函数和最优求解方法来计算待配准点云之间的转换关系。
优点:相较于ICP 算法,NDT 算法在很大程度上降低了配准算法的运行时间,降低了配准误差,提高了配准精度。
缺点:要对所有的点云数据进行网格化处理,因此对于范围大、点云密集的场景中的配准耗时。
3DSC算法
2004年Frome等提出了三维形状上下文(3DSC)描述符用来点云配准,使用特征直方图的方式来统计点云表面轮廓上的点的分布情况。
优点:对非刚性物体的配准有利
缺点:但对物体内部易形变的模型配准鲁棒性不好
PFH
Rusu在2008年提出基于点特征直方图(PFH)Point Feature Histogram的配准算法。PFH是通过构建特征点及其邻域点之间法向量的差异性关系,并把这种关系参数化组成一个多维向量直方图。这一个多维向量就可以代表特征点周围的几何关系。PFH通过法向量之间的夹角关系描述特征点及其邻域空间区域内模型表面的几何特征。因此,特征点及其邻域内点的法向量计算质量的好坏直接决定了这个空间信息描述的质量。
论文:Rusu R B , Blodow N , Marton Z C , et al. Aligning Point Cloud Views using Persistent Feature Histograms[C]// 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, September 22-26, 2008, Acropolis Convention Center, Nice,France:IEEE, 2008:325-338.
优点:对于邻域的几何特征表述是足够充分的
缺点:算法的复杂度太大
FPFH
Rusu在2009年提出快速点特征直方图(FPFH)Fast Point Feature Histogram 的配准算法。该方法是将关键点邻域内每一对点建立达布坐标系(darboux frame),计算法向量与坐标系的夹角,形成能描述关键点邻域关系的直方图。
FPFH是一种常见的基于局部特征描述的方法,基于局部特征描述的方法是通过提取源点云与目标点云的邻域几何特征,通过几何特征快速确定二者之间的点对的对应关系,再计算此关系进而获得变换矩阵。
论文:Rusu R B , Blodow N , Beetz M . Fast Point Feature Histograms (FPFH) for 3D registration[C]// Robotics and Automation, 2009. ICRA '09. IEEE International Conference on. IEEE, 2009.
优点:算法简单、计算速度快
缺点:抗噪性差
完全配准效果对比
软硬件环境配置:
CPU:intel corei7-12650H
显卡:Nvidia GeForce RTX 3050
内存:16GB
操作系统:Windows 11
开发环境:Vs2019 +pcl1.12.0(release)
点云配准数据集:不同角度下的bunny rabbit
ndt+icp 3dsc+icp
pfh+icp fpfh+icp
| 配准方案 |
配准时间 |
x轴 旋转误差 |
y轴 旋转误差 |
z轴 旋转误差 |
x轴 平移误差 |
y轴 平移误差 |
z轴 平移误差 |
| ndt+icp |
1.633s |
0 |
-0.003923 |
-0.78539 |
0.0008968 |
-0.3 |
-0.2 |
| 3dsc+icp |
146.513s |
0.476954 |
0.474738 |
0.107566 |
0.0153899 |
-0.282554 |
-0.0507123 |
| pfh+icp |
25.391s |
0.480662 |
0.46401 |
-0.67673 |
-0.015307 |
-0.28634 |
-0.149036 |
| fpfh+icp |
6.074s |
0.477056 |
0.469924 |
0.110106 |
-0.015499 |
-0.28634 |
-0.149036 |