DKT单元
前言:本文主要介绍离散基尔霍夫理论(DKT, Discrete Kirchhoff Theory),包括其三角板单元的插值函数、刚度矩阵的推导以及薄板弯曲算例。
位移插值函数
根据横向剪切应变板的小变形假定,板的位移场可以表述为:
u = − z φ x , y = − z φ y , w = w (1) u=-z\varphi_{x },y=-z\varphi_{y },w=w \tag{1} u=−zφx,y=−zφy,w=w(1)
式中, φ x , φ y \varphi_{x },\varphi_{y } φx,φy为绕中面的转动变量,在Kirchhoff板理论中, φ x = ∂ w ∂ x , φ y = ∂ w ∂ y \varphi_{x }=\frac{\partial w}{\partial x} , \varphi_{y }=\frac{\partial w}{\partial y} φx=∂x∂w,φy=∂y∂w。
如图所示,在六节点三角板单元中,节点4,5,6为各边中点。 n , τ n ,\tau n,τ分别为边界的法线和切线, θ \theta θ为法线 n n n和 x x x正向的夹角。

对单元内转动变量进行二次插值
φ x = ∑ i = 1 6 N i φ x i , φ y = ∑ i = 1 6 N i φ y i (2) \varphi_{x}=\sum_{i=1}^{6} N_{i} \varphi_{x i}, \varphi_{y}=\sum_{i=1}^{6} N_{i} \varphi_{y i} \tag{2} φx=i=1∑6Niφxi,φy=i=1∑6Niφyi(2)
在各节点处,引入Kirchhoff直法线假设:
角结点处:
{ ( ∂ w ∂ x ) i − φ x i = 0 ( ∂ w ∂ y ) i − φ y i = 0 ( i = 1 , 2 , 3 ) (3) \left\{\begin{array}{l} \left(\frac{\partial w}{\partial x}\right)_{i}-\varphi_{x i}=0 \\ \left(\frac{\partial w}{\partial y}\right)_{i}-\varphi_{y i}=0 \end{array}\right. \quad(i=1,2,3) \tag{3} {(∂x∂w)i−φxi=0(∂y∂w)i−φyi=0(i=1,2,3)(3)
中点处:
{ ( ∂ w ∂ τ ) k − φ τ k = 0 φ n k = 1 2 ( φ n i + φ n j ) ( k = 4 , 5 , 6 ) (4) \left\{\begin{array}{l} \left(\frac{\partial w}{\partial \tau}\right)_{k}-\varphi_{\tau k}=0 \\ \varphi_{n k}=\frac{1}{2}\left(\varphi_{n i}+\varphi_{n j}\right) \end{array}\right. \quad(k=4,5,6) \tag{4} {(∂τ∂w)k−φτk=0φnk=21(φni+φnj)(k=4,5,6)(4)
对边 i j ij ij任意点的挠度进行 H e r m i t e Hermite Hermite插值得:
w = H i 1 w i + H j 1 w j + H i 2 ( ∂ w ∂ τ ) i + H j 2 ( ∂ w ∂ τ ) j (5) w = {H_{i1}}{w_i} + {H_{j1}}{w_j} + {H_{i2}}{\left( {\frac{{\partial w}}{{\partial \tau }}} \right)_i} + {H_{j2}}{\left( {\frac{{\partial w}}{{\partial \tau }}} \right)_j} \tag{5} w=Hi1wi+Hj1wj+Hi2(∂τ∂w)i+Hj2(∂τ∂w)j(5)
式中: H i 1 = ( 1 + 2 τ l i j ) ( τ − l i j l i j ) 2 {H_{i1}}{\rm{ = }}\left( {{\rm{1 + }}\frac{{2\tau }}{{{l_{ij}}}}} \right){\left( {\frac{{\tau - {l_{ij}}}}{{{l_{ij}}}}} \right)^2} Hi1=(1+lij2τ)(lijτ−lij)2, H i 2 = τ ( τ − l i j l i j ) 2 {H_{i2}}{\rm{ = }}\tau {\left( {\frac{{\tau - {l_{ij}}}}{{{l_{ij}}}}} \right)^2} Hi2=τ(lijτ−lij)2, H j 1 = ( 1 − 2 τ − l i j l i j ) ( τ l i j ) 2 {H_{j1}}{\rm{ = }}\left( {{\rm{1}} - {\rm{2}}\frac{{\tau - {l_{ij}}}}{{{l_{ij}}}}} \right){\left( {\frac{\tau }{{{l_{ij}}}}} \right)^2} Hj1=(1−2lijτ−lij)(lijτ)2, H j 2 = ( τ − l i j ) ( τ l i j ) 2 {H_{j2}}{\rm{ = }}\left( {\tau - {l_{ij}}} \right){\left( {\frac{\tau }{{{l_{ij}}}}} \right)^2} Hj2=(τ−lij)(lijτ)2, l i j l_{ij} lij为边 i j ij ij的长度.。
将式(5)两边对 τ \tau τ求导,并将 τ = l i j / 2 \tau=l_{ij}/2 τ=lij/2代入可以得到:
( ∂ w ∂ τ ) k = − 3 2 l i j w i + 3 2 l i j w j − 1 4 ( ∂ w ∂ τ ) i − 1 4 ( ∂ w ∂ τ ) j (6) {\left( {\frac{{\partial w}}{{\partial \tau }}} \right)_k} = - \frac{3}{{2{l_{ij}}}}{w_i} + \frac{3}{{2{l_{ij}}}}{w_j} - \frac{1}{4}{\left( {\frac{{\partial w}}{{\partial \tau }}} \right)_i} - \frac{1}{4}{\left( {\frac{{\partial w}}{{\partial \tau }}} \right)_j}\tag{6} (∂τ∂w)k=−2lij3wi+2lij3wj−41(∂τ∂w)i−41(∂τ∂w)j(6)
边界局部坐标转动变量和整体坐标转动变量存在如下关系:
[ φ n φ τ ] = [ cos θ sin θ − sin θ cos θ ] [ φ x φ y ] (7) \left[ {\begin{array}c \varphi _n\\ \varphi _\tau \end{array}} \right] = \begin{bmatrix} \cos \theta &\sin \theta \\ -\sin \theta &\cos \theta \end{bmatrix} \begin{bmatrix} {{\varphi _x}}\\{{\varphi _y}} \end{bmatrix} \tag{7} [φnφτ]=[cosθ−sinθsinθcosθ][φxφy](7)
由式(3)、(4)、(6)以及(7),可以得到如下关系:
[ cos θ i j sin θ i j − sin θ i j cos θ i j ] [ φ x k φ y k ] = [ 0 cos θ i j 2 sin θ i j 2 0 cos θ i j 2 sin θ 2 θ i j − 3 2 l i j sin θ i j 4 − cos θ i j 4 3 2 l i j sin θ i j 4 − cos θ i j 4 ] [ w i φ x i φ y i w j φ x j φ y j ] T ( 8 ) \begin{bmatrix} \cos \theta_{ij} &\sin \theta_{ij} \\ -\sin \theta_{ij} &\cos \theta_{ij} \end{bmatrix} \begin{bmatrix} {{\varphi _{xk}}}\\ {{\varphi _{yk}}} \end{bmatrix} = \begin{bmatrix} 0&{\frac{{\cos {\theta _{ij}}}}{2}}&{\frac{{\sin {\theta _{ij}}}}{2}}&0&{\frac{{\cos {\theta _{ij}}}}{2}}&{\frac{{\sin \theta }}{2}{\theta _{ij}}}\\ { - \frac{3}{{2{l_{ij}}}}}&{\frac{{\sin {\theta _{ij}}}}{4}}&{ - \frac{{\cos {\theta _{ij}}}}{4}}&{\frac{3}{{2{l_{ij}}}}}&{\frac{{\sin {\theta _{ij}}}}{4}}&{ - \frac{{\cos {\theta _{ij}}}}{4}} \end{bmatrix} \begin{bmatrix} {{w_i}}&{{\varphi _{xi}}}&{{\varphi _{yi}}}&{{w_j}}&{{\varphi _{xj}}}&{{\varphi _{yj}}} \end{bmatrix}^T \quad{(8)} [cosθij−sinθijsinθijcosθij][φxkφyk]=[0−2lij32cosθij4sinθij2sinθij−4cosθij02lij32cosθij4sinθij2sinθθij−4cosθij][wiφxiφyiwjφxjφyj]T(8)
至此可以得到中点 k k k的转动变量端点 i j ij ij转动变量得关系: [ φ x k φ y k ] = [ 3 sin θ i j 2 l i j 2 cos 2 θ i j − sin 2 θ i j 4 3 sin θ i j cos θ i j 4 − 3 sin θ i j 2 l i j 2 cos 2 θ i j − sin 2 θ i j 4 3 sin θ i j cos θ i j 4 − 3 cos θ i j 2 l i j 3 sin θ i j cos θ i j 4 2 sin 2 θ i j − cos 2 θ i j 4 3 cos θ i j 2 l i j 3 sin θ i j cos θ i j 4 2 sin 2 θ i j − cos 2 θ i j 4 ] [ w i φ x i φ y i w j φ x j φ y j ] T ( 9 ) \begin{bmatrix} {{\varphi _{xk}}}\\ {{\varphi _{yk}}} \end{bmatrix} = \begin{bmatrix} {\frac{{3\sin {\theta _{ij}}}}{{2{l_{ij}}}}}&{\frac{{2{{\cos }^2}{\theta _{ij}} - {{\sin }^2}{\theta _{ij}}}}{4}}&{\frac{{3\sin {\theta _{ij}}\cos {\theta _{ij}}}}{4}}&{ - \frac{{3\sin {\theta _{ij}}}}{{2{l_{ij}}}}}&{\frac{{2{{\cos }^2}{\theta _{ij}} - {{\sin }^2}{\theta _{ij}}}}{4}}&{\frac{{3\sin {\theta _{ij}}\cos {\theta _{ij}}}}{4}}\\ { - \frac{{3\cos {\theta _{ij}}}}{{2{l_{ij}}}}}&{\frac{{3\sin {\theta _{ij}}\cos {\theta _{ij}}}}{4}}&{\frac{{2{{\sin }^2}{\theta _{ij}} - {{\cos }^2}{\theta _{ij}}}}{4}}&{\frac{{3\cos {\theta _{ij}}}}{{2{l_{ij}}}}}&{\frac{{3\sin {\theta _{ij}}\cos {\theta _{ij}}}}{4}}&{\frac{{2{{\sin }^2}{\theta _{ij}} - {{\cos }^2}{\theta _{ij}}}}{4}} \end{bmatrix} \begin{bmatrix} {{w_i}}&{{\varphi _{xi}}}&{{\varphi _{yi}}}&{{w_j}}&{{\varphi _{xj}}}&{{\varphi _{yj}}} \end{bmatrix}^T \quad{(9)} [φxkφyk]=⎣⎡2lij3sinθij−2lij3cosθij42cos2θij−sin2θij43sinθijcosθij43sinθijcosθij42sin2θij−cos2θij−2lij3sinθij2lij3cosθij42cos2θij−sin2θij43sinθijcosθij43sinθijcosθij42sin2θij−cos2θij⎦⎤[wiφxiφyiwjφxjφyj]T(9)
根据式(9),可以分别求得三个中点的转动变量得变换表达式,同时若令 x i j = x j − x i , y i j = y j − y i x_{ij}=x_j-x_i,y_{ij}=y_j-y_i xij=xj−xi,yij=yj−yi,则 sin θ i j = − x i j / l i j , cos θ i j = y i j / l i j \sin \theta_{ij}=-{x_ij}/l_{ij},\cos \theta_{ij}=y_{ij}/l_{ij} sinθij=−xij/lij,cosθij=yij/lij。所以又可以得到如下的关系: [ φ x 4 φ y 4 φ x 5 φ y 5 φ x 6 φ y 6 ] T = c o e f ∙ a (10) \begin{bmatrix} {{\varphi _{x4}}}&{{\varphi _{y4}}}&{{\varphi _{x5}}}&{{\varphi _{y5}}}&{{\varphi _{x6}}}&{{\varphi _{y6}}} \end{bmatrix} ^T= {\bf{coef}} \bullet {\bf{a}} \tag{10} [φx4φy4φx5φy5φx6φy6]T=coef∙a(10)
式中, a = [ w 1 φ x 1 φ y 1 w 2 φ x 2 φ y 2 w 3 φ x 3 φ y 3 ] T {\bf{a}} = \begin{bmatrix} {{w_1}}&{{\varphi _{x1}}}&{{\varphi _{y1}}}&{{w_2}}&{{\varphi _{x2}}}&{{\varphi _{y2}}}&{{w_3}}&{{\varphi _{x3}}}&{{\varphi _{y3}}} \end{bmatrix} ^T a=[w1φx1φy1w2φx2φy2w3φx3φy3]T
c o e f = [ − 3 x 12 2 l 12 2 2 y 12 2 − x 12 2 4 l 12 2 − 3 x 12 y 12 4 l 12 2 3 x 12 2 l 12 2 2 y 12 2 − x 12 2 4 l 12 2 − 3 x 12 y 12 4 l 12 2 0 0 0 − 3 y 12 2 l 12 2 − 3 x 12 y 12 4 l 12 2 2 x 12 2 − y 12 2 4 l 12 2 3 y 12 2 l 12 2 − 3 x 12 y 12 4 l 12 2 2 x 12 2 − y 12 2 4 l 12 2 0 0 0 0 0 0 − 3 x 23 2 l 23 2 2 y 23 2 − x 23 2 4 l 23 2 − 3 x 23 y 23 4 l 23 2 3 x 23 2 l 23 2 2 y 23 2 − x 23 2 4 l 23 2 − 3 x 23 y 23 4 l 23 2 0 0 0 − 3 y 23 2 l 23 2 − 3 x 23 y 23 4 l 23 2 2 x 23 2 − y 23 2 4 l 23 2 3 x 23 2 l 23 2 − 3 x 23 y 23 4 l 23 2 2 x 23 2 − y 23 2 4 l 23 2 3 x 31 2 l 31 2 2 y 31 2 − x 31 2 4 l 31 2 − 3 x 31 y 31 4 l 31 2 0 0 0 − 3 x 31 2 l 31 2 2 y 31 2 − x 31 2 4 l 31 2 − 3 x 31 y 31 4 l 31 2 3 y 31 2 l 31 2 − 3 x 31 y 31 4 l 31 2 2 x 31 2 − y 31 2 4 l 31 2 0 0 0 − 3 y 31 2 l 31 2 − 3 x 31 y 31 4 l 31 2 2 x 31 2 − y 31 2 4 l 31 2 ] \bf{coef}= \begin{bmatrix} { - \frac{{3{x_{12}}}}{{2l_{12}^2}}}&{\frac{{2y_{12}^2 - x_{12}^2}}{{4l_{12}^2}}}&{ - \frac{{3{x_{12}}{y_{12}}}}{{4l_{12}^2}}}&{\frac{{3{x_{12}}}}{{2l_{12}^2}}}&{\frac{{2y_{12}^2 - x_{12}^2}}{{4l_{12}^2}}}&{ - \frac{{3{x_{12}}{y_{12}}}}{{4l_{12}^2}}}&0&0&0\\ { - \frac{{3{y_{12}}}}{{2l_{12}^2}}}&{ - \frac{{3{x_{12}}{y_{12}}}}{{4l_{12}^2}}}&{\frac{{2x_{12}^2 - y_{12}^2}}{{4l_{12}^2}}}&{\frac{{3{y_{12}}}}{{2l_{12}^2}}}&{ - \frac{{3{x_{12}}{y_{12}}}}{{4l_{12}^2}}}&{\frac{{2x_{12}^2 - y_{12}^2}}{{4l_{12}^2}}}&0&0&0\\ 0&0&0&{ - \frac{{3{x_{23}}}}{{2l_{23}^2}}}&{\frac{{2y_{23}^2 - x_{23}^2}}{{4l_{23}^2}}}&{ - \frac{{3{x_{23}}{y_{23}}}}{{4l_{23}^2}}}&{\frac{{3{x_{23}}}}{{2l_{23}^2}}}&{\frac{{2y_{23}^2 - x_{23}^2}}{{4l_{23}^2}}}&{ - \frac{{3{x_{23}}{y_{23}}}}{{4l_{23}^2}}}\\ 0&0&0&{ - \frac{{3{y_{23}}}}{{2l_{23}^2}}}&{ - \frac{{3{x_{23}}{y_{23}}}}{{4l_{23}^2}}}&{\frac{{2x_{23}^2 - y_{23}^2}}{{4l_{23}^2}}}&{\frac{{3{x_{23}}}}{{2l_{23}^2}}}&{ - \frac{{3{x_{23}}{y_{23}}}}{{4l_{23}^2}}}&{\frac{{2x_{23}^2 - y_{23}^2}}{{4l_{23}^2}}}\\ {\frac{{3{x_{31}}}}{{2l_{31}^2}}}&{\frac{{2y_{31}^2 - x_{31}^2}}{{4l_{31}^2}}}&{ - \frac{{3{x_{31}}{y_{31}}}}{{4l_{31}^2}}}&0&0&0&{ - \frac{{3{x_{31}}}}{{2l_{31}^2}}}&{\frac{{2y_{31}^2 - x_{31}^2}}{{4l_{31}^2}}}&{ - \frac{{3{x_{31}}{y_{31}}}}{{4l_{31}^2}}}\\ {\frac{{3{y_{31}}}}{{2l_{31}^2}}}&{ - \frac{{3{x_{31}}{y_{31}}}}{{4l_{31}^2}}}&{\frac{{2x_{31}^2 - y_{31}^2}}{{4l_{31}^2}}}&0&0&0&{ - \frac{{3{y_{31}}}}{{2l_{31}^2}}}&{ - \frac{{3{x_{31}}{y_{31}}}}{{4l_{31}^2}}}&{\frac{{2x_{31}^2 - y_{31}^2}}{{4l_{31}^2}}} \end{bmatrix} coef=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡−2l1223x12−2l1223y12002l3123x312l3123y314l1222y122−x122−4l1223x12y12004l3122y312−x312−4l3123x31y31−4l1223x12y124l1222x122−y12200−4l3123x31y314l3122x312−y3122l1223x122l1223y12−2l2323x23−2l2323y23004l1222y122−x122−4l1223x12y124l2322y232−x232−4l2323x23y2300−4l1223x12y124l1222x122−y122−4l2323x23y234l2322x232−y23200002l2323x232l2323x23−2l3123x31−2l3123y31004l2322y232−x232−4l2323x23y234l3122y312−x312−4l3123x31y3100−4l2323x23y234l2322x232−y232−4l3123x31y314l3122x312−y312⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
根据式(2)和(10)得到单元内任意点的插值函数表达式为:
[ φ x φ y ] T = ( N 1 + N 2 ∙ c o e f ) a (11) \begin{bmatrix} {{\varphi _{x}}} & {{\varphi _{y}}} \end{bmatrix} ^T = (\bf{N_1}+\bf{N_2} \bullet\bf{coef})\bf{a} \tag{11} [φxφy]T=(N1+N2∙coef)a(11)
式中,
N 1 = [ 0 N 1 0 0 N 2 0 0 N 3 0 0 0 N 1 0 0 N 2 0 0 N 3 ] \bf{N_1}=\begin{bmatrix} 0&{{N_1}}&0&0&{{N_2}}&0&0&{{N_3}}&0\\ 0&0&{{N_1}}&0&0&{{N_2}}&0&0&{{N_3}} \end{bmatrix} N1=[00N100N100N200N200N300N3] N 2 = [ N 4 0 N 5 0 N 6 0 0 N 4 0 N 5 0 N 6 ] \bf{N_2} = \begin{bmatrix} {{N_4}}&0&{{N_5}}&0&{{N_6}}&0\\ 0&{{N_4}}&0&{{N_5}}&0&{{N_6}} \end{bmatrix} N2=[N400N4N500N5N600N6]
上述推导中,转动变量 φ x , φ y \varphi _{x}, \varphi _{y} φx,φy的方向和坐标轴正向并不一致,若想一致,可以参考文献[2],这样求得的系数矩阵 c o e f \bf{coef} coef会有所不同。插值函数表达成式(11),有利于推导和程序的实现。
单元刚度矩阵
Kirchhoff板的几何方程为:
ε κ = − z [ φ x ∂ x φ y ∂ y φ x ∂ y + φ y ∂ x ] T (12) \varepsilon _\kappa=-z\begin{bmatrix} {\frac{{{\varphi _{x}}}}{{\partial x}}} & {\frac{{{\varphi _{y}}}}{{\partial y}}} & {\frac{{{\varphi _{x}}}}{{\partial y}}} +{\frac{{{\varphi _{y}}}}{{\partial x}}} \end{bmatrix}^T \tag{12} εκ=−z[∂xφx∂yφy∂yφx+∂xφy]T(12)
将式(10)代入几何方程,得:
ε κ = − z ( B 1 + B 2 ∙ c o e f ) a (13) \varepsilon _\kappa=-z(\bf{B_1}+\bf{B_2}\bullet\bf{coef})\bf{a} \tag{13} εκ=−z(B1+B2∙coef)a(13)
式中,
B 1 = [ 0 ∂ N 1 ∂ x 0 0 ∂ N 2 ∂ x 0 0 ∂ N 3 ∂ x 0 0 0 ∂ N 1 ∂ y 0 0 ∂ N 2 ∂ y 0 0 ∂ N 3 ∂ y 0 ∂ N 1 ∂ y ∂ N 1 ∂ x 0 ∂ N 2 ∂ y ∂ N 2 ∂ x 0 ∂ N 3 ∂ y ∂ N 3 ∂ x ] {{\bf{B}}_{\bf{1}}}=\begin{bmatrix} 0&{\frac{{\partial {N_1}}}{{\partial x}}}&0&0&{\frac{{\partial {N_2}}}{{\partial x}}}&0&0&{\frac{{\partial {N_3}}}{{\partial x}}}&0\\ 0&0&{\frac{{\partial {N_1}}}{{\partial y}}}&0&0&{\frac{{\partial {N_2}}}{{\partial y}}}&0&0&{\frac{{\partial {N_3}}}{{\partial y}}}\\ 0&{\frac{{\partial {N_1}}}{{\partial y}}}&{\frac{{\partial {N_1}}}{{\partial x}}}&0&{\frac{{\partial {N_2}}}{{\partial y}}}&{\frac{{\partial {N_2}}}{{\partial x}}}&0&{\frac{{\partial {N_3}}}{{\partial y}}}&{\frac{{\partial {N_3}}}{{\partial x}}} \end{bmatrix} B1=⎣⎢⎡000∂x∂N10∂y∂N10∂y∂N1∂x∂N1000∂x∂N20∂y∂N20∂y∂N2∂x∂N2000∂x∂N30∂y∂N30∂y∂N3∂x∂N3⎦⎥⎤
B 2 = [ ∂ N 4 ∂ x 0 ∂ N 5 ∂ x 0 ∂ N 6 ∂ x 0 0 ∂ N 4 ∂ y 0 ∂ N 5 ∂ y 0 ∂ N 6 ∂ y ∂ N 4 ∂ y ∂ N 4 ∂ x ∂ N 5 ∂ y ∂ N 5 ∂ x ∂ N 6 ∂ y ∂ N 6 ∂ x ] {{\bf{B}}_2}{\rm{ = }}\begin{bmatrix} {\frac{{\partial {N_4}}}{{\partial x}}}&0&{\frac{{\partial {N_5}}}{{\partial x}}}&0&{\frac{{\partial {N_6}}}{{\partial x}}}&0\\ 0&{\frac{{\partial {N_4}}}{{\partial y}}}&0&{\frac{{\partial {N_5}}}{{\partial y}}}&0&{\frac{{\partial {N_6}}}{{\partial y}}}\\ {\frac{{\partial {N_4}}}{{\partial y}}}&{\frac{{\partial {N_4}}}{{\partial x}}}&{\frac{{\partial {N_5}}}{{\partial y}}}&{\frac{{\partial {N_5}}}{{\partial x}}}&{\frac{{\partial {N_6}}}{{\partial y}}}&{\frac{{\partial {N_6}}}{{\partial x}}} \end{bmatrix} B2=⎣⎢⎡∂x∂N40∂y∂N40∂y∂N4∂x∂N4∂x∂N50∂y∂N50∂y∂N5∂x∂N5∂x∂N60∂y∂N60∂y∂N6∂x∂N6⎦⎥⎤
单元刚度矩阵为:
K = ∫ ( B 1 + B 2 ∙ c o e f ) T D ( B 1 + B 2 ∙ c o e f ) d x d y (14) {\bf{K}}{\rm{ = }}\int {{{\left( {{{\bf{B}}_{\bf{1}}} + {{\bf{B}}_{\bf{2}}} \bullet {\bf{coef}}} \right)}^T}{\bf{D}}\left( {{{\bf{B}}_{\bf{1}}} + {{\bf{B}}_{\bf{2}}} \bullet {\bf{coef}}} \right)dxdy} \tag{14} K=∫(B1+B2∙coef)TD(B1+B2∙coef)dxdy(14)
式中,矩阵D为:
D = E h 3 12 ( 1 − ν 2 ) [ 1 ν 0 ν 1 0 0 0 1 − ν 2 ] {\bf{D}}{\rm{ = }}\frac{{E{h^3}}}{{12\left( 1-\nu ^2 \right)}} \begin{bmatrix} 1&\nu &0\\ \nu &1&0\\ 0&0&\frac{1-\nu}{2} \end{bmatrix} D=12(1−ν2)Eh3⎣⎡1ν0ν100021−ν⎦⎤
对式(14)进行换元,转换到面积坐标 ( L 1 , L 2 ) (\bf{L_1},\bf{L_2}) (L1,L2)下求积分:
K = ∫ 0 1 ∫ 0 1 − L 2 ( B 1 + B 2 ∙ c o e f ) T D ( B 1 + B 2 ∙ c o e f ) ∣ J ∣ d L 1 d L 2 (15) \bf{K}= \int_0^1 {\int_0^{1 - L_2}} {{\left( {{{\bf{B}}_{\bf{1}}} + {{\bf{B}}_{\bf{2}}} \bullet {\bf{coef}}} \right)}^T}{\bf{D}\left( {{{\bf{B}}_{\bf{1}}} + {{\bf{B}}_{\bf{2}}} \bullet {\bf{coef}}} \right)\left| {\bf{J}} \right|d{L_1}d{L_2}} \tag{15} K=∫01∫01−L2(B1+B2∙coef)TD(B1+B2∙coef)∣J∣dL1dL2(15)
整体坐标和面积坐标的关系:
x = ∑ i = 1 3 L i x i , y = ∑ i = 1 3 L i y i (16) {x}=\sum_{i=1}^{3} L_{i} {x_i}, {y}=\sum_{i=1}^{3} L_{i} {y_i} \tag{16} x=i=1∑3Lixi,y=i=1∑3Liyi(16)
所以雅克比矩阵 J \bf{J} J为:
J = [ ∂ x ∂ L 1 ∂ y ∂ L 1 ∂ x ∂ L 2 ∂ y ∂ L 2 ] = [ 1 0 − 1 0 1 − 1 ] [ x 1 y 1 x 2 y 2 x 3 y 3 ] (17) {\bf{J}} = \begin{bmatrix} {\frac{{\partial x}}{{\partial {L_1}}}}&{\frac{{\partial y}}{{\partial {L_1}}}}\\ {\frac{{\partial x}}{{\partial {L_2}}}}&{\frac{{\partial y}}{{\partial {L_2}}}}\end{bmatrix} =\begin{bmatrix} 1&0&{ - 1}\\ 0&1&{ - 1} \end{bmatrix}\begin{bmatrix} {{x_1}}&{{y_1}}\\ {{x_2}}&{{y_2}}\\ {{x_3}}&{{y_3}} \end{bmatrix} \tag{17} J=[∂L1∂x∂L2∂x∂L1∂y∂L2∂y]=[1001−1−1]⎣⎡x1x2x3y1y2y3⎦⎤(17)
插值函数 N i {N_i} Ni由面积坐标表示为:
{ N i = ( 2 L i − 1 ) L i i = 1 , 2 , 3 N k = 4 L i L j k = 4 , 5 , 6 , 为 i j 的 中 点 (18) \left\{\begin{array}{l} N_i=(2L_i - 1)L_i & i = 1,2,3\\ N_k = 4L_iL_j & {k = 4,5,6,为ij的中点} \end{array}\right. \tag{18} {Ni=(2Li−1)LiNk=4LiLji=1,2,3k=4,5,6,为ij的中点(18)
根据链式求导法则,函数对于 x , y x,y x,y的偏导均可以转换为对面积坐标的偏导:
[ ∂ ∂ x ∂ ∂ y ] = 1 2 A [ b 1 b 2 b 3 c 1 c 2 c 3 ] [ ∂ ∂ L 1 ∂ ∂ L 2 ∂ ∂ L 3 ] T (19) \begin{bmatrix} {\frac{\partial }{{\partial x}}}\\ {\frac{\partial }{{\partial y}}} \end{bmatrix}{\rm{ = }}\frac{1}{{2A}}\begin{bmatrix} {{b_1}}&{{b_2}}&{{b_3}}\\ {{c_1}}&{{c_2}}&{{c_3}} \end{bmatrix} \begin{bmatrix} {\frac{\partial }{{\partial {L_1}}}}&{\frac{\partial }{{\partial {L_2}}}}&{\frac{\partial }{{\partial {L_3}}}} \end{bmatrix}^T \tag{19} [∂x∂∂y∂]=2A1[b1c1b2c2b3c3][∂L1∂∂L2∂∂L3∂]T(19)
由式(18)和(19)就可以求得插值函数对 x , y x,y x,y的偏导,至此单元刚度矩阵就可求得。关于面积坐标的内容可以查阅参考书籍[1]。
算例
四边简支薄板受均布荷载,板尺寸为 a = b = 1 m , h = 0.01 m a=b=1m,h=0.01m a=b=1m,h=0.01m,弹性模量 E = 7 e 7 E=7e7 E=7e7,泊松比 ν = 0.3 \nu=0.3 ν=0.3,均布荷载 f = 1 P a f=1Pa f=1Pa。
(1) 挠度云图

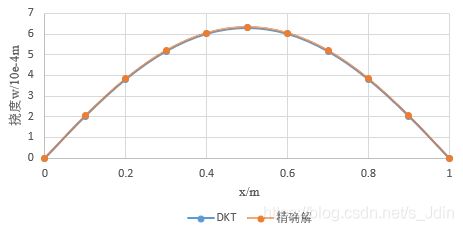
(2)中线挠度对比
收藏点赞本文,私信博主获取算例Matlab代码。码字不易,感谢支持。
参考文献:
[1] 王勖成. 有限单元法[M]. 清华大学出版社, 2003.
[2] Batoz J L, Bathe K, Ho L W. A Study of three-node triangular bending elements[J]. International Journal for Numerical Methods in Engineering, 1980,15(12):1771-1812.