PyTorch深度学习实践概论笔记7-处理多维特征的输入

上一讲PyTorch深度学习实践概论笔记6-逻辑斯蒂回归中讨论了用Logistic回归实现二分类问题。之前面对的都是单维数据，接下来讨论当我们面对多维数据时如何处理。单维指输入x是一个实数；多维输入指x有多个不同的特征，预测对应的分类。这一讲是处理多维特征的输入。

0 Revison

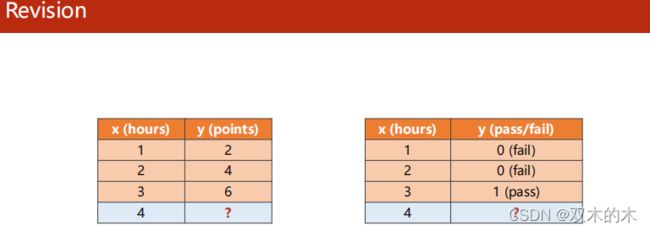
之前用到的数据集：

• 左侧：回归，输出y属于实数
• 右侧：分类，输出y属于离散集合

1 Diabetes Dataset

接下来看一个糖尿病的数据集，是一个分类问题。

对于上面这个数据集，在机器学习中每一行叫做一个样本，每一列叫做一个特征。在数据库中，每一行叫做一个记录，每一列叫做一个字段。

2 Multiple Dimension Logistic Regression Model

在机器学习和数据库中处理数据的方式略有不同。在机器学习里面，拿到数据表之后，把内容分成两部分，一部分作为输入x，另一部分作为输入y。如果训练是从数据库读数据，就把x读出来构成一个矩阵，把y字段读出来构成一个矩阵，就把输入的数据集准备好了。

如下图：Anaconda的安装目录下已经给我们准备好了一些数据集，gz是linux下非常流行的压缩格式。

单个维度特征输入时，x是一个实数，乘上一个权重w就可以了。现在x变成了8个维度，每一个特征值xi都要与一个w相乘，这样能算出一个实数。

2.1 Mini-Batch(N samples)

注意：pytorch提供的sigmoid函数是按向量计算的形式。（numpy有专门向量化的方法，推荐tfidf）处理成向量形式可以使用并行运算，提供运算的效率。

代码分析：

class Model(torch.nn.Module):

    def __init__(self):

    	super(Model, self).__init__()

    	self.linear = torch.nn.Linear(8, 1)#线性层：输入8维，输出1维

    	self.sigmoid = torch.nn.Sigmoid()
    

    def forward(self, x):

    	x = self.sigmoid(self.linear(x))

    	return x

model = Model()

2.1.1 Linear Layer

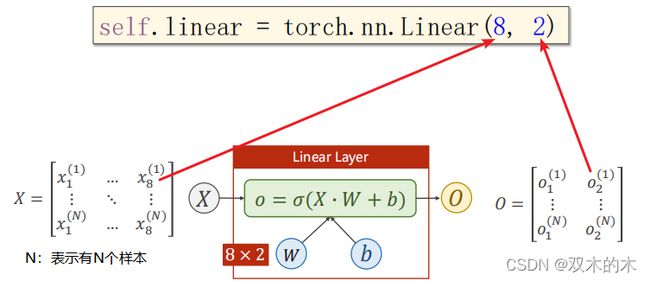
下面具体分析一下线性层：

上面X的列数对应feature，行数对应N个样本。 上面是输出为1维的情况。接下来看看输出2维的情况：

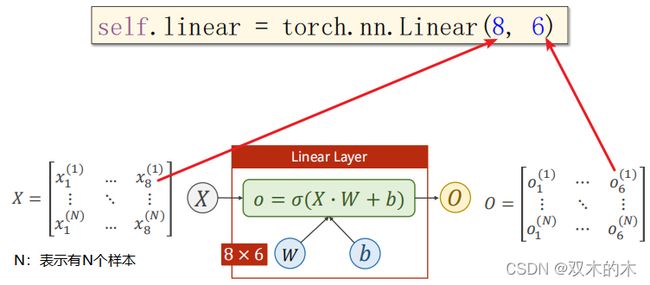
将矩阵的乘法运算看成空间变换的函数，可以看做从N维空间映射到M维空间的线性变换。 上述（8,2）线性层就是把一个8D空间映射到2D空间。同理，也可以把8D空间降到6D空间：

2.1.2 Neural Network

把多个类似于logistic回归的线性变换单元首尾相连，构造多层神经网络。网络可以降维，同样也可以升维。神经网络到底多少层，每层多少维，这要看具体的网络构成，需要用超参数搜索的方法进行尝试，看什么样的设计在开发集表现更好。好的网络不仅要有好的学习能力，也要有好的泛化能力。老师类比于大学的课程，不同过去的“扣书本”，而是掌握“读文档，基本架构理念”的能力，这种能力泛化能力比较好（以后如果换了编程语言，也可以很快上手）。

3 Example

3.1 Example1: Artificial Neural Network

神经网络的本质：寻找一种非线性的空间变换函数。

3.2 Example2: Diabetes Prediction

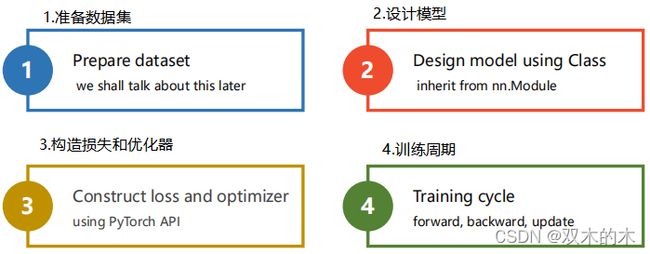
回忆之前的步骤：

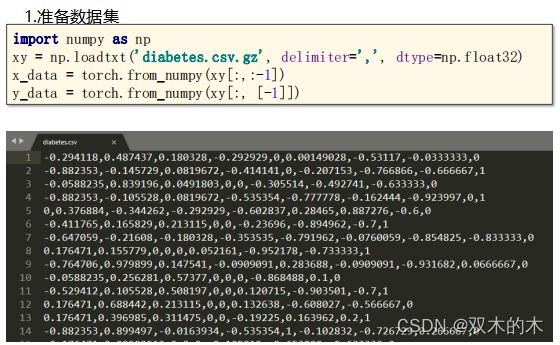
3.2.1 Example: 1.Prepare Dataset

代码分析：

import numpy as np

#第一个参数是数据集的路径，第二个参数是数据的分割方式，第三个参数是数据类型
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)

x_data = torch.from_numpy(xy[:,:-1])

y_data = torch.from_numpy(xy[:, [-1]])  #[-1]保证拿出来的是矩阵，不加[]拿出来的是向量

关于读取数据的数据类型，为什么不用double呢？在神经网络里通常使用32浮点数，这和显卡有关。一般一点的显卡不支持double类型的数据，像1080和2080。

3.2.2 Example: 2.Define Model

代码分析：

import torch


class Model(torch.nn.Module):

    def __init__(self):

    	super(Model, self).__init__()

    	self.linear1 = torch.nn.Linear(8, 6)

    	self.linear2 = torch.nn.Linear(6, 4)

    	self.linear3 = torch.nn.Linear(4, 1)

    	self.sigmoid = torch.nn.Sigmoid() #torch.nn.Sigmoid()是一个模块，继承于nn.Module
     

    def forward(self, x):
        #序列式的模型为了不乱：建议从头到尾用一个变量x

    	x = self.sigmoid(self.linear1(x))

    	x = self.sigmoid(self.linear2(x))

    	x = self.sigmoid(self.linear3(x))

    	return x
     

model = Model()

3.2.3 Example: 3.Construct Loss and Optimizer

代码分析：

criterion = torch.nn.BCELoss(size_average=True)

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

3.2.4 Example: 4.Training Cycle

代码分析：

for epoch in range(100):

    # Forward

    y_pred = model(x_data)

    loss = criterion(y_pred, y_data)

    print(epoch, loss.item())
    

    # Backward

    optimizer.zero_grad()

    loss.backward()
    

    # Update

    optimizer.step()

输出结果如下（个位数为9的epoch才输出）：

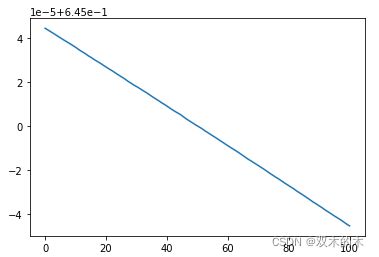
画一下loss的图像：

因为数据集中在0.645附近，所以调整了y轴的刻度。 

4 Exercise: Try different activate function

练习：尝试不同的激活函数。

上述ref:http://rasbt.github.io/mlxtend/user_guide/general_concepts/activation-functions/#activation-functions-for-artificial-neural-networks

在神经网络中使用较多的ReLu激活函数：

上述激活函数可视化链接:https://dashee87.github.io/data%20science/deep%20learning/visualising-activation-functions-in-neural-networks/

ref：torch.nn — PyTorch 1.10.1 documentation

刘老师推荐代码如下：

import torch


class Model(torch.nn.Module):

    def __init__(self):

    	super(Model, self).__init__()

    	self.linear1 = torch.nn.Linear(8, 6)

    	self.linear2 = torch.nn.Linear(6, 4)

    	self.linear3 = torch.nn.Linear(4, 1)

    	self.activate = torch.nn.ReLU()#使用ReLU激活函数
     

    def forward(self, x):

    	x = self.activate(self.linear1(x))

    	x = self.activate(self.linear2(x))

    	x = self.activate(self.linear3(x))  #最后在算y hat时，激活函数建议改成sigmiod函数

    	return x
     

model = Model()

【我的解答】使用ReLU+sigmoid激活函数组合。

代码如下：

import numpy as np
import torch

xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype=np.float32)

x_data = torch.from_numpy(xy[:,:-1])

y_data = torch.from_numpy(xy[:, [-1]])


#修改激活函数为ReLU
class Model(torch.nn.Module):

    def __init__(self):
        
        super(Model, self).__init__()
        
        self.linear1 = torch.nn.Linear(8, 6)
        
        self.linear2 = torch.nn.Linear(6, 4)
        
        self.linear3 = torch.nn.Linear(4, 1)
        
        self.activate = torch.nn.ReLU()
        
        self.sigmoid = torch.nn.Sigmoid()
     

    def forward(self, x):

    	x = self.activate(self.linear1(x))

    	x = self.activate(self.linear2(x))

    	x = self.sigmoid(self.linear3(x))

    	return x
     

model = Model()


criterion = torch.nn.BCELoss(size_average=True)

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)


loss_list_ReLU = []
for epoch in range(100):

    # Forward

    y_pred = model(x_data)

    loss = criterion(y_pred, y_data)
    
    loss_list_ReLU.append(loss.item())
    
    if epoch%10==9:
        print(epoch, loss.item())
    

    # Backward

    optimizer.zero_grad()

    loss.backward()
    

    # Update

    optimizer.step()

输出结果：

 画出损失的对比图像：

import matplotlib.pyplot as plt

plt.plot(np.linspace(0,100,100),loss_list,color='red',label='loss_sigmoid')
plt.plot(np.linspace(0,100,100),loss_list_ReLU,color = 'green',label='loss_ReLU')
plt.legend()
plt.show()

可以看到只使用sigmoid激活函数得到的loss图像趋于平稳，使用ReLU+sigmoid(最后输出y hat)激活函数可以明显看到loss的下降。

由于最后两条曲线类似重合，为了进一步观察差异，迭代200次，得到图像如下：

上图表明只使用sigmoid激活函数的loss在50次迭代之后几乎不下降，而使用ReLU+sigmoid(最后输出y hat)激活函数loss有明显的下降趋势，模型训练效果更好（如果增加迭代次数，模型的训练效果可能更好）。

说明：记录学习笔记，如果错误欢迎指正！写文章不易，转载请联系我。