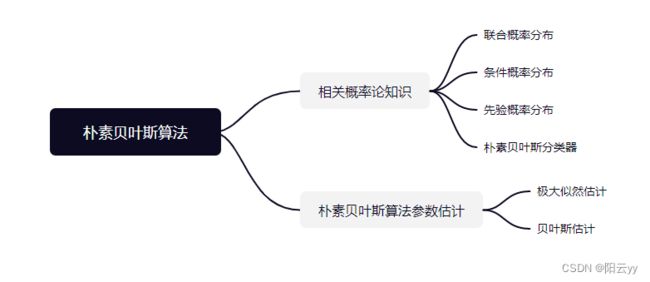
朴素贝叶斯算法原理以及python实现
朴素贝叶斯
- 一、朴素贝叶斯概述
- 二、概率论知识
- 三、朴素贝叶斯算法原理
- 四、参数估计方法
- 五、示例分析
- 六、拉普拉斯平滑修正
- 七、算法优缺点
- 八、python实现
-
- 8.1 sklearn贝叶斯
- 8.2 文本情感分析示例
- 8.3 CountVectorizer()函数
一、朴素贝叶斯概述
朴素贝叶斯算法(Naive Bayesian algorithm) 是应用最为广泛的分类算法之一。
朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重,也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布(朴素贝叶斯法这种通过学习得到模型的机制,显然属于生成模型);然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
二、概率论知识
- 条件概率:就是事件 A A A 在另外一个事件 B B B 已经发生条件下的发生概率。条件概率表示为 P ( A ∣ B ) P(A \mid B) P(A∣B) ,读作在 B B B 发生的条件下 A A A 发生的概率"。
- 联合概率: 表示两个事件共同发生 (数学概念上的交集) 的概率。 A A A 与 B B B 的联合概率表示为联合概率 P ( A B ) P(A B) P(AB)
P ( A B ) = P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) P(AB)=P(A \mid B) P(B)=P(B \mid A) P(A) P(AB)=P(A∣B)P(B)=P(B∣A)P(A)
若 A A A与 B B B独立
P ( A B ) = P ( A ) P ( B ) P(A B)=P(A) P(B) P(AB)=P(A)P(B) - 全概率公式: P ( X ) = ∑ k P ( X ∣ Y = Y k ) P ( Y k ) P(X)=\sum_{k} P\left(X \mid Y=Y_{k}\right) P\left(Y_{k}\right) P(X)=∑kP(X∣Y=Yk)P(Yk), 其中 ∑ k P ( Y k ) = 1 \sum_{k} P\left(Y_{k}\right)=1 ∑kP(Yk)=1
贝叶斯公式推导示例 :
已知某学校学生总人数为U,其中男生 : 60 % 60 \% 60%,女生 : 40 % 40 \% 40%
男生总是穿长裤, 女生则一半穿长裤一半穿裙子
正向概率: 随机选取一个学生, 他 (她) 穿长裤的概率和穿裙子的概率是多大
逆向概率: 迎面走来一个穿长裤的学生, 你只看得见他 (她) 穿的是否长裤, 而无法确定他 (她) 的性别, 你能够推断出他(她)是女生的概率是多大吗?
穿长裤的(男生): U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) U * P( Boy) * P (Pants \mid Boy) U∗P(Boy)∗P(Pants∣Boy)
P ( \mathrm{P}( P( Boy) 是男生的概率 = 60 % =60 \% =60%
P \mathrm{P} P (Pants|Boy) 是条件概率, 即在 Boy 这个条件下穿长裤的概 率是多大, 这里是 100 % 100 \% 100%, 因为所有男生都穿长裤
穿长裤的(女生) : U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) U * P(Girl) *P( Pants \mid Girl) U∗P(Girl)∗P(Pants∣Girl)
求解: 穿长裤的人里面有多少女生
穿长裤总数: U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) U * P( Boy ) * P(Pants \mid Boy )+U * P( Girl ) * P( Pants \mid Girl ) U∗P(Boy)∗P(Pants∣Boy)+U∗P(Girl)∗P(Pants∣Girl)
P ( G i r l ∣ P a n t s ) = U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) / P( Girl|Pants )=U * P(G i r l) * P( Pants \mid Girl ) / P(Girl∣Pants)=U∗P(Girl)∗P(Pants∣Girl)/ 穿长裤总数
U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) / [ U ∗ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + U ∗ P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) ] U^{*} P( Girl ) * P( Pants \mid Girl ) /[U * P( Boy ) * P( Pants \mid Boy )+U * P( Girl ) * P( Pants \mid Girl )] U∗P(Girl)∗P(Pants∣Girl)/[U∗P(Boy)∗P(Pants∣Boy)+U∗P(Girl)∗P(Pants∣Girl)]
= P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) / [ P ( B o y ) ∗ P ( P a n t s ∣ B o y ) + P ( G i r l ) ∗ P ( P a n t s ∣ G i r l ) ] = P( Girl ) * P( Pants \mid Girl ) /[ P( Boy ) * P( Pants \mid Boy )+P( Girl ) * P( Pants \mid Girl )] =P(Girl)∗P(Pants∣Girl)/[P(Boy)∗P(Pants∣Boy)+P(Girl)∗P(Pants∣Girl)]
可以发现最终结果与总人数无关。
由以上示例可推导出贝叶斯公式,此公式将 P ( A ∣ B ) P(A|B) P(A∣B)与 P ( B ∣ A ) P(B|A) P(B∣A)联系起来。
贝叶斯定理:贝叶斯理论是以18世纪的一位神学家托马斯.贝叶斯(Thomas Bayes)命名。通常,事件A在事件B (发生) 的条件下的概率, 与事件B在事件A (发生) 的条件下的概率是不一样的。然而,这两者是有确是的关系的,贝叶斯定理就是这种关系的阵述。
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
- P ( A ) \mathrm{P}(\mathrm{A}) P(A) : 先验概率。先验概率(prior probability) 是指事情还没有发生,求这件事情发生的可能性的大小,是先验概率。它往往作 为"由因求果"问题中的"因"出顼。
- P ( A ∣ B ) \mathrm{P}(\mathrm{A} \mid \mathrm{B}) P(A∣B) : 后验概率。后验概率是指事情已经发生,求这件事情发生的原因是由某个因素引起的可能性的大小。后验概率的计算要 以先验概率为基础
- P ( B ∣ A ) \mathrm{P}(\mathrm{B} \mid \mathrm{A}) P(B∣A) : 条件概率,又叫似然概率,一般是通过历史数据统计得到。一般不把它叫做先验概率,但从定义上也符合先验定义。
三、朴素贝叶斯算法原理
朴素贝叶斯方法是其于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集,首先其于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对于给定的输入 x x x ,通过学习到的模型计算后验概率分布 P ( Y = c k ∣ X = P\left(Y=c_{k} \mid X=\right. P(Y=ck∣X= x x x ),将后验概率最大的类作为 x x x 的类输出。其中后验概率计算根据贝叶斯定理进行:
条件概率(条件独立):
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , … , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x j ∣ Y = c k ) P\left(X=x \mid Y=c_{k}\right)=P\left(X^{(1)=} x^{(1)}, \ldots, X^{(n)=} x^{(n)} \mid Y=c_{k}\right)=\prod_{j=1}^{n} P\left(X^{(j)}=x^{j} \mid Y=c_{k}\right) P(X=x∣Y=ck)=P(X(1)=x(1),…,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=xj∣Y=ck)
P ( Y = c k ∣ X = x ) = P ( X = x ∣ Y = c k ) P ( Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) P\left(Y=c_{k} \mid X=x\right)=\frac{P\left(X=x \mid Y=c_{k}\right) P\left(Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right)} P(Y=ck∣X=x)=∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(X=x∣Y=ck)P(Y=ck)
然后,最后的朴素贝叶斯分类模型为:
y = f ( x ) = arg max c k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = c k ) y=f(x)=\operatorname{arg \ max}_{c_{k}} \frac{P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right)}{\sum_{k} P\left(Y=c_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right)} y=f(x)=arg maxck∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)
针对贝叶斯定理,由于所有类别的全概 P ( x ) P(x) P(x)部分相同,那么
y = arg max c k P ( Y = c k ) ∏ j = 1 d P ( X ( j ) = x ( j ) ∣ Y = c k ) y=\operatorname{arg \ max}_{c_{k}}{P\left(Y=c_{k}\right) \prod_{j=1}^d P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right)} y=arg maxckP(Y=ck)j=1∏dP(X(j)=x(j)∣Y=ck)
四、参数估计方法
极大似然估计(Maximum Likelihood Estimation,MLE)和贝叶斯估计(Bayesian Estimation)是统计推断中两种最常用的参数估计方法。
- 极大似然估计
最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提 供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数末知"。通过若干次试验,观察其结果,利用试验 结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
由于样本集中的样本都是独立同分布,可以只考虑一类样本集 D D D,来估计参数向量 θ \theta θ 。记已知的样本集为:
D = { x 1 , x 2 , ⋯ , x N } D=\left\{x_{1}, x_{2}, \cdots, x_{N}\right\} D={x1,x2,⋯,xN}
似然函数 (linkehood function) : 联合概率密度函数 P ( D ∣ θ ) P(D \mid \theta) P(D∣θ),称为相对于 { x 1 , x 2 , ⋯ , x N } \left\{x_{1}, x_{2}, \cdots, x_{N}\right\} {x1,x2,⋯,xN}的 θ \theta θ 的似然函数。
l ( θ ) = P ( D ∣ θ ) = P ( x 1 ∣ θ ) P ( x 2 ∣ θ ) ⋯ P ( x n ∣ θ ) = ∏ i = 1 N P ( x i ∣ θ ) l(\theta)=P(D \mid \theta)=P(x_{1}\mid \theta)P(x_2\mid \theta)\cdots P(x_n\mid \theta)=\prod_{i=1}^{N} P\left(x_{i} \mid \theta\right) l(θ)=P(D∣θ)=P(x1∣θ)P(x2∣θ)⋯P(xn∣θ)=i=1∏NP(xi∣θ) 如果 θ ^ \hat{\theta} θ^ 是参数空间中能使似然函数 l ( θ ) l(\theta) l(θ) 最大的 θ \theta θ 值,则 θ ^ \hat{\theta} θ^ 应该是 “最可能” 的参数值,那么 θ ^ \hat{\theta} θ^ 就是 θ \theta θ 的极大似然估计量。它是样本集的函数,记作:
θ ^ = d ( x 1 , x 2 , ⋯ , x N ) = d ( D ) \hat{\theta}=d\left(x_{1}, x_{2}, \cdots, x_{N}\right)=d(D) θ^=d(x1,x2,⋯,xN)=d(D)
θ ^ ( x 1 , x 2 , ⋯ , x N ) \hat{\theta}\left(x_{1}, x_{2}, \cdots, x_{N}\right) θ^(x1,x2,⋯,xN) 称作极大似然函数估计值
求解极大似然函数
M L ML ML 估计:求使得出现该组样本的概率最大的 θ \theta θ 值。
θ ^ = arg max θ l ( θ ) = arg max θ ∏ i = 1 N P ( x i ∣ θ ) \hat{\theta}=\arg \max _{\theta} l(\theta)=\arg \max _{\theta} \prod_{i=1}^{N} P\left(x_{i} \mid \theta\right) θ^=argθmaxl(θ)=argθmaxi=1∏NP(xi∣θ)
实际中为了便于分析,定义了对数似然函数:
H ( θ ) = ln l ( θ ) θ ^ = arg max θ H ( θ ) = arg max θ ln l ( θ ) = arg max θ ∏ i = 1 N P ( x i ∣ θ ) \begin{gathered} H(\theta)=\ln l(\theta) \\ \hat{\theta}=\arg \max _{\theta} H(\theta)=\arg \max _{\theta} \ln l(\theta)=\arg \max _{\theta} \prod_{i=1}^{N} P\left(x_{i} \mid \theta\right) \end{gathered} H(θ)=lnl(θ)θ^=argθmaxH(θ)=argθmaxlnl(θ)=argθmaxi=1∏NP(xi∣θ)
末知参数只有一个 ( θ \theta θ 为标量 )
在似然函数满足连续、可微的正则条件下,极大似然估计量是下面微分方程的解:
d l ( θ ) d θ = 0 或者等价于 d H ( θ ) d θ = d ln l ( θ ) d θ = 0 \frac{d l(\theta)}{d \theta}=0 \text { 或者等价于 } \frac{d H(\theta)}{d \theta}=\frac{d \ln l(\theta)}{d \theta}=0 dθdl(θ)=0 或者等价于 dθdH(θ)=dθdlnl(θ)=0
末知参数有多个 ( θ \theta θ 为向量)
则 θ \theta θ 可表示为具有 S S S 个分量的末知向量:
θ = [ θ 1 , θ 2 , ⋯ , θ S ] T \theta=\left[\theta_{1}, \theta_{2}, \cdots, \theta_{S}\right]^{T} θ=[θ1,θ2,⋯,θS]T
记梯度:
∇ θ = [ ∂ ∂ θ 1 , ∂ ∂ θ 2 , ⋯ , ∂ ∂ θ S ] T \nabla_{\theta}=\left[\frac{\partial}{\partial \theta_{1}}, \frac{\partial}{\partial \theta_{2}}, \cdots, \frac{\partial}{\partial \theta_{S}}\right]^{T} ∇θ=[∂θ1∂,∂θ2∂,⋯,∂θS∂]T
若似然函数满足连续可导的条件,则最大似然估计量就是如下方程的解。
∇ θ H ( θ ) = ∇ θ ln l ( θ ) = ∑ i = 1 N ∇ θ ln P ( x i ∣ θ ) = 0 \nabla_{\theta} H(\theta)=\nabla_{\theta} \ln l(\theta)=\sum_{i=1}^{N} \nabla_{\theta} \ln P\left(x_{i} \mid \theta\right)=0 ∇θH(θ)=∇θlnl(θ)=i=1∑N∇θlnP(xi∣θ)=0
方程的解只是一个估计值,只有在样本数趋于无限多的时候,它才会接近于真实值。 - 贝叶斯估计
不同于ML估计,不再把参数 θ θ θ看成一个未知的确定变量,而是看成未知的随机变量,通过对第 i i i类样本 D i D_i Di的观察,使概率密度分布 P ( D i ∣ θ ) P(D_i|θ) P(Di∣θ)转化为后验概率 P ( θ ∣ D i ) P\left(\theta \mid D_{i}\right) P(θ∣Di) ,再求贝叶斯估计。
假设: 将待估计的参数看作符合某种先验概率分布的随机变量。
基本原理:
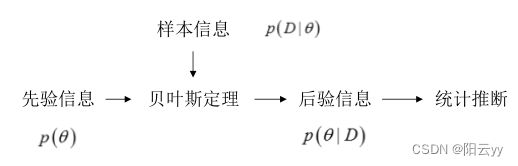
贝叶斯估计的本质: 贝叶斯估计的本质是通过贝叶斯决策得到参数 θ \theta θ 的最优估计,使得总期望风险最小。
P ( θ ) \mathrm{P}(\theta) P(θ) 是待估计参数 θ \theta θ 的先验概率, θ \theta θ 取值与样本集 D = { x 1 , x 2 , ⋯ x N } D=\left\{x_{1}, x_{2}, \cdots x_{N}\right\} D={x1,x2,⋯xN} 有关, λ ( θ ^ , θ ) \lambda(\hat{\theta}, \theta) λ(θ^,θ) 是 θ ^ \hat{\theta} θ^ 作为 θ \theta θ 的估计量时的损失函数。
定义样本下的条件风险为:
R ( θ ^ ∣ x ) = ∫ θ λ ( θ ^ , θ ) P ( θ ∣ x ) d θ R(\hat{\theta} \mid x)=\int_{\theta} \lambda(\hat{\theta}, \theta) P(\theta \mid x) d \theta R(θ^∣x)=∫θλ(θ^,θ)P(θ∣x)dθ
则有:
R = ∫ E d R ( θ ^ ∣ x ) P ( x ) d x R=\int_{E^{d}} R(\hat{\theta} \mid x) P(x) d x R=∫EdR(θ^∣x)P(x)dx
又 R ( θ ^ ∣ x ) R(\hat{\theta} \mid x) R(θ^∣x) 非负, 则由贝叶斯决策知, 求 R \mathrm{R} R 最小即求 R ( θ ^ ∣ x ) R(\hat{\theta} \mid x) R(θ^∣x) 最小。
即:
θ ∗ = arg min R ( θ ^ ∣ x ) \theta^{*}=\arg \min R(\hat{\theta} \mid x) θ∗=argminR(θ^∣x)
可得最优估计: θ ∗ = ∫ Θ θ P ( θ ∣ x ) d θ \theta^{*}=\int_{\Theta} \theta P(\theta \mid x) d \theta θ∗=∫ΘθP(θ∣x)dθ
损失函数: 通常规定函数是一个二次函数,即平方误差损失函数:
λ ( θ ^ , θ ) = ( θ − θ ^ ) 2 \lambda(\hat{\theta}, \theta)=(\theta-\hat{\theta})^{2} λ(θ^,θ)=(θ−θ^)2
可以证明,如果采用平方误差损失函数,则的贝叶斯估计值 θ ^ \hat{\theta} θ^ :是在给定x时 Θ \Theta Θ 的条件期望。
θ ^ = E [ θ ∣ x ] = ∫ Θ θ P ( θ ∣ x ) d θ \hat{\theta}=E[\theta \mid x]=\int_{\Theta} \theta P(\theta \mid x) d \theta θ^=E[θ∣x]=∫ΘθP(θ∣x)dθ
同理可得,在给定样本集D下, θ \theta θ 的贝叶斯估计值是:
θ ^ = E [ θ ∣ D ] = ∫ Θ θ P ( θ ∣ D ) d θ \hat{\theta}=E[\theta \mid D]=\int_{\Theta} \theta P(\theta \mid D) d \theta θ^=E[θ∣D]=∫ΘθP(θ∣D)dθ
贝叶斯估计的基本步骤(基于平方误差损失函数)
1、确定参数 θ \theta θ 的先验分布 P ( θ ) P(\theta) P(θ);
2、由样本集 D = { x 1 , x 2 , ⋯ x N } D=\left\{x_{1}, x_{2}, \cdots x_{N}\right\} D={x1,x2,⋯xN} 求出样本联合分布 P ( D ∣ θ ) P(D \mid \theta) P(D∣θ), 它是 θ \theta θ 的函数:
P ( D ∣ θ ) = ∏ n = 1 N P ( x n ∣ θ ) P(D \mid \theta)=\prod_{n=1}^{N} P\left(x_{n} \mid \theta\right) P(D∣θ)=n=1∏NP(xn∣θ)
3、利用贝叶斯公式, 求 θ \theta θ 的后验分布:
P ( θ ∣ D ) = P ( D ∣ θ ) P ( θ ) ∫ Θ P ( D ∣ θ ) P ( θ ) d θ P(\theta \mid D)=\frac{P(D \mid \theta) P(\theta)}{\int_{\Theta} P(D \mid \theta) P(\theta) d \theta} P(θ∣D)=∫ΘP(D∣θ)P(θ)dθP(D∣θ)P(θ)
4、求出贝叶斯估计值:
θ ^ = ∫ Θ θ P ( θ ∣ D ) d θ \hat{\theta}=\int_{\Theta} \theta P(\theta \mid D) d \theta θ^=∫ΘθP(θ∣D)dθ
五、示例分析
以西瓜书机器学习示例来了解朴素贝叶斯算法过程
数据集:
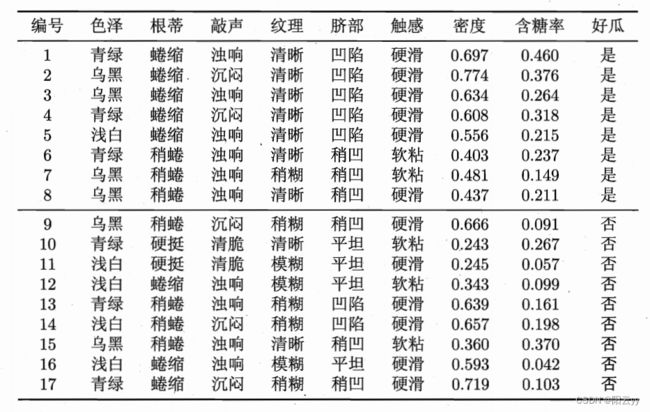
测试数据:

概率分布函数
对连续属性可考虑概率密度函数, 假定 p ( x i ∣ c ) ∼ N ( μ c , i , σ c , i 2 ) p\left(x_{i} \mid c\right) \sim \mathcal{N}\left(\mu_{c, i}, \sigma_{c, i}^{2}\right) p(xi∣c)∼N(μc,i,σc,i2), 其中 μ c , i \mu_{c, i} μc,i 和 σ c , i 2 \sigma_{c, i}^{2} σc,i2 分别是第 c c c 类样本在第 i i i 个属性上取值的均值和方差, 则有
p ( x i ∣ c ) = 1 2 π σ c , i exp ( − ( x i − μ c , i ) 2 2 σ c , i 2 ) p\left(x_{i} \mid c\right)=\frac{1}{\sqrt{2 \pi} \sigma_{c, i}} \exp \left(-\frac{\left(x_{i}-\mu_{c, i}\right)^{2}}{2 \sigma_{c, i}^{2}}\right) p(xi∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)
- 先验概率 P ( c ) P(c) P(c)
P ( P( P( 好瓜 = = = 是 ) = 8 17 ≈ 0.471 )=\frac{8}{17} \approx 0.471 )=178≈0.471
P ( P( P( 好瓜 = = = 否 ) = 9 17 ≈ 0.529 )=\frac{9}{17} \approx 0.529 )=179≈0.529 - 每个属性条件概率 P ( x i ∣ c ) P\left(x_{i} \mid c\right) P(xi∣c) :
P 青绿 ∣ 是 = P ( P_{\text {青绿 } \mid \text { 是 }}=P( P青绿 ∣ 是 =P( 色泽 = = = 青绿 ∣ \mid ∣ 好瓜 = = = 是 ) = 3 8 = 0.375 )=\frac{3}{8}=0.375 )=83=0.375,
P 青绿|否 = P ( P_{\text {青绿|否 }}=P( P青绿|否 =P( 色泽 = = = 青绿 ∣ \mid ∣ 好瓜 = = = 否 ) = 3 9 ≈ 0.333 )=\frac{3}{9} \approx 0.333 )=93≈0.333 ,
P 蜷缩|是 = P ( P_{\text {蜷缩|是 }}=P( P蜷缩|是 =P( 根蒂 = = = 蜷缩 ∣ \mid ∣ 好瓜 = = = 是 ) = 5 8 = 0.375 )=\frac{5}{8}=0.375 )=85=0.375,
P 蜷缩|否 = P ( P_{\text {蜷缩|否 }}=P( P蜷缩|否 =P( 根蒂 = = = 蜷缩 ∣ \mid ∣ 好瓜 = = = 否 ) = 3 9 ≈ 0.333 )=\frac{3}{9} \approx 0.333 )=93≈0.333,
P 浊响|是 = P ( P_{\text {浊响|是 }}=P( P浊响|是 =P( 敲声 = = = 浊响 ∣ \mid ∣ 好瓜 = = = 是 ) = 6 8 = 0.750 )=\frac{6}{8}=0.750 )=86=0.750,
P 浊响|否 = P ( P_{\text {浊响|否 }}=P( P浊响|否 =P( 敲声 = = = 浊响 ∣ \mid ∣ 好瓜 = = = 否 ) = 4 9 ≈ 0.444 )=\frac{4}{9} \approx 0.444 )=94≈0.444,
P 清晰 ∣ 是 = P ( P_{\text {清晰 } \mid \text { 是 }}=P( P清晰 ∣ 是 =P( 纹理 = = = 清晰 ∣ \mid ∣ 好瓜 = = = 是 ) = 7 8 = 0.875 )=\frac{7}{8}=0.875 )=87=0.875,
P 清晰 ∣ 否 = P ( P_{\text {清晰 } \mid \text { 否 }}=P( P清晰 ∣ 否 =P( 纹理 = = = 清晰 ∣ \mid ∣ 好瓜 = = = 否 ) = 2 9 ≈ 0.222 )=\frac{2}{9} \approx 0.222 )=92≈0.222,
P 凹陷|是 = P ( P_{\text {凹陷|是 }}=P( P凹陷|是 =P( 脐部 = = = 凹陷 ∣ \mid ∣ 好瓜 = = = 是 ) = 6 8 = 0.750 )=\frac{6}{8}=0.750 )=86=0.750,
P 凹陷|否 = P ( P_{\text {凹陷|否 }}=P( P凹陷|否 =P( 脐部 = = = 凹陷 ∣ \mid ∣ 好瓜 = = = 否 ) = 2 9 ≈ 0.222 )=\frac{2}{9} \approx 0.222 )=92≈0.222,
P 硬滑|是 = P ( P_{\text {硬滑|是 }}=P( P硬滑|是 =P( 触感 = = = 硬滑 ∣ \mid ∣ 好瓜 = = = 是 ) = 6 8 = 0.750 )=\frac{6}{8}=0.750 )=86=0.750,
P 硬滑|否 = P ( P_{\text {硬滑|否 }}=P( P硬滑|否 =P( 触感 = = = 硬滑 ∣ \mid ∣ 好瓜 = = = 否 ) = 6 9 ≈ 0.667 )=\frac{6}{9} \approx 0.667 )=96≈0.667,
p 密度: 0.697 ∣ 是 = p ( p_{\text {密度: } 0.697 \mid \text { 是 }}=p( p密度: 0.697∣ 是 =p( 密度 = 0.697 ∣ =0.697 \mid =0.697∣ 好瓜 = = = 是 ) ) )
= 1 2 π ⋅ 0.129 exp ( − ( 0.697 − 0.574 ) 2 2 ⋅ 0.12 9 2 ) ≈ 1.959 , =\frac{1}{\sqrt{2 \pi} \cdot 0.129} \exp \left(-\frac{(0.697-0.574)^{2}}{2 \cdot 0.129^{2}}\right) \approx 1.959 \text {, } =2π⋅0.1291exp(−2⋅0.1292(0.697−0.574)2)≈1.959,
p 密度: 0.697 ∣ 否 = p ( p_{\text {密度: } 0.697 \mid \text { 否 }}=p( p密度: 0.697∣ 否 =p( 密度 = 0.697 ∣ =0.697 \mid =0.697∣ 好瓜 = = = 否 ) ) )
= 1 2 π ⋅ 0.195 exp ( − ( 0.697 − 0.496 ) 2 2 ⋅ 0.19 5 2 ) ≈ 1.203 , =\frac{1}{\sqrt{2 \pi} \cdot 0.195} \exp \left(-\frac{(0.697-0.496)^{2}}{2 \cdot 0.195^{2}}\right) \approx 1.203 \text {, } =2π⋅0.1951exp(−2⋅0.1952(0.697−0.496)2)≈1.203,
p 含糖: 0.460 ∣ 是 = p ( p_{\text {含糖: } 0.460 \mid \text { 是 }}=p( p含糖: 0.460∣ 是 =p( 含糖率 = 0.460 ∣ =0.460 \mid =0.460∣ 好瓜 = = = 是 ) ) )
= 1 2 π ⋅ 0.101 exp ( − ( 0.460 − 0.279 ) 2 2 ⋅ 0.10 1 2 ) ≈ 0.788 =\frac{1}{\sqrt{2 \pi} \cdot 0.101} \exp \left(-\frac{(0.460-0.279)^{2}}{2 \cdot 0.101^{2}}\right) \approx 0.788 =2π⋅0.1011exp(−2⋅0.1012(0.460−0.279)2)≈0.788
p 含磧: 0.460 ∣ 否 = p ( p_{\text {含磧: } 0.460 \mid \text { 否 }}=p( p含磧: 0.460∣ 否 =p( 含糖率 = 0.460 ∣ =0.460 \mid =0.460∣ 好瓜 = = = 否 ) ) )
= 1 2 π ⋅ 0.108 exp ( − ( 0.460 − 0.154 ) 2 2 ⋅ 0.10 8 2 ) ≈ 0.066 =\frac{1}{\sqrt{2 \pi} \cdot 0.108} \exp \left(-\frac{(0.460-0.154)^{2}}{2 \cdot 0.108^{2}}\right) \approx 0.066 =2π⋅0.1081exp(−2⋅0.1082(0.460−0.154)2)≈0.066 - 朴素贝叶斯计算
P ( 好瓜 = 是 ) × P 青绿 ∣ 是 × P 蜷缩 ∣ 是 × P 浊响 ∣ 是 × P 清晰 ∣ 是 × P 凹陷 ∣ 是 × P 硬滑 ∣ 是 × p 密度 : 0.697 ∣ 是 × p 含糖 : 0.460 ∣ 是 ≈ 0.038 P(\text{好瓜}=\text{是})\times P_{青绿\mid是}\times P_{蜷缩\mid是}\times P_{浊响\mid是}\times P_{清晰\mid是}\times P_{凹陷\mid是}\times P_{硬滑\mid是}\times p_{密度:0.697\mid是}\times p_{含糖:0.460\mid是}\approx0.038 P(好瓜=是)×P青绿∣是×P蜷缩∣是×P浊响∣是×P清晰∣是×P凹陷∣是×P硬滑∣是×p密度:0.697∣是×p含糖:0.460∣是≈0.038
P ( 好瓜 = 否 ) × P 青绿 ∣ 否 × P 蜷缩 ∣ 否 × P 浊响 ∣ 否 × P 清晰 ∣ 否 × P 凹陷 ∣ 否 × P 硬滑 ∣ 否 × p 密度 : 0.697 ∣ 否 × p 含糖 : 0.460 ∣ 否 ≈ 6.8 × 1 0 − 5 P(\text{好瓜}=\text{否})\times P_{青绿\mid否}\times P_{蜷缩\mid否}\times P_{浊响\mid否}\times P_{清晰\mid否}\times P_{凹陷\mid否}\times P_{硬滑\mid否}\times p_{密度:0.697\mid否}\times p_{含糖:0.460\mid否}\approx6.8\times10^{-5} P(好瓜=否)×P青绿∣否×P蜷缩∣否×P浊响∣否×P清晰∣否×P凹陷∣否×P硬滑∣否×p密度:0.697∣否×p含糖:0.460∣否≈6.8×10−5
由于 0.038 > 6.80 × 1 0 − 5 0.038>6.80 \times 10^{-5} 0.038>6.80×10−5, 因此, 朴素贝叶斯分类器将测试样本 “测 1 ” 判别为 “好瓜”.
六、拉普拉斯平滑修正
对离散属性而言, 令 D c , x i D_{c, x_{i}} Dc,xi 表示 D c D_{c} Dc 中在第 i i i 个属性上取值为 x i x_{i} xi 的样本组成的 集合, 则条件概率 P ( x i ∣ c ) P\left(x_{i} \mid c\right) P(xi∣c) 可估计为
P ( x i ∣ c ) = ∣ D c , x i ∣ ∣ D c ∣ P\left(x_{i} \mid c\right)=\frac{\left|D_{c, x_{i}}\right|}{\left|D_{c}\right|} P(xi∣c)=∣Dc∣∣Dc,xi∣
若某个属性值在训练集中没有与某个类同时出现过, 则直接基于进行概率估计, 再根据朴素贝叶斯进行判别将出现问题. 例如, 在使用西瓜数据集训练朴素贝叶斯分类器时, 对一个 “敲声=清脆” 的测试例, 有
P 清晰|是 = P ( 敲声 = 清脆 ∣ 好瓜 = 是 ) = 0 8 = 0 , P_{\text {清晰|是 }}=P(\text { 敲声 }=\text { 清脆 } \mid \text { 好瓜 }=\text { 是 })=\frac{0}{8}=0, P清晰|是 =P( 敲声 = 清脆 ∣ 好瓜 = 是 )=80=0,
由于朴素贝叶斯的连乘式计算出的概率值为零, 因此, 无论该样本的其他属性是什 么, 哪怕在其他属性上明显像好瓜, 分类的结果都将是 “好瓜=否”, 这显然不太合理.
为了避免其他属性携带的信息被训练集中末出现的属性值“抺去”, 在估计概率值时通常要进行 “平滑”, 常用 “拉普拉斯修正” . 具体来说, 令 N N N 表示训练集 D D D 中可能的类别数, N i N_{i} Ni 表示第 i i i 个属性可能的取值数, 参数估计修正为
P ^ ( c ) = ∣ D c ∣ + 1 ∣ D ∣ + N , P ^ ( x i ∣ c ) = ∣ D c , x i ∣ + 1 ∣ D c ∣ + N i . \begin{aligned} \hat{P}(c) &=\frac{\left|D_{c}\right|+1}{|D|+N}, \\ \hat{P}\left(x_{i} \mid c\right) &=\frac{\left|D_{c, x_{i}}\right|+1}{\left|D_{c}\right|+N_{i}} . \end{aligned} P^(c)P^(xi∣c)=∣D∣+N∣Dc∣+1,=∣Dc∣+Ni∣Dc,xi∣+1.
先验概率可估计为
P ^ ( 好瓜 = 是 ) = 8 + 1 17 + 2 ≈ 0.474 , P ^ ( 好瓜 = 否 ) = 9 + 1 17 + 2 ≈ 0.526 . \hat{P}(\text { 好瓜 }=\text { 是 })=\frac{8+1}{17+2} \approx 0.474, \hat{P}(\text { 好瓜 }=\text { 否 })=\frac{9+1}{17+2} \approx 0.526 \text {. } P^( 好瓜 = 是 )=17+28+1≈0.474,P^( 好瓜 = 否 )=17+29+1≈0.526.
P 青绿 ∣ 是 和 P 青绿 ∣ 否 P_{\text {青绿}\mid \text{是}}和P_{\text {青绿}\mid \text{否}} P青绿∣是和P青绿∣否可估计为
P ^ 青绿 ∣ 是 = P ^ ( 色泽 = 青绿 ∣ 好瓜 = 是 ) = 3 + 1 8 + 3 ≈ 0.364 \hat{P}_{\text {青绿}\mid \text{是}}=\hat{P}(\text { 色泽 }=\text { 青绿 } \mid \text { 好瓜 }=\text { 是 })=\frac{3+1}{8+3} \approx 0.364 P^青绿∣是=P^( 色泽 = 青绿 ∣ 好瓜 = 是 )=8+33+1≈0.364
P ^ 青绿 ∣ 否 = P ^ ( 色泽 = 青绿 ∣ 好瓜 = 否 ) = 3 + 1 9 + 3 ≈ 0.333. \hat{P}_{\text {青绿 }\mid \text { 否 }}=\hat{P}(\text { 色泽 }=\text { 青绿 } \mid \text { 好瓜 }=\text { 否 })=\frac{3+1}{9+3} \approx 0.333 . P^青绿 ∣ 否 =P^( 色泽 = 青绿 ∣ 好瓜 = 否 )=9+33+1≈0.333.
P ^ 清脆|是 = P ^ ( 敲声 = 清脆 ∣ 好瓜 = 是 ) = 0 + 1 8 + 3 ≈ 0.091. \hat{P}_{\text {清脆|是}}=\hat{P}(\text { 敲声 }=\text { 清脆 } \mid \text { 好瓜 }=\text { 是 })=\frac{0+1}{8+3} \approx 0.091 . P^清脆|是=P^( 敲声 = 清脆 ∣ 好瓜 = 是 )=8+30+1≈0.091.
拉普拉斯修正避免了因训练集样本不充分而导致概率估值为零的问题, 并且在训练集变大时, 修正过程所引入的先验(prior)的影响也会逐渐变得可忽略, 使得估值渐趋向于实际概率值.
七、算法优缺点
优点
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
缺点
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别 的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效 果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致 预测效果不佳。
- 由于是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
- 对输入数据的表达形式很敏感。
八、python实现
8.1 sklearn贝叶斯
常用的有3个朴素贝叶斯的分类算法:
| 算法名称 | 适用条件 |
|---|---|
| 高斯分布的朴素贝叶斯(GaussianNB) | 样本特征的分布大部分是连续值,适合正态分布 |
| 多项式分布的朴素贝叶斯(MultinomialNB) | 样本特征的分大部分是多元离散值,适合二项式分布 |
| 伯努利分布的朴素贝叶斯(BernoulliNB) | 样本特征是二元离散值或者很稀疏的多元离散值,适合二项分布 |
naive_bayes.GaussianNB
参数:
先验概率priors,对应 Y Y Y的各个类别的先验概率 P ( Y = c k ) P(Y=c_k) P(Y=ck) 。这个值默认不给出,如果不给出此时 P ( Y = c k ) = m k / m P(Y=c_k)=m k / m P(Y=ck)=mk/m 。
其中 m m m 为训练集样本总数量, m k m k mk 为输出为第 k k k 类别的训练集样本数。
预测方法:
- predict: 方法就是我们最常用的预测方法,直接给出测试集的预测类别输出。
- predict_proba:则不同,它会给出测试集样本在各个类别上预测的概率。容易理解,predict_proba预测出的各个类别概率里的最大 值对应的类别,也就是predict方法得到类别。
- predict_log_proba: 和predict_proba类似它会给出测试集样本在各个类别上预测的概率的一个对数转化。转化后predict_log_proba 预测出的各个类别对数概率里的最大值对应的类别,也就是predict方法得到类别。
重要方法:
partial_fit:如果训练集数据量非常大,一次不能全部载入内存的时候。可以把训练集分成若干等分,重复调用partial_fit来一步步的学习训练集。
naive_bayes.MultinomialNB
参数:
alpha浮点型可选参数,默认为1.0,其实就是添加拉普拉斯平滑,如果这个参数设置为0,就是不添加平滑;布尔参数fit_prior表示是否要考虑先验概率,如果是false, 则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数 class_priori让MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为 P ( Y = c k ) = m k / m \mathrm{P}(\mathrm{Y}=\mathrm{c_k})=\mathrm{mk} / \mathrm{m} P(Y=ck)=mk/m 。其中 m \mathrm{m} m 为训练集样本总数量, m k \mathrm{mk} mk 为输出为第k类别的训练集样本数。
| fit_prior | class_prior | 最终先验概率 |
|---|---|---|
| False | 填或不填没有意义 | P ( Y = c k ) = 1 / k P ( Y = c k ) = 1 / k P(Y=c_k)=1 / k P(Y=c_k)=1 / k P(Y=ck)=1/kP(Y=ck)=1/k |
| True | 不填 | P ( Y = c k ) = m k / m P ( Y = c k ) = m k / m P(Y=c_k)=mk / m P(Y=c_k)=mk / m P(Y=ck)=mk/mP(Y=ck)=mk/m |
| True | 填 | P ( Y = c k ) = p ( Y = c k ) = c l a s s _ p r i o r P(Y=c_k)=p(Y=c_k)=class\_prior P(Y=ck)=p(Y=ck)=class_prior |
naive_bayes.BernoulliNB
BernoulliNB一共有4个参数,其中3个参数的名字和意义和MultinomialNB完全相同。唯一增加的一个参数是binarize。这个参数主要是用来帮BernoulliNB处理二项分布的,可以是数值或者不输入。如果不输入,则BernoulliNB认为每个数据特征都已经是二元的。否则的话,小于binarize的会归为一类,大于binarize的会归为另外一类。
在使用BernoulliNB的fit或者partial_fit方法拟合数据后,我们可以进行预测。此时预测有三种方法,包括predict,predict_log_proba和predict_proba。方法和GaussianNB完全一样。
8.2 文本情感分析示例
数据来源情感分析-朴素贝叶斯
- 导入数据
数据包括评论内容以及分类标签
import pandas as pd
data = pd.read_excel('data_test_train.xlsx')
data.head()
comment sentiment
0 口味:不知道是我口高了,还是这家真不怎么样。??我感觉口味确实很一般很一般。上菜相当快,我敢... 0
1 菜品丰富质量好,服务也不错!很喜欢! 1
2 说真的,不晓得有人排队的理由,香精香精香精香精,拜拜! 0
3 菜量实惠,上菜还算比较快,疙瘩汤喝出了秋日的暖意,烧茄子吃出了大阪烧的味道,想吃土豆片也是口... 1
4 先说我算是娜娜家风荷园开业就一直在这里吃??每次出去回来总想吃一回??有时觉得外面的西式简餐... 1
- 数据预处理
对中文数据进行切分成词,导入jieba库
jieba.cut(s) 精确模式:把文本精确的切分开,不存在冗余单词;
jieba.lcut(s,cut_all=True) 全模式:把文本中所有可能的词语都扫描出来,有冗余;
jieba.lcut_for_search(s) 搜索引擎模式:在精确模式基础上,对长词再次切分
#根据需要做处理,去重、去除停用词
# jieba分词
import jieba
def chinese_word_cut(mytext):
return " ".join(jieba.cut(mytext))
data['cut_comment'] = data.comment.apply(chinese_word_cut)
data.head()
comment ... cut_comment
0 口味:不知道是我口高了,还是这家真不怎么样。??我感觉口味确实很一般很一般。上菜相当快,我敢... ... 口味 : 不 知道 是 我口 高 了 , 还是 这家 真 不怎么样 。 ? ? 我 感觉 口...
1 菜品丰富质量好,服务也不错!很喜欢! ... 菜品 丰富 质量 好 , 服务 也 不错 ! 很 喜欢 !
2 说真的,不晓得有人排队的理由,香精香精香精香精,拜拜! ... 说真的 , 不 晓得 有人 排队 的 理由 , 香精 香精 香精 香精 , 拜拜 !
3 菜量实惠,上菜还算比较快,疙瘩汤喝出了秋日的暖意,烧茄子吃出了大阪烧的味道,想吃土豆片也是口... ... 菜量 实惠 , 上菜 还 算 比较 快 , 疙瘩汤 喝出 了 秋日 的 暖意 , 烧茄子 吃...
4 先说我算是娜娜家风荷园开业就一直在这里吃??每次出去回来总想吃一回??有时觉得外面的西式简餐... ... 先说 我 算是 娜娜 家风 荷园 开业 就 一直 在 这里 吃 ? ? 每次 出去 回来 总...
- 提取特征
CountVectorizer是属于常见的特征数值计算类,是一个文本特征提取方法。对于每一个训练文本,它只考虑每种词汇在该训练文本中出现的频率。
CountVectorizer会将文本中的词语转换为词频矩阵,它通过fit_transform函数计算各个词语出现的次数。
CountVectorizer是通过fit_transform函数将文本中的词语转换为词频矩阵,矩阵元素a[i][j] 表示j词在第i个文本下的词频。即各个词语出现的次数,通过get_feature_names()可看到所有文本的关键字,通过toarray()可看到词频矩阵的结果。
CountVectorizer参数:
CountVectorizer(input='content', encoding='utf-8', decode_error='strict', strip_accents=None, lowercase=True, preprocessor=None, tokenizer=None, stop_words=None,
token_pattern='(?u)\b\w\w+\b', ngram_range=(1, 1), analyzer='word', max_df=1.0, min_df=1, max_features=None, vocabulary=None, binary=False, dtype=<class 'numpy.int64'>)
| 参数 | 作用 |
|---|---|
| analyzer | 一般使用默认,可设置为string类型,如’word’, ‘char’, ‘char_wb’,还可设置为callable类型,比如函数是一个callable类型 |
| preprocessor | 设为None或callable类型 |
| tokenizer | 设为None或callable类型 |
| ngram_range | 词组切分的长度范围,待详解 |
| stop_words | 设置停用词,设为english将使用内置的英语停用词,设为一个list可自定义停用词,设为None不使用停用词,设为None且max_df∈[0.7, 1.0)将自动根据当前的语料库建立停用词表 |
| lowercase | 将所有字符变成小写 |
| token_pattern | 过滤规则,表示token的正则表达式,需要设置analyzer == ‘word’,默认的正则表达式选择2个及以上的字母或数字作为token,标点符号默认当作token分隔符,而不会被当作token |
| max_df | 可以设置为范围在[0.0 1.0]的float,也可以设置为没有范围限制的int,默认为1.0。这个参数的作用是作为一个阈值,当构造语料库的关键词集的时候,如果某个词的document frequence大于max_df,这个词不会被当作关键词。如果这个参数是float,则表示词出现的次数与语料库文档数的百分比,如果是int,则表示词出现的次数。如果参数中已经给定了vocabulary,则这个参数无效 |
| min_df | 类似于max_df,不同之处在于如果某个词的document frequence小于min_df,则这个词不会被当作关键词 |
| max_features | 默认为None,可设为int,对所有关键词的term frequency进行降序排序,只取前max_features个作为关键词集 |
| vocabulary | 默认为None,自动从输入文档中构建关键词集,也可以是一个字典或可迭代对象? |
| binary | 默认为False,一个关键词在一篇文档中可能出现n次,如果binary=True,非零的n将全部置为1,这对需要布尔值输入的离散概率模型的有用的 |
| dtype | 使用CountVectorizer类的fit_transform()或transform()将得到一个文档词频矩阵,dtype可以设置这个矩阵的数值类型 |
| 属性表 | 作用 |
|---|---|
| vocabulary_ | 词汇表;字典型 |
| get_feature_names() | 所有文本的词汇;列表型 |
| stop_words_ | 返回停用词表 |
| 方法表 | 作用 |
|---|---|
| fit_transform(X) | 拟合模型,并返回文本矩阵 |
| fit(raw_documents[, y]) | Learn a vocabulary dictionary of all tokens in the raw documents. |
| fit_transform(raw_documents[, y]) | Learn the vocabulary dictionary and return term-document matrix. |
from sklearn.feature_extraction.text import CountVectorizer
def get_custom_stopwords(stop_words_file):
with open(stop_words_file) as f:
stopwords = f.read()
stopwords_list = stopwords.split('\n')
custom_stopwords_list = [i for i in stopwords_list]
return custom_stopwords_list
stop_words_file = '哈工大停用词表.txt'
stopwords = get_custom_stopwords(stop_words_file)
vect = CountVectorizer(max_df = 0.8,
min_df = 3,
token_pattern=u'(?u)\\b[^\\d\\W]\\w+\\b',
stop_words=frozenset(stopwords))
- 划分数据集
X = data['cut_comment']
y = data.sentiment
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=22)
- 特征展示
test = pd.DataFrame(vect.fit_transform(X_train).toarray(), columns=vect.get_feature_names())
test.head()
ipad ok ps wifi 一下 一个个 一个半 一个多 ... 麻酱 麻麻 黄瓜 黄盖 黄色 黏糊糊 黑椒 默默
0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0
3 0 1 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0
- 训练模型
from sklearn.naive_bayes import MultinomialNB
nb = MultinomialNB()
X_train_vect = vect.fit_transform(X_train)
nb.fit(X_train_vect, y_train)
train_score = nb.score(X_train_vect, y_train)
train_score
训练得分
0.899375
- 测试模型
X_test_vect = vect.transform(X_test)
nb.score(X_test_vect, y_test)
0.8275
- 分析数据
data = pd.read_excel("data.xlsx")
data['cut_comment'] = data.comment.apply(chinese_word_cut)
X=data['cut_comment']
X_vec = vect.transform(X)
nb_result = nb.predict(X_vec)
data['nb_result'] = nb_result
test = pd.DataFrame(vect.fit_transform(X).toarray(), columns=vect.get_feature_names())
test.head()
# 结果写入excel
data.to_excel("data_result.xlsx",index=False)
8.3 CountVectorizer()函数
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
texts=["orange banana apple grape","banana apple apple","grape", 'orange apple']
cv = CountVectorizer()
cv_fit=cv.fit_transform(texts)
print(cv.vocabulary_)
print(cv_fit)
print(cv_fit.toarray())
输出如下:
{'orange': 3, 'banana': 1, 'apple': 0, 'grape': 2} #这里是根据首字母顺序,将texts变量中所有单词进行排序,apple首字母为a所以 # 排第一,banana首字母为b所以排第二
(0, 2) 1 # (0, 2) 1 中0表示第一个字符串"orange banana apple grape";2对应上面的'grape': 2;1表示出现次数1。整体理 # 解为第一字符串的顺序为二的词语在出现次数为1
(0, 0) 1
(0, 1) 1
(0, 3) 1
(1, 0) 2
(1, 1) 1
(2, 2) 1
(3, 0) 1
(3, 3) 1
[[1 1 1 1] # 第一个字符串,排名0,1,2,3词汇(apple,banana,grape,orange)出现的频率都为1
[2 1 0 0] #第二个字符串,排名0,1,2,3词汇(apple,banana,grape,orange)出现的频率为2,1,00
[0 0 1 0]
[1 0 0 1]]