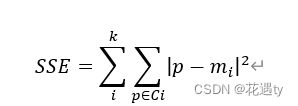kmeans算法详解和python代码实现
kmeans算法详解和python代码实现
kmeans算法
无监督学习和监督学习
监督学习:
是通过已知类别的样本分类器的参数,来达到所要求性能的过程
简单来说,就是让计算机去学习我们已经创建好了的分类模型
像作者之前提到过朴素贝叶斯算法 ,就是一种监督学习。
无监督学习:
指根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题的过程
简单来说就是不知道分类的前提下,让计算机进行学习做事情
其中有个重要的分类就是基于样本相似度的简单聚类方法,而kmeans算法就是其中的代表之一
kmeans算法的理解
有个著名的牧师,村民模型可以用来很好的理解kmeans:
有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有的村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。
牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
kmeans 算法的流程
样本点x[n] #可以理解成村民居住的位置
随机选取k个点means[k] #可以理解成牧师随机选取的点
while(t) :#终止条件
for i in n :
for j in k :
计算每一个样本点和每一个聚类点的代价 #就是牧师和村民的距离
for j in k :
计算每一个样本代价最低的聚类点,并进行归类 #有哪些村民是属于我的
修改聚类点的位置为所在簇中心点的位置 #重新规划聚类点
end
python代码实现
在实现之前 有一个问题,我们会发现聚类的结果和k息息相关,但是我们没办法事先知道k的取值,k太小显然分类结果不够友好,k太大又会导致过度分类,和过拟合一样,也不是一件好事,那么如何选取一个合适的k就是重中之重。
鉴于初学者本文采用最简单的手肘法,方法如下:
SSE(sum of the square errors,误差平方和)
其中Ci为dii个簇,mi为第i个质心,p为属于Ci的数据点。
SSE代表了聚类效果。
def findk(data):
# 确定k值
k = np.arange(1, 11)
ja = []
for i in k:
model = KMeans(n_clusters=i)
model.fit(data)
ja.append(model.inertia_)
# 给这几个点施加标记
plt.annotate(str(i), (i, model.inertia_))
plt.plot(k, ja)
plt.show()
# 经确定,k=4
k = 4
结果如上,所以k取4
函数体属下所示
if __name__ == '__main__':
file = open("testSet.txt", 'r')
data = []
while (True):
dataline = file.readline()
if not dataline:
break
dataline = dataline.split()
data.append([float(dataline[0]), float(dataline[1])]) # 这里是二维数组,可以根据需要自行修改
data = np.array(data)
findk(data)
means, label = kmean(data, 4) #训练
plt.figure()
for j in range(4):
x, y = getallmenas(j, data, label) #按照不同类别进行画图
plt.scatter(x=x, y=y, marker='o', cmap=plt.cm.Paired)
plt.scatter(means[:,0],means[:,1],marker='*',s=80) #画出各个聚点中心的位置
plt.show()
结果如上图所示:
其余代码如下:
# kmeans.py
import random
import numpy as np
import matplotlib.pylab as plt
from sklearn.cluster import KMeans
# 计算两点距离
def distance(a, b):
return np.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)
def kmean(data, k):
n, m = np.shape(data)
means = np.zeros((k, m))
temp = random.sample(range(n), k) # 随机选取k个点作为初始点
for i in range(k):
mean = data[temp[i]]
means[i] = mean
label = np.zeros(n) # 分类结果
con = True
for x in range(10): #此处可以换成所需要的终止条件
oldmeans = np.copy(means)
for i in range(n):
disline = np.zeros(k)
for j in range(k):
dis = distance(data[i], means[j])
disline[j] = dis
label[i] = np.argmin(disline)
for j in range(k):
means[j] = np.mean(data[label == j], axis=0)
return means, label
#获取同类型的点的x,y坐标
def getallmenas(k, data, label):
thedata = data[label == k]
xlist = np.zeros(len(thedata))
ylist = np.zeros(len(thedata))
for i in range(len(thedata)):
xlist[i] = thedata[i][0]
ylist[i] = thedata[i][1]
return xlist, ylist
以上为全部内容。