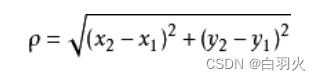机器学习：K近邻算法（K-NN）

 

 K近邻（K-Nearest Neighbor, KNN）是一种最经典和最简单的有监督学习方法之一，它非常有效而且易于掌握。

1 K近邻算法概述

一个样本与数据集中的k个样本最相似， 如果这k个样本中的大多数属于某一个类别， 则该样本也属于这个类别。也就是说，该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时，只与极少量的相邻样本有关。第一个字母k可以小写，表示外部定义的近邻数量。

2 K近邻算法的重点

2.1 距离度量

K近邻算法中一个重要的问题是计算样本之间的距离，以确定训练样本中哪些样本与测试样本更加接近。
​ 在实际应用中，我们往往需要根据应用的场景和数据本身的特点来选择距离计算方法。当已有的距离方法不能满足实际应用需求时，还需要针对性地提出适合具体问题的距离度量方法。k近邻算法对距离的计算方式有多种，其中以Manhattan 距离与Euclidean 距离为主。

​

Manhattan 距离

 ​

                                                                   Euclidean 距离

当已有距离度量方法不能满足需求时，应该探索符合需求的距离度量方法。

2.2 K值的选择

k近邻算法对样本的分类及其依赖于k的取值。k值不可取过大或过小。

一般而言，从k = 1 k = 1k=1开始，随着的逐渐增大，K近邻算法的分类效果会逐渐提升；在增大到某个值后，随着的进一步增大，K近邻算法的分类效果会逐渐下降。

k值越大，模型的偏差越大，对噪声数据越不敏感，当k值很大时，可能造成欠拟合；

k值越小，模型的方差就会越大，当k值太小，就会造成过拟合。

3 K近邻算法的优缺点

优点：精度高，对异常值不敏感，无输入数据假定

缺点：计算复杂度高，空间复杂度高

4 实现K近邻算法

本次实验调用鸢尾花Iris数据集，利用k近邻算法训练该数据集并评估模型准确率。

4.1 介绍鸢尾花Iris数据集

Iris flower数据集是1936年由Sir Ronald Fisher引入的经典多维数据集，可以作为判别分析（discriminant analysis）的样本。该数据集包含Iris花的三个品种(Iris setosa, Iris virginica and Iris versicolor)各50个样本，每个样本还有4个特征参数（分别是萼片的长宽和花瓣的长宽，以厘米为单位）sepal length (cm), sepal width (cm), petal length (cm), petal width (cm)该数据集成为了机器学习中各种分类技术的典型实验案例。

数据集中的数据与结构如下

​

4.2 实现对iris数据集的k近邻算法分类及预测

 一.导入库

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

二.处理数据集

iris = load_iris()
#date为特征数据集
data = iris.get("data")
#target为标记数据集
target = iris.get("target")
#划分测试集占20%
x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=0)

三.定义k值 

KNN = KNeighborsClassifier(n_neighbors=5)

四.评估模型准确率

    KNN.fit(x_train, y_train)
    train_score = KNN.score(x_train, y_train)
    test_score = KNN.score(x_test, y_test)
    print("模型的准确率：", test_score)

五.预测未知种类的样本

prediction = KNN.predict(X1)

完整代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
if __name__ == '__main__':
    iris = load_iris()
    #date为特征数据集
    data = iris.get("data")
    #target为标记数据集
    target = iris.get("target")
    #划分测试集占20%
    x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=0)
    #定义k值
    KNN = KNeighborsClassifier(n_neighbors=5)
    KNN.fit(x_train, y_train)
    train_score = KNN.score(x_train, y_train)
    test_score = KNN.score(x_test, y_test)
    print("模型的准确率：", test_score)
    #定义三个测试数据
    X1 = np.array([[1.9, 2.8, 4.7, 1.1], [5.8, 2.7, 4.1, 1.5], [3.6, 2.5, 3.1, 2.1]])
    prediction = KNN.predict(X1)
    #根据预测值找出对应花名
    a = iris.get("target_names")[prediction]
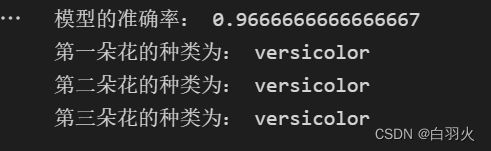
    print("第一朵花的种类为：", a[0])
    print("第二朵花的种类为：", a[1])
    print("第三朵花的种类为：", a[2])

运行结果

 5 实际情况产生的问题

 通过何种方法寻找测试样本的“近邻”，即如何计算样本之间的距离或相似度？

 如何选择K值的大小才能达到最好的预测效果？

 当训练样本或者变量维度很大时，如何更快地进行预测？