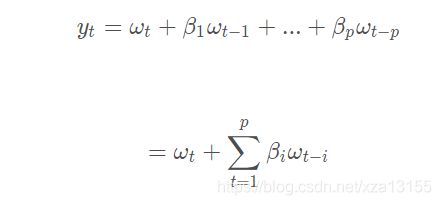时间序列模型——AR、MA、ARMA、ARIMA
这里写目录标题
- 时间序列模型
- 自回归模型
-
- 差分与非平稳序列
-
- 差分
- 检验不平稳
- 移动平均模型
-
- 移动平均法
- MA模型
- ARMA模型
- ARIMA
-
- 建模方法
时间序列模型
常用的时间序列模型有四种:自回归模型 AR( p )、移动平均模型 MA(q)、自回归移动平均模型 ARMA(p,q)、自回归差分移动平均模型 ARIMA(p,d,q), 前三种都是 ARIMA模型的特例。下面介绍这四种模型的原理。
自回归模型
自回归模型(英语:Autoregressive model,简称AR模型),是统计上一种处理时间序列的方法,用同一变数例如x的之前各期,亦即x1至xt-1来预测本期xt的表现,并假设它们为线性关系。因为这是从回归分析中的线性回归发展而来,只是不用x预测y,而是用x预测 x(自己);所以叫做自回归。

X的期望值等于一个或数个滞后变量的线性组合,加常数项,加随机误差。

但是这种方法受到一定的限制:
1,必须具有自相关,如果自相关系数®小于0.5,则不宜采用,否则预测结果极不准确。
2,只适用于预测与自身前期相关的现象,即受自身历史因素影响较大的现象,如矿的开采量,各种自然资源产量等;对于受外因影响较大的现象,不宜采用自回归,而应改采可纳入其他变数的向量自回归模型。
3,适用于宽平稳数据,其特性是序列的统计特性不随时间的平移而变化,即均值和协方差不随时间的平移而变化。
差分与非平稳序列
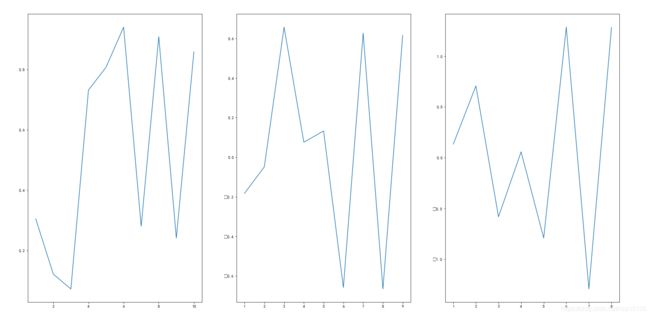
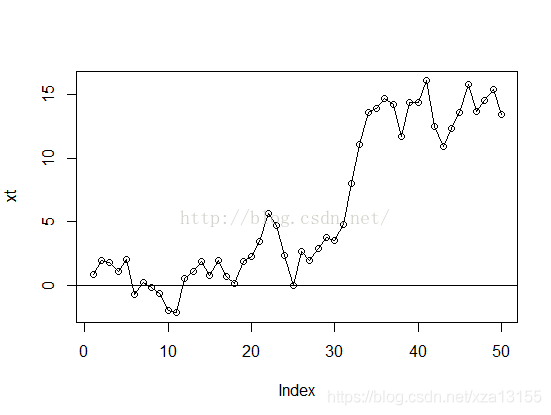
在AR模型中,无法有效预测不平稳的序列。下面的序列通过目视,基本能认为是不平稳的。我们可以使用差分来平稳序列。
差分
**非平稳序列往往一次到两次差分之后,就会变成平稳序列。**什么是差分呢?差分,一般应用与时序分析中,其实就是下一个数值 ,减去上一个数值 。
一阶差分:连续间隔相同两项之差,用下一个数值,减去上一个数值 ,就叫“一阶差分”。
二阶差分:一阶差分的基础上再进行一次差分。
值得注意的一点是,每一次差分之后,都会少一个序列值
from numpy import diff
import matplotlib.pyplot as plt
import random
x=[]
y=[]
for i in range(10):
x.append(i+1)
y.append(random.random())
y1=diff(y,1)
y2=diff(y,2)
plt.subplot(131)
plt.plot(x,y)
plt.subplot(132)
plt.plot(x[0:9],y1)
plt.subplot(133)
plt.plot(x[0:8],y2)
plt.show()
检验不平稳
除了目视这个主观检验的方法外,我们如何通过数学方法来判定一个序列的平稳性呢?可以通过ADF检验平稳性。使用Python的tseries库引入adf函数。
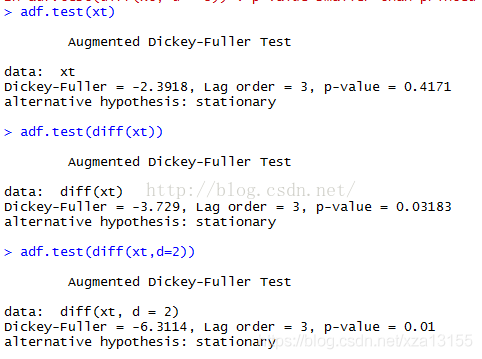
当没有做差分的时候,p-value是0.47,原假设是非平稳时间序列。p-value>0.05的时候,在95%的置信度下,我们不能拒绝原假设的,所以我们不能说xt原序列是时序平稳的,但是在一阶差分和二阶差分后,p值小于0.05,则可以拒绝原假设,认为序列平稳。
移动平均模型
移动平均法
移动平均法是根据时间序列数据逐次运行,每次都计算一定数目的时序平均数, 以一组平均值反映长期趋势。如下面的股票行情曲线的趋势线:

当时间序列的数值由于受周期变动和不规则变动的影响,起伏较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。移动平均法有简单移动平均法,加权移动平均法,趋势移动平均法等。
MA模型
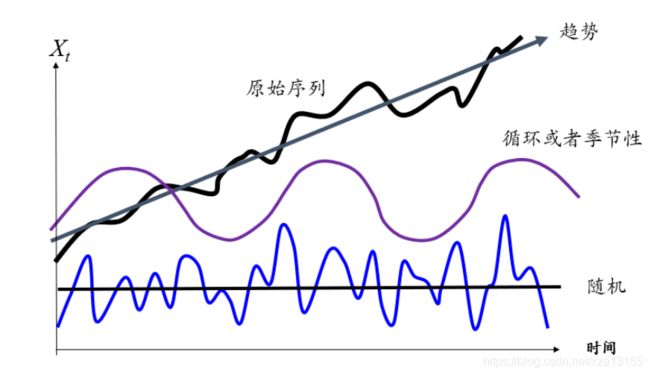
与自回归模型不同,移动平均是以过去的残差项(也就是白噪声)来做线性组合,而AR模型是以过去的观察值来做线性组合。
MA模型的出发点是通过组合残差项来观察残差的振动。
ps:为什么,残差要是白噪声
白噪声就是一系列独立分布的正态序列:序列无相关性,无趋势性,有随机性,它服从均值为0,方差为σ2的正态分布,白噪声的每一个时序点都是服从正态分布的。
拿到数据后一般先进行平稳性检验,然后白噪声检验,如果一个序列是平稳的,那么下面我们就要判断数据是否是白噪声,白噪声没有研究的意义。
得到白噪声序列,就说明时间序列中有用的信息已经被提取完毕了,剩下的全是随机扰动,是无法预测和使用的,残差序列如果通过了白噪声检验,则建模就可以终止了,因为没有信息可以继续提取。如果残差不是白噪声,就说明残差中还有有用的信息,需要修改模型或者进一步提取。
ARMA模型
ARIMA
ARIMA(p,d,q)中,AR是“自回归”,MA为“滑动平均”;即为差分整合移动平均自回归模型。

三个参数:p为自回归阶数;d为使之成为平稳序列所做的差分次数(阶数);q为滑动平均阶数。
建模方法
1,获取时间序列数据,处理为1维向量。
2,数据预处理
平稳性检验和白噪声检验。能够适用ARMA模型进行分析预测的时间序列必须满足的条件是平稳非白噪声序列。
平稳性检验一般通过时序图和相关图来检验时间序列的平稳性。对于非平稳时间序列中若存在增长或下降趋势,则需要进行差分处理然后进行平稳性检验直至平稳为止。其中,差分的次数就是模型ARIMA(p,d,q)的阶数,理论上说,差分的次数越多,对时序信息的非平稳确定性信息的提取越充分,但是从理论上说,差分的次数并非越多越好,每一次差分运算,都会造成信息的损失,所以应当避免过分的差分,一般在应用中,差分的阶数不超过2。
2,模型定阶,在确定了模型的类型之后,还需要知道模型的阶数p和q,采用 自相关系数ACF 图、偏自相关系数PAC 图,AIC 准则(赤道信息量准则)和 BIC 准则(贝叶斯准则)相结合的方式确定。
ACF 指任意时间 t(t=1,2,3…n)的 序列值Xt 与其自身的滞后值(这里取滞后一阶)Xt-1之间的线性关系。ACF图就是指以滞后值(xt-1)为x轴,自相关系数(Xt与Xt-1的相关系数值)为y轴画出的图.
①在尝试不同模型后,选择找出最佳的模型(AIC,BIC最小)
②通过查看图来确定p和q。链接: link.
3,参数估计对模型的参数进行估计的方法通常有相关矩估计法、最小二乘估计以及极大似然估计等。
4,模型的验证模型的验证主要是验证模型的拟合效果
新开通了本人的公众号,欢迎关注:燕南路GISer ,专注GIS干货分享,不定期更新。
主要兴趣:GIS、时空数据挖掘、python、机器学习深度学习
CSDN的部分内容会重写再搬迁到公众号,欢迎关注!
![]()