论文阅读:GraphSNN
2022年ICLR高分论文 GraphSNN
GNN的缺陷
GNN的一个核心思想就是,从邻域结点聚合信息,再和自己的信息combine形成下一层的信息

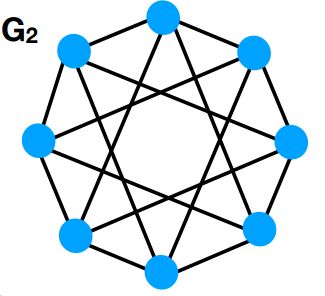
每一个结点的计算图如上图所示。但是这有个前提,就是置换不变性。也就是说B C D的排列顺序对A的结果不影响。这就有个缺点,置换不变性的要求会让GNN损失一部分的邻域结构信息。有时候GNN都不能分辨两张非常简单的图。

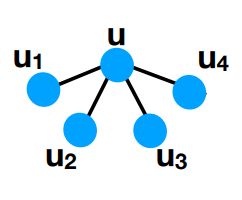
这里是非常简单的两张图,假设我们使用GNN来分类这两张图,每个结点的feature一样,根据传统GNN的计算图来看,这两张图每一个结点的计算图都是这样子的:
由GNN来分辨,这两张图是一模一样的,但是我们可以很简单就知道这两张图并不是一个东西,所以GNN无法分辨这么一个简单图。但是GraphSNN可以解决这个问题。在讲GraphSNN之前,还有一些预备知识要了解
GNN性能的上界:WL-test
WL-test,又叫图同构测试。
那么什么是图同构呢,直观来说就是两张图存在一种一一映射关系,使得G1中所有的边和点在G2中都有对应。举一个简单的例子。判断下面这两张图是否同构:
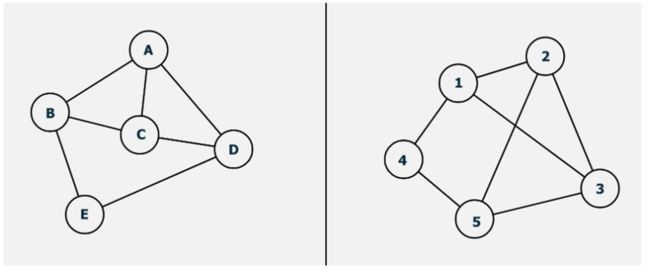
简单的图我们一眼就可以看出来,A->3,B->1;C->2;D->5;E->4 边也一一对应。这两张图同构。
但是复杂一点的图就很难确定了,检测图的同构被认为是一个NP问题,目前最有效的办法是 Weisfeiler-Lehman算法,可以在多项式时间内进行求解。
WL算法可以是K维的,K-维 WL 算法在计算图同构问题时会考虑顶点的 k 元组,如果只考虑顶点的自身特征(如标签、颜色等),那么就是 1-维 WL 算法。有学者已经证明WL-test最多是3维的。
我们在这里介绍一维的算法,因为GraphSNN是和一维的进行比较的。
多重集:一组可能重复的元素的组合,例如{1,1,2, 3,2 }就是一个多重集
WL算法有一个很形象的例子:

a:给出两个标签的label的图G,G’
b:考虑结点邻域的标签,并对此进行排序。(1,1135表示当前结点标签为4,其邻域结点标签排序后为1135)
c:岁标签进行压缩映射
d:得到新的标签
e:迭代一轮之后,利用计数函数得到两张图的计数特征,得到图特征向量就可以计算图之间的相似性了。
对于这个例子来说,G的计数特征向量为(2,1,1,1,1,2,0,1,0,1,1,0,1)前五个数是没被映射之前的标签,label为1的结点有2个,label为2的有1个,label为3的有1个,label为4的有1个,label为5的有1个。后八个数是映射之后的空间,一共被映射到了8个点。映射之后label为6的有两个,label为7的有一个。。。。。。这样以此类推。G’也是同样的操作。然后使用函数计算相似性,判断两张图是否同构。
直观上来看,WL-test 第 k 次迭代时节点的标号表示的是结点高度为 k 的子树结构: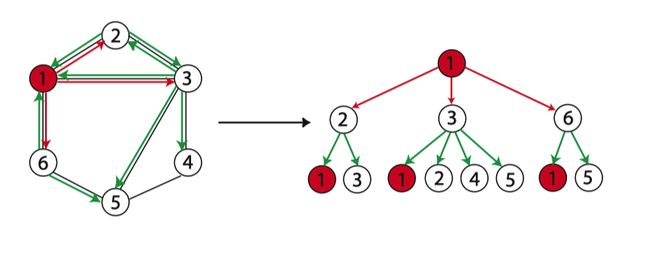
这里的结构和GNN的计算图是不是很相似。
然后有学者证明了,GNN的性能上界是WL-test。具体证明我不在这里写了,感兴趣的读者可以自己搜一下,资料还是比较多的。
但是有了WL-test,依然不能解决之前两张图的分类问题,因为计算图还是一样的。这时候作者提出了GraphSNN,性能超过WL-test
GraphSNN
一些符号表示
简单无向图:G=(V,E)V,E分别是顶点集和边集
顶点v邻居顶点的集合:N(v) ={ u ∈ V ∣ ( u , v ) ∈ E u\in V\vert(u,v)\in E u∈V∣(u,v)∈E} N ~ ( v ) = N ( v ) ⋃ v \widetilde N(v)=N(v)\bigcup v N (v)=N(v)⋃v
顶点v邻居集的子图表示 S v S_v Sv由 N ~ ( v ) \widetilde N(v) N (v)归纳出的G的子图,包含E中的两个端点均属于 N ~ \widetilde N N 的边
顶点u和v的重叠子图表示为 S u v = S u ⋂ S v S_{uv} =S_u\bigcap S_v Suv=Su⋂Sv
顶点v的特征: h v h_v hv
注意:如果 S i S_i Si和 S j S_j Sj是相邻的子图,i 和j不一定是相邻的顶点
三种子图的定义
subgraph-isomorphic(子图同构):如果存在一个双射 g : N ~ ( i ) → N ~ ( i ) g:\widetilde N(i)\rightarrow \widetilde N(i) g:N (i)→N (i)如果g(i)=j使得任意两个顶点 v 1 , v 2 ∈ N ~ ( v ) v_1,v_2\in \widetilde N(v) v1,v2∈N (v) v 1 v_1 v1和 v 2 v_2 v2在 S i S_i Si中相邻当且仅当 g ( v 1 ) , g ( v 2 ) g(v_1),g(v_2) g(v1),g(v2)在 S j S_j Sj中也是相邻的,且 h v 1 = h g ( v 1 ) h_{v_1}=h_{g(v_1)} hv1=hg(v1), h v 2 = h g ( v 2 ) h_{v_2}=h_{g(v_2)} hv2=hg(v2).称 S i S_i Si和 S j S_j Sj子图同构,记为: S i ≅ s u b g r a p h S j S_i\cong{}_{subgraph}S_j Si≅subgraphSj
overlap-isomorphic(重叠同构):如果存在一个双射 g : N ~ ( i ) → N ~ ( i ) g:\widetilde N(i)\rightarrow \widetilde N(i) g:N (i)→N (i),如果g(i)=j使得任意一个顶点 v ′ ∈ N ( i ) v'\in N(i) v′∈N(i)和 g ( v ′ ) = u ′ g(v')=u' g(v′)=u′满足 S i v ′ ≅ s u b g r a p h S j u ′ S_{iv'}\cong{}_{subgraph}S_{ju'} Siv′≅subgraphSju′则称 S i S_i Si和 S j S_j Sj重叠同构,记为: S i ≅ o v e r l a p S j S_i\cong{}_{overlap}S_j Si≅overlapSj
S i v ′ = S i ⋂ S v ′ S_{iv'} =S_i\bigcap S_{v'} Siv′=Si⋂Sv′ S j u ′ = S j ⋂ S u ′ S_{ju'} =S_j\bigcap S_{u'} Sju′=Sj⋂Su′
subtree-isomorphic(子树同构):如果存在一个双射 g : N ~ ( i ) → N ~ ( i ) g:\widetilde N(i)\rightarrow \widetilde N(i) g:N (i)→N (i),如果g(i)=j使得任意一个顶点 v ′ ∈ N ( i ) v'\in N(i) v′∈N(i)和 g ( v ′ ) = u ′ g(v')=u' g(v′)=u′满足 h v ′ = h u ′ ) h_{v'}=h_{u')} hv′=hu′)称 S i S_i Si和 S j S_j Sj子树同构,记为: S i ≅ s u b t r e e S j S_i\cong{}_{subtree}S_j Si≅subtreeSj
之前的GNN利用了子树同构,graphSNN利用了重叠同构
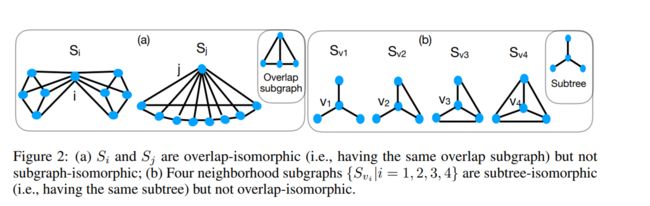
三种同构关系:子图同构>重叠同构>子树同构
作者提出一个定理:令M是一个GNN M和1-WL算法辨别非同构图的能力一样强大,如果M有足够的层数,且满足:每层的 S i S_i Si和 S j S_j Sj映射为两个不同的嵌入向量当且仅当他俩不是子树同构的。
这个定理提供了一个角度,为什么之前的GNN的性能上界是WL-test。因为一个好的GNN的映射就要满足 S i S_i Si和 S j S_j Sj映射为两个不同的嵌入向量当且仅当他俩不是子树同构这个条件。
之前的GNN都是用到了子树同构的条件,那么如果新的GNN结构用到了重叠同构,那么GNN的表达能力会不会有所提升呢?
消息传递框架GMP
作者提出了新的消息传递框架GMP,它可以根据重叠子图将局部结构注入到聚合方案中去。
一些前置定义:G中重叠子图集合: S ∗ = { S u v ∣ ( u v ) ∈ E } S^\ast=\{S_{uv}\vert(uv)\in E\} S∗={Suv∣(uv)∈E}
顶点v中的结构系数 ω : S ∗ S ∗ → R A u v = ω ( S v , S v u ) \omega:S*S^\ast\rightarrow R\;\;\;A_{uv}=\omega(S_v,S_{vu}) ω:S∗S∗→RAuv=ω(Sv,Svu)
这里的 ω ( ) \omega () ω()是是一个方程,这个方程用来刻画或描述顶点v和u的邻域关系。那么如何来设计呢?一个理想的函数应该满足以下条件:
1.Local closeness(局部紧密性): K i K_i Ki表示有i个顶点的完全图,如果 S v u = K i S_{vu}=K_i Svu=Ki, S v u ′ = K j S_{vu'}=K_j Svu′=Kj,则 ω ( S v , S v u ) > ω ( S v , S v u ′ ) \omega (S_v,S_{vu})>\omega (S_v,S_{vu'}) ω(Sv,Svu)>ω(Sv,Svu′)
2.Local denseness(局部稠密性):如果 S v u , S v u ′ S_{vu},S_{vu'} Svu,Svu′的顶点数和边数服从于 ∣ V v u ∣ = ∣ V v u ′ ∣ , ∣ E v u ∣ > ∣ E v u ′ ∣ |V_{vu}|=|V_{vu'}|,|E_{vu}|>|E_{vu'}| ∣Vvu∣=∣Vvu′∣,∣Evu∣>∣Evu′∣则 ω ( S v , S v u ) > ω ( S v , S v u ′ ) \omega (S_v,S_{vu})>\omega (S_v,S_{vu'}) ω(Sv,Svu)>ω(Sv,Svu′)
3.Isomorphic invariant(同构不变性):如果 S v u , S v u ′ S_{vu},S_{vu'} Svu,Svu′是同构的,那么 ω ( S v , S v u ) = ω ( S v , S v u ′ ) \omega (S_v,S_{vu})=\omega (S_v,S_{vu'}) ω(Sv,Svu)=ω(Sv,Svu′)

这是论文中给的例子
{{ }}是多重集
正则化的结构系数: A ~ v u = N o r m a l i z e ( ω ( S v , S v u ) ) \widetilde A_{vu}=Normalize(\omega (S_v,S_{vu})) A vu=Normalize(ω(Sv,Svu))
特征矩阵和顶点的特征向量: X ∈ R ∣ V ∣ ∗ f , x v ∈ R f X\in R^{\vert V\vert\ast f},x_v\in R^f X∈R∣V∣∗f,xv∈Rf
经过t层后的顶点特征: h v ( t ) , h v ( 0 ) = x v h_v^{(t)},h_v^{(0)}=x_v hv(t),hv(0)=xv
m a ( t ) = A G G R E G A T E N ( { { A ~ v u , h u ( t ) ∣ u ∈ N ( v ) } } ) m_a^{(t)}=AGGREGATE^N(\{\{\overset{}{\widetilde A_{vu},h_u^{(t)}\vert u\in N(v)}\}\}) ma(t)=AGGREGATEN({{A vu,hu(t)∣u∈N(v)}})
m v ( t ) = A G G R E G A T E N ( { { A ~ v u ∣ u ∈ N ( v ) } } ) h u ( t ) m_v^{(t)}=AGGREGATE^N(\{\{\overset{}{\widetilde A_{vu}\vert u\in N(v)}\}\})h_u^{(t)} mv(t)=AGGREGATEN({{A vu∣u∈N(v)}})hu(t)
h v ( t + 1 ) = C O M B I N E N ( m v ( t ) , m a ( t ) ) h_v^{(t+1)}=COMBINE^N(m_v^{(t)},m_a^{(t)}) hv(t+1)=COMBINEN(mv(t),ma(t))
GraphSNN具体实现
如何设计 ω ( S v , S v u ) \omega(S_v,S_{vu}) ω(Sv,Svu)函数?,作者是这么写的
ω ( S v , S v u = ∣ E v u ∣ ∣ V v u ∣ ⋅ ∣ V v u − 1 ∣ ∣ V v u ∣ λ \omega(S_v,S_{vu}=\frac{\vert E_{vu}\vert}{\vert V_{vu}\vert\cdot\vert V_{vu}-1\vert}\vert V_{vu}\vert^\lambda ω(Sv,Svu=∣Vvu∣⋅∣Vvu−1∣∣Evu∣∣Vvu∣λ
这里的 λ \lambda λ是一个超参数
h v ( t + 1 ) = M L P θ ( γ ( t ) ( ∑ u ∈ N ( v ) A ~ v u + 1 ) h v ( t ) + ∑ u ∈ N ( v ) ( A ~ v u + 1 ) h u ( t ) ) h_v^{(t+1)}=MLP_\theta(\gamma^{(t)}(\sum_{u\in N(v)}{\widetilde A}_{vu}+1)h_v^{(t)}+\sum_{u\in N(v)}({\widetilde A}_{vu}+1)h_u^{(t)}) hv(t+1)=MLPθ(γ(t)(∑u∈N(v)A vu+1)hv(t)+∑u∈N(v)(A vu+1)hu(t))
其中, γ ( t ) \gamma^(t) γ(t)是可学习的参数
实验
GraphSNN做了两种实验,在很多数据集上都跑了,得出来非常不错的效果。
Node classification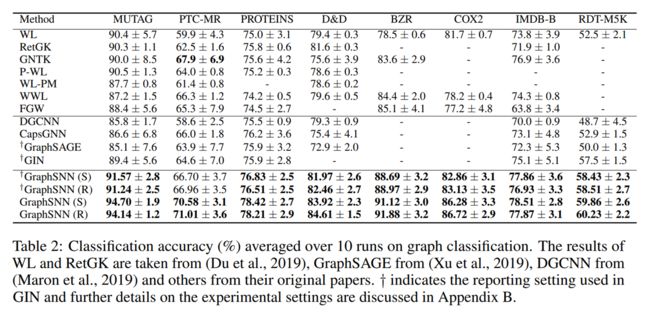
他这里的图例可能有点错误,不是graph classification,是node classification
我觉得这里很厉害的地方是,他每一个数据集都运行了10次以上,取平均值,在每个task上还详细说明了自己的运行超参,以及自己训练数据,验证数据,测试数据的分类。属于是对自己的模型非常有自信了。
graph classification
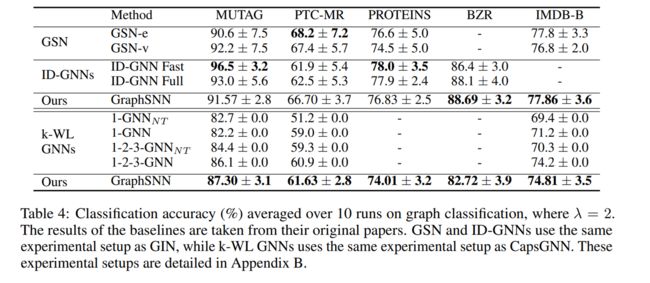
图分类任务上效果也还不错,也是运行10次取平均,训练参数也是很详尽的写在论文里,感兴趣的读者可以自己去看论文
over smoothing问题
这里我还想在关注一下GraphSNN的过平滑问题,论文里面也就这个问题有一点实验和讨论

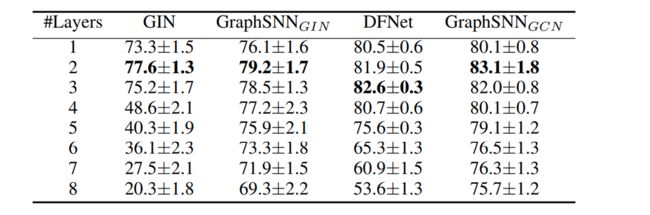
这两张图是作者在Cora数据集上做的实验,和GCN,GIN做比较,从这两张图我们可以得到这样一些信息。
1.GNN的深度现在还不是很深,太深的GNN他的准确率反而会下降,而且会下降得非常厉害,这个就是over smoothing问题。
2.GraphSNN在加了layer数之后精度也会下降,并不能真正的解决over smoothing问题。但是可以缓解这个问题,而且他的精度下降并不是很大,可扩展性比较好。
总结
最近在看一些图神经网络的顶会文章,发现GNN这个领域并没有定式,比如说像nlp的transformer结构,cv领域的CNN这种经典架构,这段时间看的Graphormer,这篇的GraphSNN,还有看了但是没做笔记的NAFS(一种无参数的representation learning)貌似都比较厉害,也是百家争鸣的局面。但是总感觉进展不大。文章链接放在低下,有想进一步深入的读者自取
NAFS
GraphSNN
Graphormer