主成分分析法（PCA）的理解（附python代码案例）

最近在文献调研，发现PCA基本都有用到，回忆起了机器学习和数学建模，总之还是要好好学学捏。

一、PCA简介

定义：主成分分析（Principal Component Analysis, PCA）是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

换一种说法：PCA去除噪声和不重要的特征，将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息，而且可以提升数据处理的速度。

为什么会出现PCA呢？因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。在用统计方法研究多变量问题时，变量太多会增加计算量和分析问题的复杂性。

核心思想：降维，这个过程中可能会损失精度，但是能获取更高更关键的因素。

---

二、举个例子

例子1：评选三好学生，每个学生都有很多特征，比如学习成绩、社会实践、思想道德、体育成绩等。在评比中，有一些特征属于“ 无用特征 ”，比如身高、体重、头发长短等，这些特征在评比中是不会考虑的；而有一些特征属于“ 冗余特征 ”，比如各科成绩、总成绩、GPA，实际上这些有一个即可。

例子2：见下图。原本黑色坐标系中需要记录每个点的横纵坐标(xi, yi)，也就是 2 个纬度的数据。

但如果转换坐标系，如绿色坐标系所示，让每个点都位于同一条轴上，这样每个点坐标为(xi’, 0)，此时仅用x’坐标表示即可，即 1 个维度。

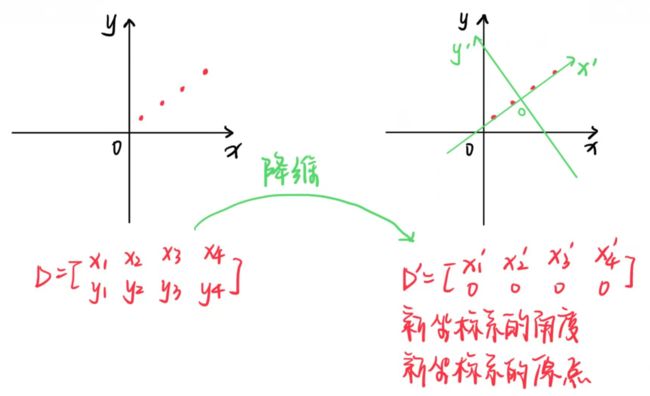
在这个过程中，原先需要保存的 2 维数据变成了 1 维数据，叫做数据降维 / 数据提炼。而PCA的任务形象理解也就是坐标系的转换。

PCA其实目的就是寻找这个转换后的坐标系，使数据能尽可能分布在一个或几个坐标轴上，同时尽可能保留原先数据分布的主要信息，使原先高维度的信息，在转换后能用低维度的信息来保存。而新坐标系的坐标轴，称为主成分(Principal components, PC)，这也就是PCA的名称来源。

---

三、计算过程（公式）

3.0 题干假设

首先假设有 n 个样本，p 个特征，$x_{ij}$ 表示第i个样本的第 j 个特征，这些样本构成的 n × p 特征矩阵 X 为：
$$X=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1p}\\ x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]=[x_1,x_2,\cdots ,x_p]$$

我们的目的是找到一个转换矩阵，将 p 个特征转化为 m 个特征（m < p），从而实现特征降维。即找到一组新的特征 / 变量$z_1$, $z_2$, …, $z_m$（m ≤ p），满足以下式子：
$$\{\begin{array}{l}\begin{array}{rl}{z}_1& =l_{11}{x}_1+l_{12}{x}_2+\cdots +l_{1p}{x}_p\\ z_2& =l_{21}{x}_1+l_{22}{x}_2+\cdots +l_{2p}{x}_p\\ ⋮& \\ z_m& =l_{m1}{x}_1+l_{m2}{x}_2+\cdots +l_{mp}{x}_p\end{array}\end{array}$$

3.1 标准化

有的博客写的是去中心化而不是标准化，在计算过程中也仅体现出步骤的不同，实际两种方法都可以用的，大家也可以看看这篇博客看看这几种“化”的区别：数据归一化、标准化和去中心化。本篇只研究标准化，第四部分的参考链接中介绍了标准化和去中心化的步骤，写得很详细，欢迎大家学习~

标准化过程如下：

1. 计算每个特征（共p个特征）的均值 $\overline{x_j}$ 和标准差 $S_j$，公式如下：
   $$\overline{x_j}=\frac{1}{n}\sum _{i=1}^n{x}_{ij}$$
   $$S_j=\sqrt{\frac{{\sum }_{i=1}^n(x_{ij}-\overline{x_j}{)}^2}{n-1}}$$

2. 将每个样本的每个特征进行标准化处理，得到标准化特征矩阵$X_{stand}$：
   $$X_{ij}=\frac{x_{ij}-\overline{x_j}}{S_j}$$
   $$X_{stand}=\left[\begin{array}{cccc}{X}_{11}& X_{12}& \cdots & X_{1p}\\ X_{21}& X_{22}& \cdots & X_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ X_{n1}& X_{n2}& \cdots & X_{np}\end{array}\right]=[X_1,X_2,\cdots ,X_p]$$

3.2 计算协方差矩阵

协方差矩阵是汇总了所有可能配对的变量间相关性的一个表。

协方差矩阵 R 为：
$$R=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1p}\\ r_{21}& r_{22}& \cdots & r_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ r_{p1}& r_{p2}& \cdots & r_{pp}\end{array}\right]$$

$$\begin{array}{rl}{r}_{ij}& =\frac{1}{n-1}\sum _{k=1}^n(X_{ki}-\overline{X_i})(X_{kj}-\overline{X_j})\\ & =\frac{1}{n-1}\sum _{k=1}^n{X}_{ki}{X}_{kj}\end{array}$$

3.3 计算特征值和特征值向量

计算矩阵R的特征值，并按照大小顺序排列，计算对应的特征向量，并进行标准化，使其长度为1。R是半正定矩阵，且$tr(R)={\sum }_{k=1}^p{\lambda }_k=p$。

特征值：${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_p\ge 0$

特征向量：$L_1=[l_{11},l_{12},\dots ,l_{1p}{]}^T\dots L_p=[l_{p1},l_{p2},\dots ,l_{pp}{]}^T$

3.3 多重共线性检验（可跳过）

若存在明显的多重共线性，则重新根据研究问题选取初始分析变量。

多重共线性的影响、判定及消除的方法

由于这里是【计算过程】而不是【研究过程】，此处不推翻3.0部分的假设，着重探讨PCA的计算流程即可，故3.3和3.4部分可跳过，真正的研究过程再考虑特征矩阵如何取。

3.4 适合性检验（可跳过）

一组数据是否适用于主成分分析，必须做适合性检验。可以用球形检验和KMO统计量检验。

1. 球形检验（Bartlett）
球形检验的假设：
H0：相关系数矩阵为单位阵（即变量不相关）
H1：相关系数矩阵不是单位阵（即变量间有相关关系）

2. KMO（Kaiser-Meyer-Olkin）统计量
KMO统计量比较样本相关系数与样本偏相关系数，它用于检验样本是否适于作主成分分析。KMO的值在0-1之间，该值越大，则样本数据越适合作主成分分析和因子分析。一般要求该值大于0.5，方可作主成分分析或者相关分析。Kaiser在1974年给出了经验原则：

KMO值的范围	适合性情况
0.9以上	适合性很好
0.8~0.9	适合性良好
0.7~0.8	适合性中等
0.6~0.7	适合性一般
0.5~0.6	适合性不好
0.5以下	不能接受的

3.5 计算主成分贡献率及累计贡献率

第 i 个主成分的贡献率为：
$$\frac{{\lambda }_i}{{\sum }_{k=1}^p{\lambda }_k}$$

前 i 个主成分的累计贡献率为：
$$\frac{{\sum }_{j=1}^i{\lambda }_j}{{\sum }_{k=1}^p{\lambda }_k}$$

3.6 选取和表示主成分

一般取累计贡献率超过80%的特征值所对应的第一、第二、…、第m（m ≤ p）个主成分。Fi表示第i个主成分：
$$F_i=l_{i1}{X}_1+l_{i2}{X}_2+\cdots +l_{ip}{X}_p,(i=1,2,\dots ,p)$$

3.7 系数的简单分析

对于某个主成分而言，指标前面的系数越大（即 $l_{ij}$），代表该指标对于该主成分的影响越大。

---

四、案例分析（python）

参考了这个链接：主成分分析（PCA）及其可视化——python。其中提供了两种方法，分别对应3.1为标准化和去中心化的步骤，每一步都有注释和代码，很详细！

还有这个写的太好了qaq，英文的球球大家一定要看：Principal Component Analysis in 3 Simple Steps

4.1 一步一步PCA

1. 数据集
是从这部分的第一个链接里随便扣出来的部分数据，如果大家感兴趣可以玩玩。

链接：https://pan.baidu.com/s/108JPN6LGg7GJfxCiJaItZA
提取码：3w5u

2. 安装库

pip install pandas
pip install numpy
pip install seaborn
pip install matplotlib
pip install sklearn
pip install factor_analyzer

3. 读取数据集

import pandas as pd
import numpy as np
import seaborn as sns
# 读取数据集
df = pd.read_csv(r"D:\vscpro\PyThon\data.csv",
     sep=',',
     header=None).reset_index(drop=True)
df.columns = ['a', 'b', 'c']
df.dropna(how="all", inplace=True)
df.tail()

4. 适合性检验（Bartlett && KMO）

from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
from factor_analyzer.factor_analyzer import calculate_kmo

df_check = df
# Bartlett 球状检验 
chi_square_value, p_value = calculate_bartlett_sphericity(df_check)
print("Bartlett=", chi_square_value, p_value)

# KMO检验(>0.5为好，越靠近1越好)
kmo_all, kmo_model = calculate_kmo(df_check)
print("KMO=", kmo_all)

5. 标准化

# 标准化
from sklearn import preprocessing
from sklearn.preprocessing import StandardScaler
X = df.iloc[:, 0:3].values
Y = df.iloc[:, 2].values
X_std = StandardScaler().fit_transform(X)

df = preprocessing.scale(df)
print(df)

6. 法一：计算系数相关矩阵并特征求解
金融领域常使用相关矩阵代替协方差矩阵。

# 系数相关性矩阵
covX = np.around(np.corrcoef(df.T), decimals = 3)
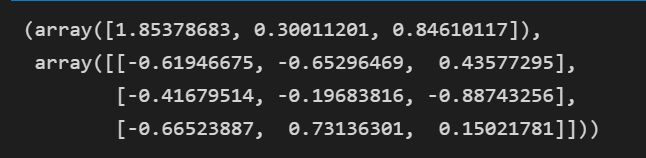
# 系数相关矩阵特征求解
featValue, featVec=  np.linalg.eig(covX.T)
print(featValue, featVec)

7. 法二：计算协方差矩阵并特征求解

# 协方差矩阵
# ①写法：
# mean_vec = np.mean(X_std, axis=0)
# covX = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
# ②写法：
covX = np.cov(X_std.T)
# print(covX)

# 协方差矩阵特征求解
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)

# 基于相关矩阵的标准化数据的特征分解
cor_mat1 = np.corrcoef(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cor_mat1)

# 基于相关矩阵的原始数据的特征分解
cor_mat2 = np.corrcoef(X.T)
eig_vals, eig_vecs = np.linalg.eig(cor_mat2)
print(eig_vals, eig_vecs)

8. 计算贡献率

# 特征值排序输出
featValue = sorted(featValue)[::-1]

# 贡献度
gx = featValue / np.sum(featValue)

#累计贡献度
lg = np.cumsum(gx)
print(featValue, gx, lg)

9. 选取主成分

# 选取主成分，一般要超过80%或85%
k = [i for i in range(len(lg)) if lg[i] < 0.85]
k = list(k)
print(k)

10. 表示主成分

# 主成分对应的特征向量矩阵
selectVec = np.matrix(featVec.T[k]).T
selectVe = selectVec*(-1)
print(selectVec)

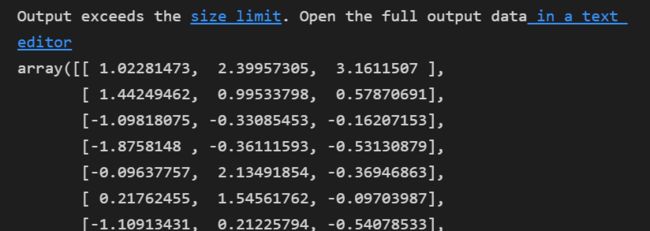
# 表示主成分
finalData = np.dot(X_std, selectVec)
print(finalData)

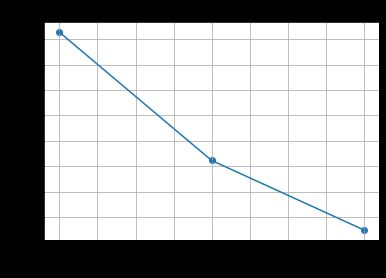
11. 绘制图像

import matplotlib.pyplot as plt
# 绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), featValue)
plt.plot(range(1, df.shape[1] + 1), featValue)

plt.title("Plot")  
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")
 
plt.grid()
plt.show()

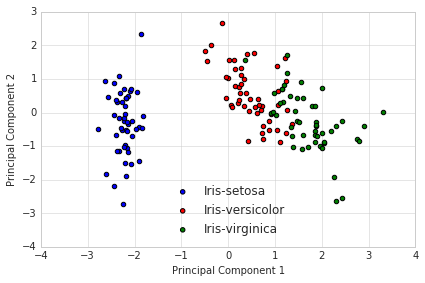
4.2 sklearn的PCA

这个数据集是经典鸢尾花~

from sklearn.decomposition import PCA as sklearnPCA
sklearn_pca = sklearnPCA(n_components=2)
Y_sklearn = sklearn_pca.fit_transform(X_std)

# draw
with plt.style.context('seaborn-whitegrid'):
    plt.figure(figsize=(6, 4))
    for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
        plt.scatter(Y_sklearn[y==lab, 0],
                    Y_sklearn[y==lab, 1],
                    label=lab,
                    c=col)
    plt.xlabel('Principal Component 1')
    plt.ylabel('Principal Component 2')
    plt.legend(loc='lower center')
    plt.tight_layout()
    plt.show()

4.3 其他实现代码（长期更新）

这部分用来堆堆其他大佬们写的代码，方便后面学习和使用。

4.3.1 numpy实现和sklearn实现

来自主成分分析（PCA）原理详解

（1）PCA的Python实现

##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want
  #mean of each feature
  n_samples, n_features = X.shape
  mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
  #normalization
  norm_X=X-mean
  #scatter matrix
  scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
  #Calculate the eigenvectors and eigenvalues
  eig_val, eig_vec = np.linalg.eig(scatter_matrix)
  eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
  # sort eig_vec based on eig_val from highest to lowest
  eig_pairs.sort(reverse=True)
  # select the top k eig_vec
  feature=np.array([ele[1] for ele in eig_pairs[:k]])
  #get new data
  data = np.dot(norm_X,np.transpose(feature))
  return data

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])

print(pca(X,1))

（2）sklearn的PCA

##用sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=1)pca.fit(X)
print(pca.transform(X))

---

五、补充总结

PCA的数学思想：

• 根据p个特征的线性组合，得到一个新的特征z，使得该特征的方差最大，该特征即为主成分。
• 再次寻找p个特征的线性组合，得到新的特征，该特征与之前得到的主成分线性无关，且方差最大。

其余要点：

• 如果每个主成分的贡献率都相差不多，则不建议使用PCA。因为它一定程度上舍弃了部分信息，来提高整体的计算效率。
• 对于降维形成的主成分，我们经常无法找到其在实际情况中所对应的特征，即主成分的解释其含义一般带有模糊性，不像原始变量的含义那么清楚确切，这也是PCA的缺陷所在。
• PCA不可用于评价类模型。可用于聚类、回归，如回归分析解决多重共线性。

---

六、参考链接

1. 如何理解主成分分析法 （PCA）
2. 清风数学建模学习笔记——主成分分析(PCA)原理详解及案例分析
3. PCA的数学原理
4. 【数据处理方法】主成分分析（PCA）原理分析
5. 协方差矩阵和矩阵相关系数的理解