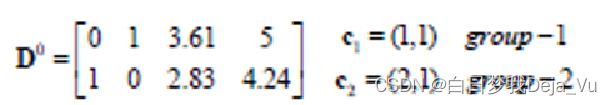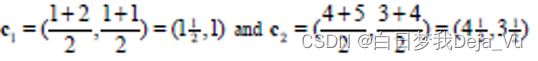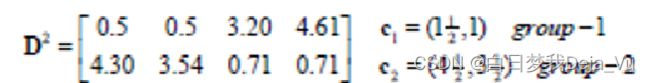机器学习-K-means聚类算法
聚类算法一般分为三种，分别是基于划分的聚类、基于密度的聚类、层次的聚类，笔者这边介绍的是其中最常见的一种基于划分的聚类，即K-means聚类算法。本文是学习《机器学习算法基础-覃秉丰》所做的一些笔记和补充。
1、聚类和分类的区别
分类算法的样本是带标签的，聚类算法的样本是不带标签的，试先并不知道这个数据集是属于哪一个类别，根据数据的特征来给数据进行聚类，并且聚类是无监督学习而分类是属于有监督学习的。
2、K-means算法的介绍
参数K：K-means算法与KNN算法都有个K，但是两个算法的K是不一样的，K-means中的参数K值指的是将事先输入的n个数据对象划分为k个聚类（簇），以便使得所获得的聚类满足：同一个聚类中的对象相似度较高；而不同聚类中的对象相似度较小。
算法思想：以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果
3、K-means算法实现过程
- 先从没有标签的元素集合A中随机选取k个元素，作为 k个子集各自的重心，即先定义总共有多少个类/簇。
- 分别计算剩下的元素到k个子集重心的距离（这里的距离也可以使用欧氏距离），根据距离将这些元素分别划归到最近的子集。
- 根据聚类结果，重新计算重心（重心的计算方法是计算子集中所有元素各个维度的算数平均数）。
- 将集合A中全部元素按照新的重心然后再重新聚类。
- 不停的重复上述操作，直到聚类结果不再发生变化。
4、K-means算法示例
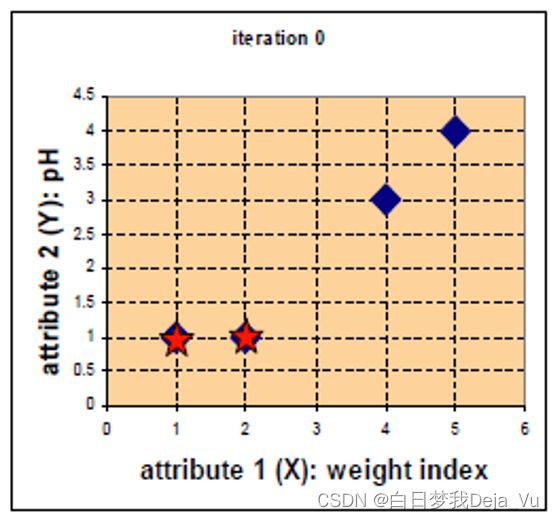
在坐标轴中有四个点，分别记作A(1,1)，B(2,1)，C(4,3)，D(5,4)，对这四个点来进行聚类操作，假设选取(1,1)、(2,1)为两个分类中心点。如下图所示。
首先分别计算A、B、C、D四个点分别到分类中心点的距离，如下图矩阵D0所示。D0矩阵中第一行为各个点到第一个分类中心点距离，第二行为各个点到第二个分类中心点的距离
计算得出D0矩阵之后，比较各个点到分类中心点的距离大小，并将各个点分类到距离其较近的那个点处。得到矩阵G0。如下图所示。
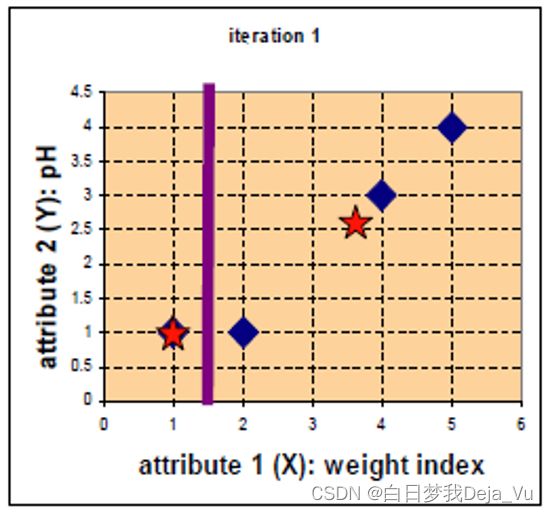
再分别计算新的一轮的两类中心点。根据该矩阵我们可以得到group-1中只有A点本身，所以group-1的分类中心点没有变化。而group-2中有B、C、D三个点，所以重新计算得到新的group-2的分类中心点。
之后开始新的一轮的迭代，操作和上述操作一致。
计算各个点到新一轮的中心点的距离结果如图矩阵D1所示：
得到的新的分类情况如图G1所示：
再根据新的分类情况计算下一轮的分类中心点
再进行第三轮分类
计算各个点到新一轮的中心点的距离结果如图矩阵D2所示：
得到的新的分类情况如图G2所示：
此时发现聚类结果没有发生变化，算法迭代停止。因此K-means聚类算法的结果就是将这四个点分成了A、B和C、D两类。
5、Mini Batch K-Means
Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间。这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，结果一般只略差于标准算法。
该算法的迭代步骤有两步 :
- 从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心。
- 更新质心与K均值算法相比，数据的更新是在每一个小的样本集上。Mini Batch K-Means比K-Means有更快的收敛速度，但同时也降低了聚类的效果，但是在实际项目中却表现得不明显。
由聚类的结果我们也可以发现，Mini Batch K-Means的效果和K-means的效果差不多
6、K-means算法的缺点
1、对k个初始质心的选择比较敏感，容易陷入局部最小值。例如，我们上面的算法运行的时候，有可能会得到不同的结果，如下面这两种情况。K-means也是收敛了，只是收敛到了局部最小值。
2、k值的选择是用户指定的，不同的k得到的结果会有挺大的不同，如下图所示，左边是k=3的结果，蓝色的簇太稀疏了，蓝色的簇应该可以再划分成两个簇。右边是k=5的结果，红色和蓝色的簇应该合并为一个簇。
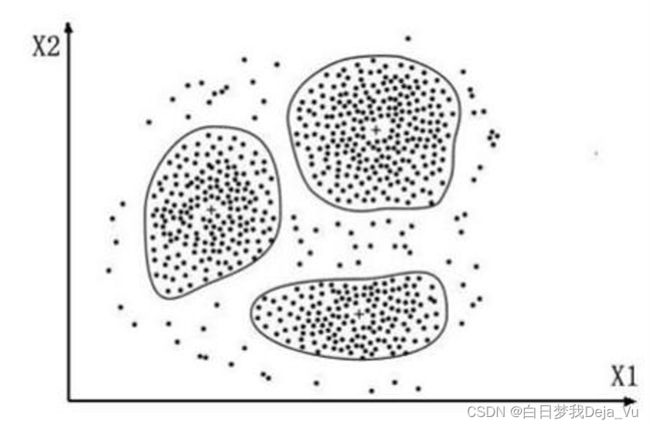
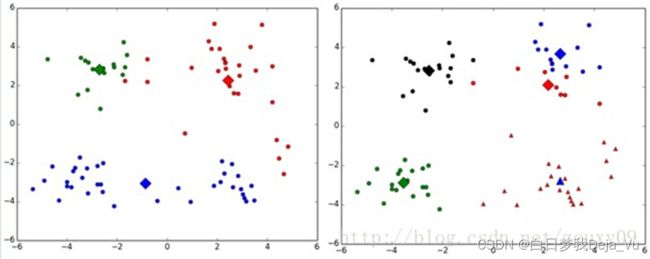3、存在局限性，如下图这种非球状的数据分布就搞不定了，按照笔者的想法，最后的分类结果应该如图1所示，但是我们使用K-means聚类算法之后出现的反而是第二种结果。
7、K-means聚类算法可视化
Visualizing K-Means Clustering（可视化网站）
在该网站中我们可以随便定义参数K并且可以清晰的看到每次聚类的结果
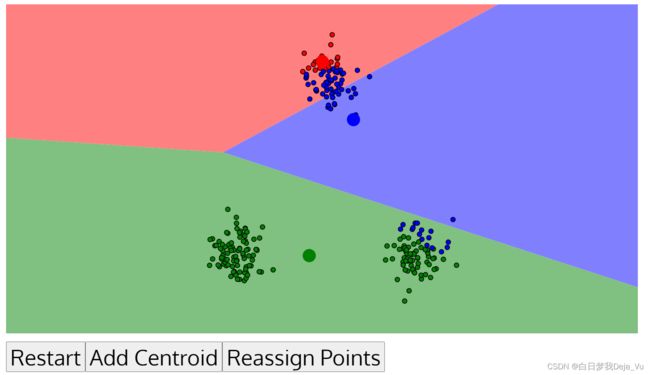
当我们选择其中一个来进行实验时，可以看一下效果，如下图所示，我们看出最后按我们的理想化的话，最后的分类结果应该是三类，因此这边选取了参数K为3，然后不断的进行迭代操作。
最后聚类结果如下图所示，此时聚类不发生变化，算法的迭代停止。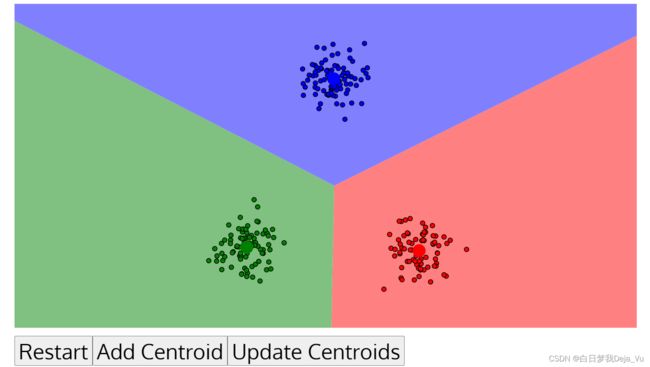
这边再给大家看一个K-means聚类效果很差的例子
像这样的笑脸样本， 我们最后的结果应该是按两个眼睛，然后嘴巴，然后是外面的一圈。分类成四种簇，但是当我们使用K-means算法时出现的效果就很差。如下图所示。
这个时候我们应该使用基于密度的聚类方法，比如DBSCAN算法，使用DBSCAN算法的结果如下图所示。
