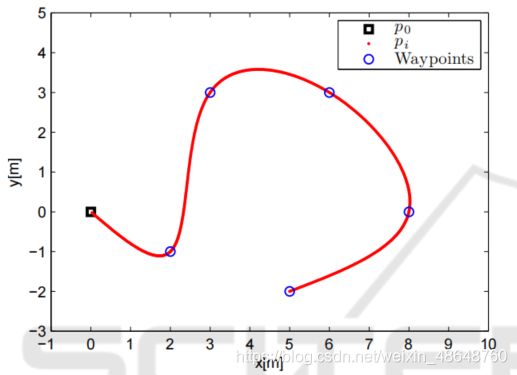
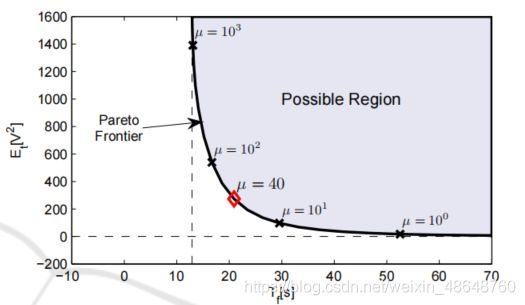
- 简单介绍物联网MQTT协议
Zio_Zhou
计算机网络linux
在学习mqtt应用层协议之前,我们先来介绍一下发布/订阅模型以及请求/响应模型两种模型。请求/响应模型是网络应用系统中最常见的模型。在这种模型中,一个客户端(如一个Web浏览器)向服务器发送一个请求,服务器处理这个请求并返回一个响应。这个过程是同步的,意味着客户端需要等待服务器的响应。这种模型的优点是简单和易于理解,但在处理大量并发请求时可能会导致性能问题。发布/订阅模型。在这种模型中,有一个或多
- VB.NET,C#字典对象来保存用户数据,支持大小写
专注VB编程开发20年
java开发语言
用这个保存的,登录时大小写不一样会不会无法识别根据你提供的SaveUsersToJson方法,我注意到你使用了JSON序列化来保存用户数据,但没有显式指定字典的比较器。这意味着在反序列化时,默认会使用区分大小写的比较器,导致大小写不同的用户名无法正确匹配。问题分析当你保存用户数据时:PrivateSubSaveUsersToJson(usersAsDictionary(OfString,UserI
- 疲劳检测与行为分析:工厂智能化实践
智驱力人工智能
安全智慧城市行为识别人员属性识别疲劳检测抽烟检测徘徊检测
视觉分析算法赋能工厂疲劳与安全管理一、背景与需求在制造业中,疲劳作业是导致安全事故和效率下降的核心因素之一。传统人工巡检存在覆盖面不足、响应滞后等问题,而基于视觉分析的智能监控系统通过多算法协同,可实现全天候、高精度的疲劳检测与行为管理。本文围绕疲劳检测算法、人员计数算法、抽烟检测算法及徘徊检测算法,探讨其在工厂场景中的技术实现与应用价值。二、技术实现疲劳检测算法原理:基于PERCLOS(眼睑闭合
- 【开源项目】「安卓原生3D开源渲染引擎」:Sceneform‑EQR
「安卓原生3D开源渲染引擎」:Sceneform‑EQR渲染引擎“那一夜凌晨3点,第一次提交PR的手在抖……”——我深刻体会这种忐忑与激动。仓库地址:(github.com)。一、前言:开源对我意味着什么DIY的自由Vs.工业化的束缚刚入Android原生开发时,我习惯自己在项目里嵌入各种3D渲染/AR/XR模块,结构臃肿、流程混乱。当我知道GoogleSceneformSDK被弃用,起初只是出于
- 潜入思维的海洋:SoftCoT++如何让语言模型更聪明
步子哥
智能涌现语言模型人工智能自然语言处理
在人工智能的浩瀚星空下,大型语言模型(LLMs)如同一颗颗璀璨的恒星,照亮了从文本生成到复杂推理的广阔领域。然而,这些模型在推理任务中往往像是在迷雾中航行——尽管它们能抵达目的地,却常常因为固定的思维路径而错过更优的航线。2025年5月,一篇题为《SoftCoT++:Test-TimeScalingwithSoftChain-of-ThoughtReasoning》的论文如同一盏明灯,照亮了如何让
- BI+AI实战:我们如何用3秒完成车企供应链推演
qq_43696218
人工智能
一、BI+AI引领财务分析新纪元在财务数据分析领域,奥威BI+AI正以革命性的姿态颠覆传统。当金蝶、用友等工具仍深陷报表泥潭时,奥威BI+AI通过深度融合商业智能(BI)与人工智能(AI),实现了从滞后报表到实时洞察的飞跃。这不仅极大地提升了财务分析的效率,更为企业的战略决策提供了前所未有的精准支持。二、BI+AI的核心技术优势实时动态分析o奥威BI+AI摒弃了静态数据集,依托原始科目余额表实
- 技术调研:时序数据库(一)
myskybeyond
时序数据库时序数据库数据库
选择时序数据库时,选择当下主流的解决方案。目前主流的开源解决方案有InfluxDB、TDengine和TimescaleDB。下文从多个维度对比分析,最终根据需求做出选型决策。1.核心架构与设计理念数据库架构特点核心优势InfluxDB-专为时序数据设计的分布式数据库-基于时间线(TimeSeries)模型-开源版(OSS)与商业版(Cloud/Enterprise)功能差异大高写入吞吐量、原生支
- 鞋履智造的“隐形工匠”:PROFIBUS DP转ETHERNET/IP网关应用实践
在鞋履制造产线中,西门子PLC凭借PROFIBUSDP协议实现精准逻辑控制,而涂胶机器人多采用ETHERNET/IP协议执行鞋面粘合与处理任务。为实现设备高效协同,JH-PB-EIP疆鸿智能PROFIBUSDP转ETHERNET/IP网关化身“通信中枢”,破解协议壁垒,成为提升鞋子舒适度与耐用性的核心助力。硬件连接时,需先在西门子PLC中完成DP从站组态,设定地址并通过专用电缆接入网关DP端口,针
- 【linux】yum工具篇
nanguochenchuan
Linux操作系统linux运维服务器
Yum工具概述Yum(YellowdogUpdaterModified)是RedHat系列Linux发行版(如CentOS、Fedora)中最核心的软件包管理工具,它基于RPM包管理系统构建,通过自动解决依赖关系极大简化了软件管理流程。与直接使用rpm命令相比,Yum能自动处理软件包依赖,让系统管理员从"依赖地狱"中解脱出来。Yum工作原理深度解析Yum的工作流程可分为四个关键阶段:仓库配置读取:
- Linux tcp_info:监控TCP连接的秘密武器
CodeWithMe
网络linuxtcp/ip
深入解析Linuxtcp_info:TCP状态的实时监控利器在开发和运维网络服务时,我们常常遇到这些问题:我的TCP连接为什么速度慢?是发生了重传,还是窗口太小?拥塞控制到底有没有生效?这些问题的答案,其实隐藏在内核的tcp_info结构中。本文将详细介绍:tcp_info是什么,怎么用?各字段含义和实际用途在调优TCP服务中的应用实践一、什么是tcp_info?tcp_info是Linux内核中
- 深度解析JavaScript 闭包
coding随想
JavaScriptjavascript开发语言ecmascript
深度解析JavaScript闭包引言:为什么闭包让人又爱又怕?在JavaScript的学习过程中,闭包(Closure)是一个绕不开的“坎”。很多开发者第一次接触闭包时,会感到一头雾水:“为什么函数能记住外部作用域的变量?”、“为什么闭包会导致内存泄漏?”。但另一方面,闭包又是JavaScript最强大的特性之一,它支撑着模块化开发、数据封装、异步编程等核心场景。本文将通过通俗的语言和生动的案例,
- 【Linux】ghb工具
nanguochenchuan
Linux操作系统linux运维服务器
GDB简介GDB(GNUDebugger)是Linux系统中最强大的命令行调试工具,由GNU项目开发。作为程序员调试C/C++程序的利器,GDB能帮助你:定位程序崩溃原因分析程序运行状态跟踪变量值变化检测内存错误安装与配置安装方法#Ubuntu/Debiansudoaptinstallgdb#CentOS/RHELsudoyuminstallgdb#ArchLinuxsudopacman-Sgdb
- Vue SPA 路由跳转无法回到顶部问题排查与解决
浪裡遊
vue.jsjavascriptecmascriptpiniarouterhtml
VueSPA路由跳转无法回到顶部问题排查与解决1.问题现象描述在使用Vue3+VueRouter4开发单页应用(SPA)时,遇到如下问题:点击导航栏或页脚的路由跳转后,页面没有自动回到顶部。即使配置了VueRouter的scrollBehavior,页面依然没有回到顶部的效果。有时内容会被导航栏遮住,看起来像"没有回到顶部"。2.常见原因分析内容区没有为导航栏预留空间导航栏是fixed或stick
- 期货反向跟单-亏损原因(四)主观误判行情
反向跟单策略
期货反向跟单区块链大数据数据分析人工智能
熟悉期货反向跟单策略的运营者都清楚,它宛如一把双刃剑,在单边行情中锋芒毕露,能轻松斩获丰厚利润;但一旦遭遇震荡行情,便如同陷入泥潭,可能面临持续亏损的局面。造成这种局面的关键,在于盘手的交易习惯。震荡行情下,价格来回波动,盘手在亏损时往往会选择扛单,即便亏损也能扛到盈利。期货市场的走势难以捉摸,大行情并非每日可见,震荡才是市场的常态之一。特别是在缺乏重大国际事件或基本面消息刺激时,市场陷入长达一个
- webpack和vite对比解析(AI)
秉承初心
AI创造webpack前端node.js
以下是Webpack和Vite的对比解析,从核心机制、性能、配置扩展性、适用场景等维度进行详细说明:⚙️一、核心机制差异构建模式Webpack:采用打包器模式,启动时需遍历整个模块依赖图,将所有资源打包成Bundle,再启动开发服务器。Vite:基于ESModules原生支持,开发环境跳过打包,按需编译(浏览器请求时实时编译)。生产环境才用Rollup打包。依赖处理Webpack:冷启动时需全量打
- 将图片的base64编码直接嵌入到html文件的css中
Kuo-Teng
软件开发实战htmlcssjavascript
将图片的base64编码直接嵌入到html文件的css中1.背景2.将图片进行base64编码3.将图片的base64编码写入到css1.背景如果你需要在html中引入一张外部图片,你可能会这样做:如果你将引用的图片保存到本地,你可能会这样做:但是,如果网络延迟较高,或者在jar包中运行Java项目时无法根据路径顺利找到图片呢?那么,将图片的base64编码直接写入html文件便是最好的选择!2.
- 【为什么网络安全缺口很大,而招聘却很少?】
网络安全工程师教学
安全黑客技术网络安全web安全网络安全游戏数据库
为什么网络安全缺口很大,而招聘却很少?2020年我国网络空间安全人才数量缺口超过了140万,就业人数却只有10多万,缺口高达了93%。这里就有人会问了:1、网络安全行业为什么这么缺人?2、明明人才那么稀缺,为什么招聘时招安全的人员却没有那么多呢?首先来回答第一个问题,从政策背景、市场需求、行业现状来说。政策背景自从斯诺登棱镜门事件曝光之后,网络空间站成为现代战场第一战场,网络安全能力也被各国列为了
- Webpack和Vite的区别
棋丶
webpack前端node.js
一、构建速度方面webpack默认是将所有模块都统一打包成一个js文件,每次修改都会重写构建整个项目,自上而下串行执行,所以会随着项目规模的增大,导致其构建打包速度会越来越慢vite只会对修改过的模块进行重构,构建速度比webpack快得多二、开发效率在开发时,因为webpack会将所有模块都统一进行打包,然后再在浏览器中进行热更新,导致每次更新都需要重构项目,会造成很长的等待时间vite是在浏览
- API测试(一):PortSwigger靶场笔记
h4ckb0ss
笔记网络安全web安全
写在前面这篇文章是关于作者在学习PortSwigger的APITest类型漏洞时的记录和学习笔记使用到的工具为BurpSuitePro漏洞简介什么是apiAPI全称为ApplicationInterface,是应用程序对外提供功能的接口,现在主要有三种api风格,分别是JSON风格的api,RESTful风格的api以及Graphic风格的apiJSON风格请求获取用户信息POST/api/get
- 使用CSS和HTML实现3D图片环绕效果
码力无边-OEC
csshtml3dweb前端
使用CSS和HTML实现3D图片环绕效果在本篇博客中,将介绍如何使用HTML和CSS实现一个3D图片环绕效果。这个效果不仅具有视觉吸引力,而且具有高度的互动性,鼠标悬停时动画会暂停。接下来将一步步讲解这个效果的实现过程。1.效果2.页面结构与布局首先,我们来看一下HTML的基本结构。该效果的核心是一个元素,它包含了多个图片的,每个div中都设置了不同的背景图片。HTML代码:3D图片环绕效果</
- Node.js特训专栏-实战进阶:8. Express RESTful API设计规范与实现
爱分享的程序员
Node.jsjavascriptnode.js前端
欢迎来到Node.js实战专栏!在这里,每一行代码都是解锁高性能应用的钥匙,让我们一起开启Node.js的奇妙开发之旅!Node.js特训专栏主页专栏内容规划详情ExpressRESTfulAPI设计规范与实现:构建标准化、可维护的接口服务在前后端分离架构盛行的今天,RESTfulAPI已成为Web服务交互的事实标准。基于Express框架构建RESTfulAPI,既能利用Node.js的高效性能
- 网站策划书通用模板
程序员小郑1024
项目策划专区java编程语言大数据
网站策划书通用模板一个网站的成功与否与建站前的网站策划有着极为重要的关系。在建立网站前应明确建设网站的目的,确定网站的功能,确定网站规模、投入费用,进行必要的市场分析等。只有详细的策划,才能避免在网站建设中出现的很多问题,使网站建设能顺利进行。网站策划是指在网站建设前对市场进行分析、确定网站的目的和功能,并根据需要对网站建设中的技术、内容、费用、测试、维护等做出策划。网站策划对网站建设起到计划和指
- 微信小程序 环形进度条_微信小程序实现圆形进度条实例分享
易筱昭
微信小程序环形进度条
本文主要和大家分享微信小程序实现圆形进度条实例,希望能帮助到大家。小程序中使用圆形倒计时,效果图:思路使用2个canvas一个是背景圆环,一个是彩色圆环。使用setInterval让彩色圆环逐步绘制。解决方案第一步先写结构一个盒子包裹2个canvas以及文字盒子;盒子使用相对定位作为父级,flex布局,设置居中;一个canvas,使用绝对定位作为背景,canvas-id="canvasProgre
- 首次拿到无线USB转换器TOS-WLink使用介绍
TOS-WLink的开发到今持续了大半年、先不知羞耻的夸夸自己的毅力;这里主要介绍一些无线助手的使用,可能也能体现一点点我的设计思想;感谢对我帮助极大这些开源库的大佬们;感谢CSDN一些我记不住名字的作者写的文章、对USB标准的理解、C#的一些实例;无线USB助手参考:Win蓝牙GitHub-miuser00/BLEComm:BLECommbasedonnewAPIofWindows10OS.Th
- 基于灰色马尔科夫模型预测人口数量,是一种结合灰色系统理论(处理少数据、不确定性)与马尔科夫链(描述随机波动)的融合预测方法
利用灰色模型捕捉人口变化的总体趋势,再通过马尔科夫链修正因随机因素导致的预测偏差,从而提高预测精度。一、模型理论基础灰色系统理论原理(核心:处理少数据、部分信息未知的系统)差异信息原理:系统内外的差异是信息源,人口数据的时间序列差异蕴含变化规律。解的非唯一性原理:信息不完全时,预测结果存在多个可能区间(与马尔科夫状态划分契合)。最小信息原理:仅需少量历史数据(通常≥4个)即可建模,适合人口统计资料
- 深入剖析Nginx架构及其不同使用场景下的配置
LiRuiJie
NginxNginx系统架构反向代理
一、Nginx整体架构概览1.Nginx简介Nginx是采用C语言编写的高性能Web服务器、反向代理服务器及邮件代理服务器,特点是:高并发、高可用、低内存占用、模块化设计。架构核心理念:Master-Worker多进程模型事件驱动(Event-Driven)+异步非阻塞高度模块化设计2.进程模型Nginx的进程模型非常轻量,通常包含:1.Master进程启动时由shell进程fork出来主要负责:
- 【策划所需编程知识】
叫我六胖子
笔记游戏
1、TCP与UDP名称TCPUDP方式先奏后斩先斩后奏优点防外挂,慢但不出错用户体验好常用游戏MMORPGFPS、MOBA、IO类2、弱联网与实时联网名称弱联网实时联网方式只在必要时链接频率很高特点频率低频率高特点对宽带要求不高对宽带要求高常用游戏卡牌、放置挂机、轻度休闲、SLGFPS、MOBA、IO类
- 运行两个不同项目(`ragflow` 和 `dify`)时,出现了 Redis 容器互相替换
z日火
人工智能类项目redis数据库docker
问题描述在同时运行两个不同项目(ragflow和dify)时,出现了Redis容器互相替换的问题。具体表现为,当启动一个项目的Redis容器时,另一个项目的Redis容器会被停止或替换,导致两个项目的Redis容器无法同时存在。问题经过最初发现:在运行dify项目时,发现ragflow项目的Redis容器被替换为dify项目的Redis容器。尝试解决:通过修改docker-compose.yml文
- 【Python深度学习】零基础掌握Pytorch Pooling layers nn.MaxPool方法
Mr数据杨
Python深度学习python深度学习pytorch
在深度学习的世界中,MaxPooling是一种关键的操作,用于降低数据的维度并保留重要特征。这就像是从一堆照片中挑选出最能代表某个场景的那张。PyTorch提供了多种MaxPooling层,包括nn.MaxPool1d、nn.MaxPool2d和nn.MaxPool3d,它们分别适用于不同维度的数据处理。如果处理的是声音信号(一维数据),就会用到nn.MaxPool1d。而处理图像(二维数据)时,
- 误差的回响:反向传播算法与神经网络的惊天逆转
田园Coder
人工智能科普人工智能科普
当专家系统在20世纪80年代初期大放异彩,成为人工智能实用化的耀眼明星时,另一股曾经被宣判“死刑”的力量——连接主义(神经网络)——正在寒冬的冻土下悄然涌动,孕育着一场惊天动地的复苏。马文·明斯基和西摩·帕尔特在1969年《感知机》专著中那精准而冷酷的理论批判,如同沉重的封印,将多层神经网络的研究禁锢了近二十年。他们指出的核心死结——缺乏有效算法来训练具有隐藏层的网络——仿佛一道无法逾越的天堑。单
- 戴尔笔记本win8系统改装win7系统
sophia天雪
win7戴尔改装系统win8
戴尔win8 系统改装win7 系统详述
第一步:使用U盘制作虚拟光驱:
1)下载安装UltraISO:注册码可以在网上搜索。
2)启动UltraISO,点击“文件”—》“打开”按钮,打开已经准备好的ISO镜像文
- BeanUtils.copyProperties使用笔记
bylijinnan
java
BeanUtils.copyProperties VS PropertyUtils.copyProperties
两者最大的区别是:
BeanUtils.copyProperties会进行类型转换,而PropertyUtils.copyProperties不会。
既然进行了类型转换,那BeanUtils.copyProperties的速度比不上PropertyUtils.copyProp
- MyEclipse中文乱码问题
0624chenhong
MyEclipse
一、设置新建常见文件的默认编码格式,也就是文件保存的格式。
在不对MyEclipse进行设置的时候,默认保存文件的编码,一般跟简体中文操作系统(如windows2000,windowsXP)的编码一致,即GBK。
在简体中文系统下,ANSI 编码代表 GBK编码;在日文操作系统下,ANSI 编码代表 JIS 编码。
Window-->Preferences-->General -
- 发送邮件
不懂事的小屁孩
send email
import org.apache.commons.mail.EmailAttachment;
import org.apache.commons.mail.EmailException;
import org.apache.commons.mail.HtmlEmail;
import org.apache.commons.mail.MultiPartEmail;
- 动画合集
换个号韩国红果果
htmlcss
动画 指一种样式变为另一种样式 keyframes应当始终定义0 100 过程
1 transition 制作鼠标滑过图片时的放大效果
css
.wrap{
width: 340px;height: 340px;
position: absolute;
top: 30%;
left: 20%;
overflow: hidden;
bor
- 网络最常见的攻击方式竟然是SQL注入
蓝儿唯美
sql注入
NTT研究表明,尽管SQL注入(SQLi)型攻击记录详尽且为人熟知,但目前网络应用程序仍然是SQLi攻击的重灾区。
信息安全和风险管理公司NTTCom Security发布的《2015全球智能威胁风险报告》表明,目前黑客攻击网络应用程序方式中最流行的,要数SQLi攻击。报告对去年发生的60亿攻击 行为进行分析,指出SQLi攻击是最常见的网络应用程序攻击方式。全球网络应用程序攻击中,SQLi攻击占
- java笔记2
a-john
java
类的封装:
1,java中,对象就是一个封装体。封装是把对象的属性和服务结合成一个独立的的单位。并尽可能隐藏对象的内部细节(尤其是私有数据)
2,目的:使对象以外的部分不能随意存取对象的内部数据(如属性),从而使软件错误能够局部化,减少差错和排错的难度。
3,简单来说,“隐藏属性、方法或实现细节的过程”称为——封装。
4,封装的特性:
4.1设置
- [Andengine]Error:can't creat bitmap form path “gfx/xxx.xxx”
aijuans
学习Android遇到的错误
最开始遇到这个错误是很早以前了,以前也没注意,只当是一个不理解的bug,因为所有的texture,textureregion都没有问题,但是就是提示错误。
昨天和美工要图片,本来是要背景透明的png格式,可是她却给了我一个jpg的。说明了之后她说没法改,因为没有png这个保存选项。
我就看了一下,和她要了psd的文件,还好我有一点
- 自己写的一个繁体到简体的转换程序
asialee
java转换繁体filter简体
今天调研一个任务,基于java的filter实现繁体到简体的转换,于是写了一个demo,给各位博友奉上,欢迎批评指正。
实现的思路是重载request的调取参数的几个方法,然后做下转换。
- android意图和意图监听器技术
百合不是茶
android显示意图隐式意图意图监听器
Intent是在activity之间传递数据;Intent的传递分为显示传递和隐式传递
显式意图:调用Intent.setComponent() 或 Intent.setClassName() 或 Intent.setClass()方法明确指定了组件名的Intent为显式意图,显式意图明确指定了Intent应该传递给哪个组件。
隐式意图;不指明调用的名称,根据设
- spring3中新增的@value注解
bijian1013
javaspring@Value
在spring 3.0中,可以通过使用@value,对一些如xxx.properties文件中的文件,进行键值对的注入,例子如下:
1.首先在applicationContext.xml中加入:
<beans xmlns="http://www.springframework.
- Jboss启用CXF日志
sunjing
logjbossCXF
1. 在standalone.xml配置文件中添加system-properties:
<system-properties> <property name="org.apache.cxf.logging.enabled" value=&
- 【Hadoop三】Centos7_x86_64部署Hadoop集群之编译Hadoop源代码
bit1129
centos
编译必需的软件
Firebugs3.0.0
Maven3.2.3
Ant
JDK1.7.0_67
protobuf-2.5.0
Hadoop 2.5.2源码包
Firebugs3.0.0
http://sourceforge.jp/projects/sfnet_findbug
- struts2验证框架的使用和扩展
白糖_
框架xmlbeanstruts正则表达式
struts2能够对前台提交的表单数据进行输入有效性校验,通常有两种方式:
1、在Action类中通过validatexx方法验证,这种方式很简单,在此不再赘述;
2、通过编写xx-validation.xml文件执行表单验证,当用户提交表单请求后,struts会优先执行xml文件,如果校验不通过是不会让请求访问指定action的。
本文介绍一下struts2通过xml文件进行校验的方法并说
- 记录-感悟
braveCS
感悟
再翻翻以前写的感悟,有时会发现自己很幼稚,也会让自己找回初心。
2015-1-11 1. 能在工作之余学习感兴趣的东西已经很幸福了;
2. 要改变自己,不能这样一直在原来区域,要突破安全区舒适区,才能提高自己,往好的方面发展;
3. 多反省多思考;要会用工具,而不是变成工具的奴隶;
4. 一天内集中一个定长时间段看最新资讯和偏流式博
- 编程之美-数组中最长递增子序列
bylijinnan
编程之美
import java.util.Arrays;
import java.util.Random;
public class LongestAccendingSubSequence {
/**
* 编程之美 数组中最长递增子序列
* 书上的解法容易理解
* 另一方法书上没有提到的是,可以将数组排序(由小到大)得到新的数组,
* 然后求排序后的数组与原数
- 读书笔记5
chengxuyuancsdn
重复提交struts2的token验证
1、重复提交
2、struts2的token验证
3、用response返回xml时的注意
1、重复提交
(1)应用场景
(1-1)点击提交按钮两次。
(1-2)使用浏览器后退按钮重复之前的操作,导致重复提交表单。
(1-3)刷新页面
(1-4)使用浏览器历史记录重复提交表单。
(1-5)浏览器重复的 HTTP 请求。
(2)解决方法
(2-1)禁掉提交按钮
(2-2)
- [时空与探索]全球联合进行第二次费城实验的可能性
comsci
二次世界大战前后,由爱因斯坦参加的一次在海军舰艇上进行的物理学实验 -费城实验
至今给我们大家留下很多迷团.....
关于费城实验的详细过程,大家可以在网络上搜索一下,我这里就不详细描述了
在这里,我的意思是,现在
- easy connect 之 ORA-12154: TNS: 无法解析指定的连接标识符
daizj
oracleORA-12154
用easy connect连接出现“tns无法解析指定的连接标示符”的错误,如下:
C:\Users\Administrator>sqlplus username/
[email protected]:1521/orcl
SQL*Plus: Release 10.2.0.1.0 – Production on 星期一 5月 21 18:16:20 2012
Copyright (c) 198
- 简单排序:归并排序
dieslrae
归并排序
public void mergeSort(int[] array){
int temp = array.length/2;
if(temp == 0){
return;
}
int[] a = new int[temp];
int
- C语言中字符串的\0和空格
dcj3sjt126com
c
\0 为字符串结束符,比如说:
abcd (空格)cdefg;
存入数组时,空格作为一个字符占有一个字节的空间,我们
- 解决Composer国内速度慢的办法
dcj3sjt126com
Composer
用法:
有两种方式启用本镜像服务:
1 将以下配置信息添加到 Composer 的配置文件 config.json 中(系统全局配置)。见“例1”
2 将以下配置信息添加到你的项目的 composer.json 文件中(针对单个项目配置)。见“例2”
为了避免安装包的时候都要执行两次查询,切记要添加禁用 packagist 的设置,如下 1 2 3 4 5
- 高效可伸缩的结果缓存
shuizhaosi888
高效可伸缩的结果缓存
/**
* 要执行的算法,返回结果v
*/
public interface Computable<A, V> {
public V comput(final A arg);
}
/**
* 用于缓存数据
*/
public class Memoizer<A, V> implements Computable<A,
- 三点定位的算法
haoningabc
c算法
三点定位,
已知a,b,c三个顶点的x,y坐标
和三个点都z坐标的距离,la,lb,lc
求z点的坐标
原理就是围绕a,b,c 三个点画圆,三个圆焦点的部分就是所求
但是,由于三个点的距离可能不准,不一定会有结果,
所以是三个圆环的焦点,环的宽度开始为0,没有取到则加1
运行
gcc -lm test.c
test.c代码如下
#include "stdi
- epoll使用详解
jimmee
clinux服务端编程epoll
epoll - I/O event notification facility在linux的网络编程中,很长的时间都在使用select来做事件触发。在linux新的内核中,有了一种替换它的机制,就是epoll。相比于select,epoll最大的好处在于它不会随着监听fd数目的增长而降低效率。因为在内核中的select实现中,它是采用轮询来处理的,轮询的fd数目越多,自然耗时越多。并且,在linu
- Hibernate对Enum的映射的基本使用方法
linzx0212
enumHibernate
枚举
/**
* 性别枚举
*/
public enum Gender {
MALE(0), FEMALE(1), OTHER(2);
private Gender(int i) {
this.i = i;
}
private int i;
public int getI
- 第10章 高级事件(下)
onestopweb
事件
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- 孙子兵法
roadrunners
孙子兵法
始计第一
孙子曰:
兵者,国之大事,死生之地,存亡之道,不可不察也。
故经之以五事,校之以计,而索其情:一曰道,二曰天,三曰地,四曰将,五
曰法。道者,令民于上同意,可与之死,可与之生,而不危也;天者,阴阳、寒暑
、时制也;地者,远近、险易、广狭、死生也;将者,智、信、仁、勇、严也;法
者,曲制、官道、主用也。凡此五者,将莫不闻,知之者胜,不知之者不胜。故校
之以计,而索其情,曰
- MySQL双向复制
tomcat_oracle
mysql
本文包括:
主机配置
从机配置
建立主-从复制
建立双向复制
背景
按照以下简单的步骤:
参考一下:
在机器A配置主机(192.168.1.30)
在机器B配置从机(192.168.1.29)
我们可以使用下面的步骤来实现这一点
步骤1:机器A设置主机
在主机中打开配置文件 ,
- zoj 3822 Domination(dp)
阿尔萨斯
Mina
题目链接:zoj 3822 Domination
题目大意:给定一个N∗M的棋盘,每次任选一个位置放置一枚棋子,直到每行每列上都至少有一枚棋子,问放置棋子个数的期望。
解题思路:大白书上概率那一张有一道类似的题目,但是因为时间比较久了,还是稍微想了一下。dp[i][j][k]表示i行j列上均有至少一枚棋子,并且消耗k步的概率(k≤i∗j),因为放置在i+1~n上等价与放在i+1行上,同理
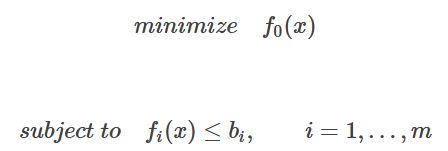
 2. 特性:
2. 特性:![]() 经过凸化,优化变量为虚拟时间τ和输入向量u,在经过线性离散化,从连续时间到离散时间,在这种情况下,虚拟时间τ被离散为N+1点。
经过凸化,优化变量为虚拟时间τ和输入向量u,在经过线性离散化,从连续时间到离散时间,在这种情况下,虚拟时间τ被离散为N+1点。