数据结构课程设计---实现一元稀疏多项式计算器

课程设计课题：
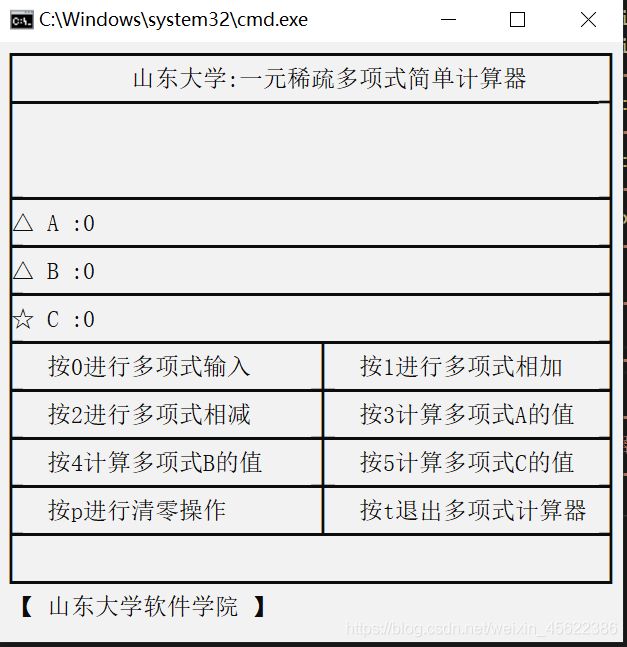
设计一个一元稀疏多项式简单计算器，能够实现五大基本功能：
（1）输入并建立多项式；
（2）输出多项式，输出形式为整数序列：n，c1，e1，c2，e2，…,cn，en，其中n是多项式的项数，ci，ei，分别是第i项的系数和指数，序列按指数降序排序；
（3）多项式a和b相加，建立多项式a+b；
（4）多项式a和b相减，建立多项式a-b；
（5）计算多项式在x处的值；

控制台输出代码

#define _CRT_SECURE_NO_WARNINGS   
#include
#include
#include
#include
typedef struct Polynomial //多项式
{
	float coef; //系数
	int expn;   //指数
	struct Polynomial *next;//指针
} Polynomial, *Polyn;
//创建一个头指针为head，项数为m的一元多项式
Polyn CreatPolyn(Polyn head, int m)
{
	head = (Polyn)malloc(sizeof(struct Polynomial));
	head->next = NULL;
	for (int i = 1; i <= m; i++)
	{
		Polyn p = (Polyn)malloc(sizeof(struct Polynomial));
		printf("请输入第%d项的系数与指数：", i);
		scanf("%f%d", &p->coef, &p->expn);
		if (p->coef == 0) free(p);
		else
		{
			Polyn q1, q2;
			q1 = head;
			q2 = head->next;
			while (q2 != NULL && p->expn < q2->expn)
			{
				q1 = q2;
				q2 = q2->next;
			}
			if (q2 != NULL && p->expn == q2->expn)
			{
				q2->coef += p->coef;
				if (q2->coef == 0)
				{
					q1->next = q2->next;
					free(q2);
				}
				free(p);
			}
			else
			{
				p->next = q2;
				q1->next = p;
			}
		}
	}
	return head;
}
void printPoLlyn(Polyn head)
{
	Polyn q = head->next;
	int flag = 0;     //记录是否为第一项
	if (!q)
	{
		puts("0");
		puts("\n");
		return;
	}
	while (q)
	{
		if (q->coef > 0 && flag == 1)
		{
			printf("+");
		}
		flag = 1;
		if (q->coef != 1 && q->coef != -1)
		{
			printf("%g", q->coef);

			if (q->expn == 1) printf("x");
			else if (q->expn!=0) printf("x^%d", q->expn);
		}
		else
		{
			if (q->coef == 1)
			{
				if (q->expn == 0) printf("1");
				else if (q->expn == 1) printf("x");
				else printf("x^%d", q->expn);
			}
			if (q->coef == -1)
			{
				if (q->expn == 0) printf("-1");
				else if (q->expn == 1) printf("-x");
				else printf("-x^%d", q->expn);
			}
		}
		q = q->next;
	}
	printf("\n");
}
int compare(Polyn a, Polyn b)//比较两个多项式的大小
{
	if (a&&b)  // 多项式a和b均不为空
	{
		if (a->expn > b->expn) return 1;// a的指数大于b的指数
		else if (a->expn < b->expn) return -1;
		else return 0;
	}
	else if (!a&&b) return -1; //a为空，b不为空
	else if (a&&!b) return 1;  //b为空，a不为空 
	else if (!a&&!b)return 0;  //a,b均为空
}
Polyn addPolyn(Polyn a, Polyn b)  //求解a+b，并返回头结点head
{
	Polyn head ,qc;
	Polyn qa = a->next;
	Polyn qb = b->next;
	Polyn hc=(Polyn)malloc(sizeof(Polynomial));
	hc->next = NULL;
	head = hc;
	while (qa || qb)
	{
		qc= (Polyn)malloc(sizeof(Polynomial));
		if (compare(qa, qb) == 1)
		{
			qc->coef = qa->coef;
			qc->expn = qa->expn;
			qa = qa->next;
		}
		else if (compare(qa, qb) == 0) //指数相同，直接相加
		{
			qc->coef = qa->coef + qb->coef;
			qc->expn = qa->expn ; 
			qa = qa->next;
			qb = qb->next;
		}
		else
		{
			qc->coef = qb->coef;
			qc->expn = qb->expn;
			qb = qb->next;
		}
         
		if (qc->coef != 0) //将该节点插入链表中
		{
			qc->next = hc->next;
			hc->next = qc;
			hc = qc;
		}
		else free(qc);		
	}
	return head;
}
Polyn subPolyn(Polyn a, Polyn b)
{
	Polyn h = b;
	Polyn p = b->next;
	while(p)
	{
		p->coef *= -1;
		p = p->next;
	}
	Polyn head = addPolyn(a, h);
	for (Polyn i = h->next; i != 0; i = i->next)
	{ 
		i->coef *= -1;
	}		
	return  head;
}
double value(Polyn head, int x) //计算x的值
{
	double sum = 0;
	for (Polyn p = head->next; p != 0; p = p->next)
	{
		int tmp = 1;
		int expn = p->expn;
		while(expn != 0) //指数不为0
		{
			if (expn < 0)   tmp /= x, expn++;
			else if(expn>0) tmp *= x, expn--;
		}
		sum += p->coef*tmp;
	}	
	return sum;
}
int main()
{
	int m;
	Polyn a = 0, b = 0;
	printf("请输入a的项数:");
	scanf("%d", &m);
	a = CreatPolyn(a, m);
	printPoLlyn(a);
	printf("请输入b的项数:");
	scanf("%d", &m);
	b = CreatPolyn(b, m);
	printPoLlyn(b);
	printf("输出 a+b：");
	printPoLlyn(addPolyn(a, b));
	printf("输出 a-b：");
	printPoLlyn(subPolyn(a, b));
	printf("请输入x的值：");
	int x;
	scanf("%d", &x);
	printf("输出a的多项式的值为：%.2lf", value(a,x));
	return 0;
}
/*
测试数据：
3
2 1
5 8
-3.1 11
3
7 0
-5 8
11 9
1
*/

控制台输出的代码没有用户界面，需要用户自己输入项数什么什么，总之是一个测试版。

具体参考课设参考

修改之后的代码具有控制台界面，代码如下：

#define _CRT_SECURE_NO_WARNINGS   
#include
#include
#include
#include
#include 
#include 
double coefs[80];  //存系数 
int expns[80];  //存指数 
int cnt, m;
double get_coef(char *str)  //在输入的字符串中提取系数
{
	double s = 0.0;
	double d = 10.0;
	bool flag = false;
	while (*str == ' ')  str++;
	if (*str == '-')//记录数字正负  
	{
		flag = true;  str++;
		if (*str == 'x') 	return -1.0;
	}
	else if ((*str == '+'&&*(str + 1) == 'x') || (*str == 'x')) return 1.0;
	if (*str == '+' && (*(str + 1) >= '0'&&*(str + 1) <= '9'))str++;
	if (!(*str >= '0'&&*str <= '9'))     return s; //如果一开始非数字则退出，返回0.0     
	while (*str >= '0'&&*str <= '9'&&*str != '.')//计算小数点前整数部分  
	{
		s = s * 10.0 + *str - '0';
		str++;
	}
	if (*str == '.')    str++;         //以后为小数部分      
	while (*str >= '0'&&*str <= '9')  //计算小数部分  
	{
		s = s + (*str - '0') / d;
		d *= 10.0;
		str++;
	}
	return s * (flag ? -1.0 : 1.0);
}
void getNums() //在输入的字符串中提取系数和指数
{
	int i = 0;
	cnt = 0;
	double coef;
	int expn;
	char str[80];
	scanf("%s", str);
	while (*(str + i))
	{
		coef = get_coef(str + i);
		if (*(str + i) != 'x') i++;
		while ((*(str + i) >= '0'&&*(str + i) <= '9') || (*(str + i) == '.'))  	i++;
		if (*(str + i) == '+' || *(str + i) == '-' || *(str + i) == '\0')            expn = 0;
		else if (*(str + i) == 'x')
		{
			i++;
			if (*(str + i) == '+' || *(str + i) == '-' || *(str + i) == '\0') expn = 1;
			else if (*(str + i) == '^')
			{
				i++;
				expn = (int)get_coef(str + i);
				while ((*(str + i) >= '0'&&*(str + i) <= '9') || (*(str + i) == '.'))i++;
			}
		}
		coefs[cnt] = coef;
		expns[cnt] = expn;
		cnt++;
	}
}
typedef struct Polynomial //多项式
{
	double coef; //系数
	int expn;   //指数
	struct Polynomial *next;//指针
} Polynomial, *Polyn;
//创建一个头指针为head，项数为m的一元多项式
void CreatPolyn(Polyn head, int m)  //建立链表，在插入过程中实现单链表有序
{
	for (int i = 0; i < m; i++)
	{
		Polyn p = (Polyn)malloc(sizeof(struct Polynomial));
		p->coef = coefs[i];
		p->expn = expns[i];
		if (p->coef == 0) free(p);
		else
		{
			Polyn q1, q2;
			q1 = head;
			q2 = head->next;
			while (q2 != NULL && p->expn < q2->expn)
			{
				q1 = q2;
				q2 = q2->next;
			}
			if (q2 != NULL && p->expn == q2->expn)
			{
				q2->coef += p->coef;
				if (q2->coef == 0)
				{
					q1->next = q2->next;
					free(q2);
				}
				free(p);
			}
			else
			{
				p->next = q2;
				q1->next = p;
			}
		}
	}
}
void printPoLlyn(Polyn head) //进行格式化打印输出
{
	Polyn q = head->next;
	int flag = 0;     //记录是否为第一项
	if (!q)
	{
		puts("0\t");
		return;
	}
	while (q)
	{
		if (q->coef > 0 && flag == 1)
		{
			printf("+");
		}
		flag = 1;
		if (q->coef != 1 && q->coef != -1)
		{
			printf("%g", q->coef);

			if (q->expn == 1) printf("x");
			else if (q->expn != 0) printf("x^%d", q->expn);
		}
		else
		{
			if (q->coef == 1)
			{
				if (q->expn == 0) printf("1");
				else if (q->expn == 1) printf("x");
				else printf("x^%d", q->expn);
			}
			if (q->coef == -1)
			{
				if (q->expn == 0) printf("-1");
				else if (q->expn == 1) printf("-x");
				else printf("-x^%d", q->expn);
			}
		}
		q = q->next;
	}
	printf("\t\t");
}
int compare(Polyn a, Polyn b)//比较两个多项式的大小
{
	if (a&&b)  // 多项式a和b均不为空
	{
		if (a->expn > b->expn) return 1;// a的指数大于b的指数
		else if (a->expn < b->expn) return -1;
		else return 0;
	}
	else if (!a&&b) return -1; //a为空，b不为空
	else if (a && !b) return 1;  //b为空，a不为空 
	else if (!a && !b)return 0;  //a,b均为空
}
void clear(Polyn c)
{
	Polyn p, q;
	p = c;
	while (p->next != NULL)
	{
		q = p->next;
		p->next = q->next;
		free(q);
	}
	c->next = NULL;
}
void addPolyn(Polyn a1, Polyn b1, Polyn c1)  //求解a+b
{
	Polyn a = a1;
	Polyn b = b1;
	Polyn c = c1;
	clear(c1);
	Polyn head, qc;
	Polyn qa = a->next;
	Polyn qb = b->next;
	head = c;
	while (qa || qb)
	{
		qc = (Polyn)malloc(sizeof(Polynomial));
		if (compare(qa, qb) == 1)
		{
			qc->coef = qa->coef;
			qc->expn = qa->expn;
			qa = qa->next;
		}
		else if (compare(qa, qb) == 0) //指数相同，直接相加
		{
			qc->coef = qa->coef + qb->coef;
			qc->expn = qa->expn;
			qa = qa->next;
			qb = qb->next;
		}
		else
		{
			qc->coef = qb->coef;
			qc->expn = qb->expn;
			qb = qb->next;
		}

		if (qc->coef != 0) //将该节点插入链表中
		{
			qc->next = c->next;
			c->next = qc;
			c = qc;
		}
	}
}
void subPolyn(Polyn a, Polyn b, Polyn c)// a-b可以用a+b来求解，把b改成-b
{
	Polyn h = b;
	Polyn p = b->next;
	while (p)
	{
		p->coef *= -1;
		p = p->next;
	}
	addPolyn(a, h, c);
	for (Polyn i = h->next; i != 0; i = i->next)
	{
		i->coef *= -1;
	}
}
void goto_xy(int x, int y)
{
	HANDLE hOut;
	hOut = GetStdHandle(STD_OUTPUT_HANDLE);
	COORD pos = { x,y };
	SetConsoleCursorPosition(hOut, pos);
}
void value(Polyn head, int flag)  //计算x的值
{
	goto_xy(2, 3); printf(" x = ");
	double sum = 0, x;
	scanf("%lf", &x);
	for (Polyn p = head->next; p != 0; p = p->next)
	{
		double tmp = 1;
		int expn = p->expn;
		while (expn != 0) //指数不为0
		{
			if (expn < 0)      tmp /= x, expn++;
			else if (expn > 0) tmp *= x, expn--;
		}
		sum += p->coef*tmp;
	}
	goto_xy(2, 4);
	if (flag == 1) printf(" A( %g )的值 = %g", x, sum);
	if (flag == 2) printf(" B( %g )的值 = %g", x, sum);
	if (flag == 3) printf(" C( %g )的值 = %g", x, sum);
}
void show(Polyn a, Polyn b, Polyn c) //界面实现
{
	goto_xy(0, 0); 	 printf("┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓\n");
	goto_xy(0, 1);   printf("┃          山东大学:一元稀疏多项式简单计算器      ┃\n");
	goto_xy(0, 2);   printf("┃━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ ┫");
	goto_xy(0, 3);   printf("┃\n"); goto_xy(50, 3);                     printf("┃\n");
	goto_xy(0, 4);   printf("┃\n"); goto_xy(50, 4);                     printf("┃\n");
	goto_xy(0, 5);   printf("┃\n"); goto_xy(50, 5);                     printf("┃\n");
	goto_xy(0, 6);   printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 7);   printf("┃△ A :"); goto_xy(7, 7); printPoLlyn(a);  goto_xy(50, 7);  printf("┃");
	goto_xy(0, 8);   printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 9);   printf("┃△ B :"); goto_xy(7, 9); printPoLlyn(b);  goto_xy(50, 9);  printf("┃");
	goto_xy(0, 10);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 11);  printf("┃☆ C :"); goto_xy(7, 11); printPoLlyn(c);  goto_xy(50, 11);  printf("┃");
	goto_xy(0, 12);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 13);  printf("┃   按7进行多项式相加     ┃   按8进行多项式相减   ┃\n");
	goto_xy(0, 14);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 15);  printf("┃   按0进行多项式输入     ┃   按enter执行确定换行 ┃\n");
	goto_xy(0, 16);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 17);  printf("┃   按1计算多项式A的值    ┃   按2计算多项式B的值  ┃\n");
	goto_xy(0, 18);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━╋━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 19);  printf("┃   按3计算多项式C的值    ┃   按t退出多项式计算器 ┃\n");
	goto_xy(0, 20);  printf("┣━━━━━━━━━━━━━━━━━━━━━━━━━┻━━━━━━━━━━━━━━━━━━━━━━━┫");
	goto_xy(0, 21);  printf("┃                                                 ┃\n");
	goto_xy(0, 22);  printf("┗━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┛");
	goto_xy(1, 23);  printf("【 一元稀疏多项式简单计算器】");
	goto_xy(2, 3);
}
void create(Polyn a1, Polyn b1)
{
	Polyn a = a1;
	Polyn b = b1;
	clear(a1);
	clear(b1);
	goto_xy(2, 3); printf("请输入多项式a :  ");   getNums();
	m = cnt;
	CreatPolyn(a, m);
	goto_xy(2, 4); printf("请输入多项式b :  ");	  getNums();
	m = cnt;
	CreatPolyn(b, m);
}
int main()
{
	Polyn a = (Polyn)malloc(sizeof(struct Polynomial)); a->next = NULL;
	Polyn b = (Polyn)malloc(sizeof(struct Polynomial)); b->next = NULL;
	Polyn c = (Polyn)malloc(sizeof(struct Polynomial)); c->next = NULL;
	system("一元多项式计算器 ");
	system("mode con cols=52 lines=25");
	// system("color e3");
	system("color 0e");
	char ch, ch1;
	while (1)
	{
		system("cls");
		show(a, b, c);
		ch = _getch();
		if (ch == '0')
		{
			create(a, b);
		}
		else if (ch == '7')
		{
			addPolyn(a, b, c);
		}
		else if (ch == '8')
		{
			subPolyn(a, b, c);
		}
		else if (ch == 't')
		{
			exit(0);
		}
		else if (ch == '1')
		{
			value(a, 1);
			ch1 = _getch();
		}
		else if (ch == '2')
		{
			value(b, 2);
			ch1 = _getch();
		}
		else if (ch == '3')
		{
			value(c, 3);
			ch1 = _getch();
		}
	}
	return 0;
}

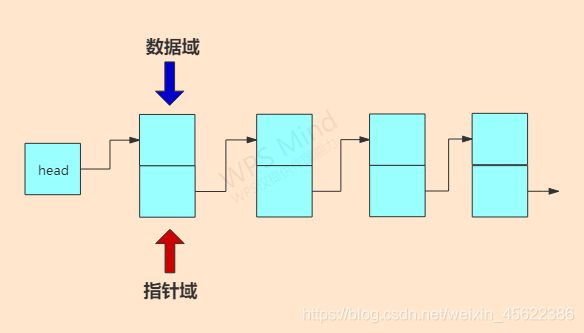
最后出来的效果图如下：

任务一 进行多项式的输入和建立

任务二进行多项式的加减

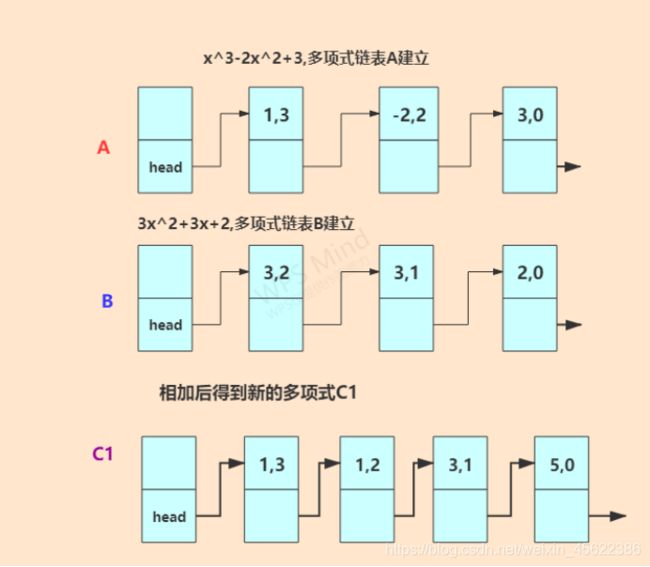
（1）多项式相加

设计思想： 我们从头到尾处理两个多项式的每一项。如果两项中，多项式a的项的指数大于多项式b的项的指数，那么将a的此项直接作为多项式c的一项。如果多项式a的指数等于多项式b的指数，将两项合并作为多项式c的一项。如果多项式a的指数小于多项式b的指数，那么将b的此项直接作为多项式c的一项。

2）多项式相减
设计思想：多项式相减的思路和多项式相加类似，A-B 就类似于 A+(-B)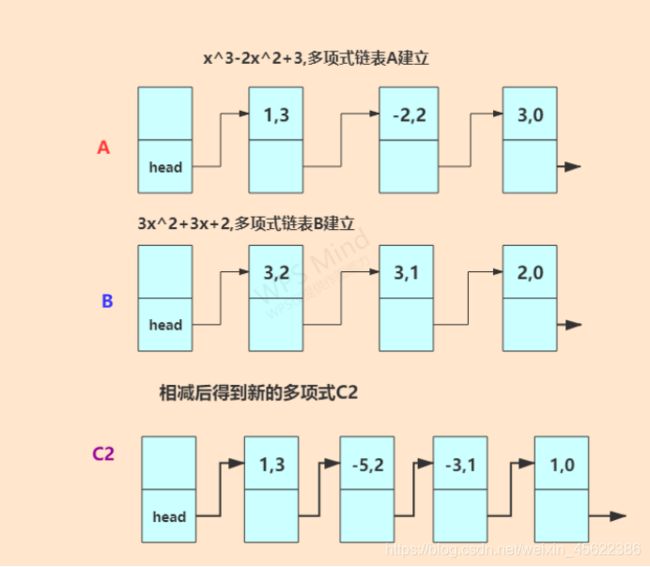
，将多项式中每个系数取反之后建立新的多项式。

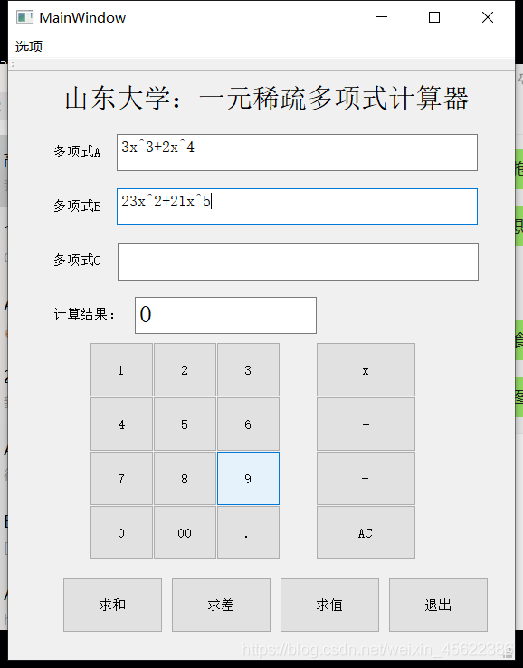
优化后的界面：

总结

现在，时隔两个星期了，我才来把总结写一下，觉得自己技术水平十分的话，只有两分。好像百废待兴，什么都需要重新来学一下，每一次课程设计，因为技术水平的不行加上自己先天的敏感体质，就会感受到情绪上的波动。

菜，确实菜，创新能力和学习能力确实比不上大佬，很多时候努努力也只是赶上平均水平。很多源码都是直接copyCSDN上很多大佬的，有的时候看不到自己的进步是件非常沮丧的事情。

这学期如果有机会我想重新找一下学习的状态，君子慎独，往往在一个人的时候越容易禁不住诱惑。做好自我管理，做事情，做好风险与收益分析。珍惜好时间和感情，提高控制时间和情绪的能力，有的时候，忍一忍，有的时候，冲一冲。人生还长，贵在细水长流。现在你就是要好好学习，提高搞钱能力，提高自己的能力是重中之重，从高中到了大学，才慢慢明白自己上大学的意义，就是有一段自己能够安静思考未来的世回见，五路你如何，能够拥有这一段奋斗岁月是一种宝贵的财富。

编程是一种积累的过程，像是写作文一样，不仅需要很坚定的基础这也是必须首先学习的，还需要有厚实基础后的创新和随心，只有让代码实现自己的想法，才能够实现编码的正反顾过程，让自己能越来越爱上编程，爱上软件开发。

当然时间是不会等你的，如果你还有着高薪梦想，你就应该尽早努力，思考未来，前路漫漫，互联网风向谁知道会在何方，还好自己已经做了考研的打算，能够给自己留有一定的上升空间，不过也要准备好工作的准备，能够在有限的时间，提高自己的能力，保持核心竞争力。

时间时间，还是时间，纵向控制好时间段，横向保证时间快为总体效率服务。