fvdm 跟驰模型 matlab仿真_MATLAB——信号灯控制下T字型路口双车道交通仿真模型...

T字型路口因为其特殊形状是交通事故多发的地段，本模型旨在建立有信号灯控制的情况下T字型路口双车道交通流模型，是用MATLAB写的元胞自动机模型。

这是仿真模型输出效果

这个模型原理其实很简单，概括的说，就是每个时间步内确定完每一个元胞的状态（包括车辆的位置信息和速度信息），然后完成位置更新。

因为没有加入车道换道功能，所以代码实现的难度其实是在T字型路口换道和直行情况的全部考虑。

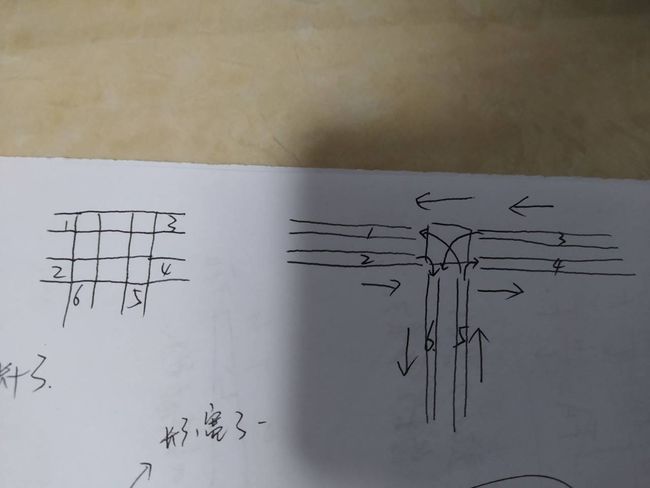
简单介绍一下T字型路口的交通情况。有信号灯控制的T字型路口的交通情况有两种状态，一个状态是横向车道允许直行，禁止左转，另一个状态是横向车道直行停止，可以左转，而右转始终可以，只要做到避让即可。

下面是对T字型路口的模型

T字型路口模型

主要思路就是将T字型路口分为两大部分，一是由六个车道组成的车道部分，二是路口（即中间方块），将六个车道的信息储存在（6，way_length/2）的矩阵中（所以横向车道是纵向车道长度的两倍，而定义横向车道长度为输入的车道长度），而将路口的信息储存在（3,3）的矩阵中。

其中，way_length是车道长度。

而车辆状态则采取元胞自动机的思想，一辆车有两个信息，位置信息和速度信息，位置信息储存在元胞矩阵中，而速度信息则受上一时间步该车辆前进方向两个元胞上有无车辆决定，但路口内车辆速度信息还有别的规则，在此不赘述。

值得注意的是：各车道非尾车（前进方向最后一辆）运行状态不受信号灯影响，2,3,5车道尾车运动状态受到红绿灯运动影响，而1,4,6车道则不受。

因此，在确定一个时间步元胞状态时，2,3,5车道尾车及路口内车辆状态就要因为信号灯而分两种状态考虑，再加上2,3,5车道尾车的换道行为，让路口内情况变得复杂，所以我写了一百多行的if语句。

整体思路就是这样，细节代码中都有，所以我先贴代码，最后再说说模型先存在哪些问题。

脚本：

%%  车流密度不变下的双向两车道仿真（T 字形路口）
%    输出参数： v_average——平均速度
%               change_lane_times——换道次数（1000 次）
%               density——车流密度
%%  参数设置 
way_length = 40;        %车道长度（偶数）
time_span = 0.1;        %仿真步长时间
MaxTime = 500;          %仿真步长数目
fp = 5;                 %车道入口处新进入车辆的概率（列向量）
pro_right_5_3=0.5;      %交叉口处车辆行为的概率向量(5 车道右转,3车道右转）
pro_right_2=0.5;        %路口处2车道右转的概率
%% 调用函数 
[ v_average, change_lane_times, density ] = CA_T_model ( way_length,time_span,fp,MaxTime,pro_right_5_3,pro_right_2);
%%  输出参数
disp('平均速度为：')
disp( v_average)
disp('换道次数为：')
disp(change_lane_times)
disp('交通流密度为')
disp(density)

函数：

%%   本函数为在某一特定车流密度下的（车流密度由 fp 决定）双向两车道仿真模型
%%   注意：
      %由红绿灯控制两个状态，一是可以横向车道直行，二是横向车道直行停止，可以左转，右转始终可以做到避让即可
      %每个车辆都有两个信息，一是位置信息（用way储存），而是速度信息（用v储存），其中速度包括慢车，快车，停车，分别用1,2,3表示
      %为了储存方便，横向车道（不包括路口方块方块）为纵向车道长度的两倍，而将横向车道长度定义为车道长度
      %此模型中信号灯只有红灯和绿灯，红灯时长可以通过参数time_red_light来调节
      %转弯路径说明：5车道左转通过（3,2），（2,1），（1，1）到达way（1,1）；右转则通过（3,3）到达way（4,1）
      %所有车辆进入路口速度最大为1
%%   参数说明：
      % 换道次数:change_lane_times
      % 平均速度;v_average
      % 平均密度;density
      % way_number:车道数目
      % way_length:车道长度
      % v_average:平均速度
      % density:车流密度
      % MaxTime:仿真步长数目
      % time_span：输出图片变换间隔时间
      % fp:车道入口处新进入车辆的概率列向量（2,3,5 车道）
      % pro_left:路口处车辆行为的概率向量(5 车道右转,3车道右转）
      % pro_right:路口处2车道右转的概率
function [ v_average, change_lane_times, density ] = CA_T_model( way_length,time_span,fp,MaxTime,pro_right_5_3,pro_right_2)
%%  初始化换道次数
change_lane_times=0;
%%  双车道
way_number=2;     
%%  设置红灯时长
time_red_light = 50;
%%  创建T字形路口
%%  构造元胞空间
space = ones(way_number+1+way_length/2 , way_length+3);  
%T字路口空间宽度由车道数+1(横向车道及分隔带所占空间)加车道长度的一半（纵向车道所占空间）
%空间长度由车道长度（横向车道所占空间）+  中间路口所占纵向3个元胞空间
%%  将元胞空间中非车道元胞赋值为1.2
space(way_number/2+1,[1:way_length/2 , way_length/2+4:way_length+3] )=1.2;          %分隔带
space(way_number+2:way_number+1+way_length/2 , [1:way_length/2 way_length/2+4:way_length+3])=1.2;   %除车道及分隔带以外空间
%%  投放初始车辆
space(1:way_number/2 , end)=0;                   %横向上车道最右边有车
space(way_number/2+2:way_number+1 , 1)=0;        %横向下车道最左边元胞有车
space(end , way_length/2+3)=0;                   %纵向车道右下角元胞有车 
%%  显示初始交通流图
figure('name','T字型路口交通模拟');
H=imshow(space,[]);              
set(gcf,'position',[241 132 560 420]) ;%241 132 560 420
set(gcf,'doublebuffer','on'); %241
title('T字型路口模拟','color','b');
%%  初始化存储元胞上车辆速度的矩阵  
v_n(1:way_number*2+2,way_length/2-2) = 0;      %v_n储存前n-2个元胞的速度
v_last(1:way_number*2+2,1:2) = 0;              %v_last储存后两个元胞的速度
v_block=zeros(way_number+1,3);                 %v_block储存方块元胞速度
%%  初始化换道频率、平均速度、车流密度相关变量
time_change_lane_times = 0;                    %time_change_lane_times用来计数一个时间步内换道次数
time_v_average(1:MaxTime) = 0;                 %time_v_average用来储存各时间步的速度
time_density(1:MaxTime) = 0;                   %time_density用来储存各时间步的交通密度
turn_left_5_end = 0;                           %标记way（5,end）处车辆的左转状态，值为1表示车辆已经确定要左转
turn_left_3_2 = 0;                             %标记（3,2）处车辆的左转状态，值为1表示车辆已经确定要左转
turn_right_3_1 = 0;                            %标记way（3,1）处车辆的右转状态，值为1表示车辆已经确定要右转
%%  时间步循环
for time = 1:MaxTime      
%%  将整个道路分为六段加路口
%%  way储存车道六部分元胞状态
way=[
space(1:way_number/2 , way_length/2:-1:1);                           %横向上车道的左边部分，方向为从右向左,1行
space(way_number/2+2:way_number+1 , 1:way_length/2);                 %横向下车道的左边部分，方向为从左到右，2行
space(1:way_number/2 , way_length+3:-1:way_length/2+4);              %横向上车道的右边部分，方向为从右向左，3行
space(way_number/2+2:way_number+1 , way_length/2+4:way_length+3);    %横向下车道的右边部分，方向为从左到右，4行
space(way_number+1+way_length/2:-1:way_number+2 , way_length/2+3)';  %纵向车道右半部分，方向为从下到上，5行
space(way_number+2:way_number+1+way_length/2 , way_length/2+1)'      %纵向车道左半部分，方向为从上到下，6行
];
%%  block储存路口元胞状态
block=space(1:way_number+1 , way_length/2+1:way_length/2+3); 
%%  确定前 n-2 个车辆的状态
     v_n(:,:) = 0;       
    %%  快速行驶的车:一个元胞本身有车而前方两个元胞状态均为无车
     v_n(way(: , 1:end-2)==0&way(: , 2:end-1)==1&way(: , 3:end)==1)=2;
    %%  停车的车：一个元胞本身有车而前方元胞也有车
     v_n(way(: , 1:end-2)==0&way(: , 2:end-1)==0)=3;    
    %%  慢速行驶的车：一个元胞本身有车而前方两个元胞状态分别为无车，有车
     v_n(way(: , 1:end-2)==0&way( : ,2:end-1)==1&way(: , 3:end)==0)=1;
%%  确定最后 2 个元胞的速度
    %%  确定倒数第 2 个元胞速度
    v_last(:,:)= 0;
    v_last(way(: , end-1)==0&way(: , end)==0) = 3;
    v_last(way(: , end-1)==0&way(: , end)==1) = 1;
%%  确定最后一个元胞及路口内元胞的状态
        %%  判断（3,1）处车辆状态
         if block(3,1)==0         
           %%  判断是否右转
            if randway_length/2)   
       time_v_average(time) = v_sum/car_number;
    end
    %%  在车道入口处随机引入新的车辆
    way([2,3,5],1)=(round(fp.*rand(3,1))&way([2;3;5],1));
    %%  特殊状态重置
    way(way~=0)=1;
    if turn_right_3_1==1
       way(6,1)=0;
       turn_right_3_1=0;
    end
    %%  将状态变化储存到元胞矩阵中
    space(1,1:way_length/2)=way(1:way_number/2,end:-1:1);
    space(3,1:way_length/2)=way(way_number/2+1:way_number,:);
    space(1,way_length/2+4:way_length+3)=way(way_number+1:way_number*3/2,end:-1:1);
    space(3,way_length/2+4:way_length+3)=way(way_number*3/2+1:2*way_number,:);
    space(way_number+2:way_number+1+way_length/2,way_length/2+3)=way(2*way_number+1,end:-1:1)';
    space(way_number+2:way_number+1+way_length/2,way_length/2+1)=way(3*way_number,:)';
    space(1:3,way_length/2+1:way_length/2+3)=block(:,:);
    %%  获得总的换道次数
    change_lane_times =  change_lane_times+time_change_lane_times;
    %%  显示交通流图
    set(H,'CData',space);
    %%  输出图片变换间隔时间
    pause(time_span);
end
    %%  获得仿真的换道次数的平均速度以及平均密度
    change_lane_times = time_change_lane_times;
    density = mean(time_density);   
    v_average = sum(time_v_average)/time;   
end

本模型还有几个需要解决的问题：

1. 速度规则是根据前方（前进方向）两个元胞的状态决定，和现实生活中驾驶员根据前车距离调整车速这一事实基本吻合，但是忽略了驾驶员对速度的追求，以及没有考虑到驾驶过程中种种意外情况导致的减速情况。

如采用NaSch模型中的速度规则

v->min(v+1,v_max)

v->min(v,d)

v->max(v-1,0) （以一定概率p）

其中，v——车辆速度

d——与前车距离

则可以克服这个问题，但是本模型加速规则因为由前方（前进方向）两个元胞状态决定，所以在位置更新时不必再考虑前方车龄情况，也就是说NaSch速度规则的引入将会程序变得复杂，尤其是在路口内，按实际情况路口内车辆速度全部取为1（车辆慢行）是合适的，就不需要另做速度规则 ，另外，车辆左右转弯，NaSch速度规则也不再适用，不过将NaSch速度规则用在车道，而路口内车辆速度规则不变倒是可以，只是储存起来比较麻烦。

2.新车辆投放方法不太好控制，现有方法是设置概率矩阵，每个时间步结束后，依据产生的随 机数和概率矩阵运算的结果向1,4,6车道投放新的车辆。这需要一个合适的矩阵算法，以及相应的输入变量规则或是大致范围对应的投放速度，这需要比较好的数学能力。

3.原本想做一个车道数可以变换的模型，但是后来发现车道变化对路口车辆运行情况影响比较大，又需要多写很多if语句，索性就按两车道的模型写了下去，但代码中任然有way_number，只是不需要输入，默认为2。

4.本模型现与现实最不符合的地方就在于没有实现车道上的换道行为。不过本模型本就重在T字型路口的仿真，所以基本任务量都在路口情况的实现。

这段时间准备写一个含有换道行为的交通流模型。

最后还是希望看到这个程序的大佬可以给出建议，有想一起学习的小伙伴可以加我哈。