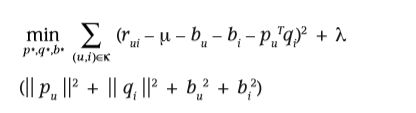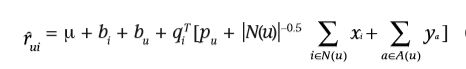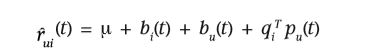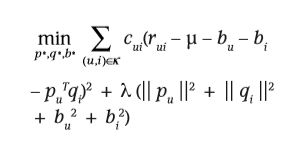MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS论文笔记;推荐系统中的矩阵分解(MF)
MATRIX FACTORIZATION TECHNIQUES FOR RECOMMENDER SYSTEMS
Yehuda Koren, Yahoo Research
Robert Bell and Chris Volinsky, AT&T Labs—Research
在看到MF的时候不太清楚,这个具体是个啥,说是根据SVD进行矩阵的分解,在看了论文后有了一个大体的了解。现在先大概的介绍下思路:假设用户物品的评分矩阵A是m*n维,即一共有m个用户,n个物品.通过算法转化为两个矩阵P和Q,矩阵P的维度是m乘k,矩阵Q的维度是n乘k。其中 P u j P_{uj} Puj表示用户u对第j个因素的偏好程度, Q i j Q_{ij} Qij表示item i在第j个因素上的程度。
在文章开头提到在商品推荐种矩阵分解要优于最近邻技术,可以合并其他信息,例如隐式反馈,时间效应和置信度。
电子零售商和内容提供者为了提高消费者对其的满意度和忠诚度,对于推荐系统有了较大的兴趣,可以分析用户的对于产品的兴趣,给出个性化的推荐
- **Recommender System Strategies **
介绍之前的推荐算法。
content filtering:有对用户和商品进行画像的描述从而进行推荐;或者只基于用户的过往行为:交易行为,产品打分等。
collaborative filtering:相比于内容过滤,协同过滤更为准确,可以无视领域问题,对于难以刻画形象的物品或用户可以很好的处理;不过其却会面临冷启动的问题,在这个问题上,内容过滤要表现的好一点。
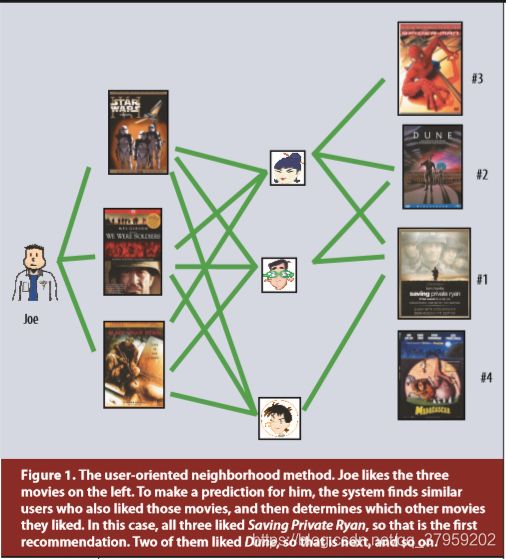
其中协同过滤还可以分为两类:邻域方法和潜在因子模型(neighborhood methods and latent factor models)
其中neighborhood method又可以分为item-oriented approach和user-oriented approach两种,分别计算item或user之间的关系。
latent factor models尝试解释评分,通过将item和user特征化表示。
举例在两个维度上:serious-escapist,male-female。其中用户Dave和电影Ocean’s 11在这两个维度上就比较中立。某个用户可能就会喜欢看Dumb and Dumber,而不喜欢The Color Purple,Braveheart的评价可能就会比较中立。评分相当于用户和电影在图中位置的点积。
-
Matrix Factorization Methods
latent factor 最成功的实现是基于矩阵分解的(Some of the most successful realizations of latent factor models are based on matrix factorization. )
关于推荐系统的输入数据,通常是输入一个矩阵,其中矩阵的一个维度用来表示用户,其他维度表示用户感兴趣的item。这其中最便利的数据就是显示反馈(explicit feedback),类似于用户对于item的评分或者打星又或者类似于B站的赞和不赞等;当用户的显示反馈不易得到时,可以使用用户的隐式反馈(implicit feedback),类似于用户的购买记录,搜索模式或者鼠标的移动等信息。
关于矩阵分解的优势就在于可以合并附加的信息进行推荐,如果显示反馈不易得到,可以使用隐式反馈的信息。
其中关于显示反馈,得到的矩阵通常稀疏的,因为item是很多的,而单个用户感兴趣的item通常只有一小部分(Usually, explicit feedback comprises a sparse matrix, since any single user is likely to have rated only a small percentage of possible items)。关于隐式反馈,通常一个事件都是发生或者没发生,所以通常得到的是一个比较密集的矩阵(Implicit feedback usually denotes the presence or absence of an event, so it is typically represented by a densely filled matrix. )。
-
**A Basic Matrix Factorization Model **
通过将user 和item使用latent factor将其映射到维度为f的空间。
每个item i 被表示为 q i ∈ R f q_i\in R^f qi∈Rf,每个user u 被表示为 p u ∈ R f p_u\in R^f pu∈Rf.他们的点积被当作用户对item打分的一个近似,被表示为 r − u i = q i T p u \overset{-}r_{ui}=q_i^Tp_u r−ui=qiTpu
主要的挑战就是如何得到映射关系,从而得到 q i , p u q_i,p_u qi,pu
文章中提到可以使用奇异值分解(SVD),但是矩阵很稀疏,所以会比较麻烦,而且数据较少,也同意引起过拟合问题。之前的系统使用的方法是通过估算来使得矩阵边密集,但这样的估算可能并不准确,可能会歪曲数据,误导模型的学习;因此,最近的方法都是只使用观察到的数据,并且使用正则化项避免过拟合。
-
**Learning Algorithms **
两种方法求解上边方程的最小化,分别是随机梯度下降和交替最小二乘。下边是详细的解释。
- stochastic gradient descent
- alternating least squares
- stochastic gradient descent
对于每个给定的训练例子,计算相关误差:
e u i = d e f r u i − q i T p u e_{ui} \overset{def}= r_{ui}-q_i^Tp_u eui=defrui−qiTpu
按照与梯度相反的方向进行参数的更新
这个方法易于实现,而且相对快速。
- alternating least squares****
固定q,p中的一个,去优化另一个,交替固定,最终会收敛.
关于ALS的优点:1.可以并行化,每个item factor之间是相互独立的,每个user factor之间也是相互独立的。突然关于这个item factor 和之前的product这些的定义有点迷??????究竟每个具体是指代啥????以及为啥是相互独立的?????我以为是相当于顺序执行来着
2.可以处理稀疏的训练集的情况
-
Adding Biases
在打分过程中,存在部分用户较为严格,在同一个作品中会相比于其他人打分较低,但只从该用户的历史来看,他对其评价和其他人对这部电影的评价相同。由此引入偏置的定义,处理这种情况的发生。
偏置定义为: b u i = μ + b i + b u b_{ui}=\mu +b_i +b_u bui=μ+bi+bu
其中 μ \mu μ为所有item的平均评分, b i b_i bi表示某个特定item i 的平均评分, b u b_u bu表示某个特定用户 u 的平均评分。
For example, suppose that you want a first-order estimate for user Joe’s rating of the movie Titanic. Now, say that the average rating over all movies, µ, is 3.7 stars. Furthermore, Titanic is better than an average movie, so it tends to be rated 0.5 stars above the average. On the other hand, Joe is a critical user, who tends to rate 0.3 stars lower than the average. Thus, the estimate for Titanic’s rating by Joe would be 3.9 stars (3.7 + 0.5 - 0.3).
所以将其带入方程可得 r − u i = μ + b i + b u + q i T p u \overset{-}r_{ui}=\mu +b_i +b_u+q_i^Tp_u r−ui=μ+bi+bu+qiTpu
最小化误差函数相应的变为如下形式:
关于偏置的设定,还有更多的论文讨论了多种多样的偏置形式
- **additional input sources **
存在冷启动问题,为了解决这个问题,采用用户的额外信息进行解决,例如采用隐式反馈,如用户的购买历史等,得到用户的偏好;或者采用已知的用户信息,例如年龄,收入层级,邮编等。
将上边提到的两种信息加入用户可得:
上边是增强用户的表示能力,必要时可以对item进行类似的操作。
- **TemporaL Dynamics **
文章中提到上边的模型是静态的,而在现实中,随着选择增多,产品的认知度和受欢迎程度是随时间变化的,是动态的。用户随着时间的发展,其爱好可能会发生改变,他可能最初喜欢龙珠,过了几年可能又会喜欢火影忍者等,所以用户的偏好是随着时间进行变化的;用户的评分可能也会随着其身份的改变或时间的变化发生改变,可能用一部电影,最初会给一个平均分4,但后来用户的平均分可能就会变为3,所以用户的评分也是随着时间而变化;item的评分也会随着时间的变化而变化,可能一部电影或一首歌会因为某些事件的发生而重新流行或不再流行,其评分也会发生变化,就像近期的last dance重新流行;而item的表示因为是一个静态的实体,所以不会随时间变化。对应的,相关的方程可以有如下形式:
- **Inputs With Varying Confidence Levels **
文章中提到不是所有的评分都值得相同的权重,原因在于可能存在部分广告用户(adversarial users)尝试倾斜某些item的评分。我个人的理解可能就相当于刷好评吗??强行把分刷上去。
还有一个问题就是基于隐式反馈的系统,可能没有办法得到一个关于用户偏好的明确的量化。
为了解决这些问题,引入置信分数(confidence score)的概念,描述用户看某个特定item的频率( Confidence can stem from available numerical values that describe the frequency of actions, for example, how much time the user watched a certain show or how frequently a user bought a certain item)
将置信分数 c u i c_{ui} cui引入方程得到如下形式:
参考链接
推荐系统中的矩阵分解