数字图像处理第三章-----灰度变换

目录

一：灰度变换与空间滤波

二.灰度变换

2.1 图像反转

 2.2 对数变换

2.3 幂律变换（伽马变换）

---

一：灰度变换与空间滤波

图像处理中分为空间域的变换和频率域的变换，

空间域：

      指的时图像的平面本身，这类方法是对图像中的像素直接操作。其在计算上相比于频率域变换更有效，且执行所需的处理资源较少。

频率域：

        图像频率域的理解

空间域处理可由下式定义：

其中，时输入图像，是处理后的图像，是在点领域上定义的关于的一种操作（算子）。邻域通常是中心在的矩形，有时也采用其他形状，如圆的数字近似，但矩形邻域是到目前为止最好的邻域，因为它在计算机上实现起来更容易。 当领域的大小不是1*1时，利用滑动的窗口在图像空间中做空间域的操作，当前的像素点由周围像素点决定，这种操作的过程叫做空间滤波。但是最小领域的大小为1*1，在这种情况下，仅仅取决于点处的值，这个时候空间域的处理公式变为（灰度级变换函数或者映射函数）：

其中和为所定义的变量，分别是和在任意点的灰度值
空间域的处理分为：灰度变换和空间滤波

二.灰度变换

2.1 图像反转

        图像反转可以得到灰度级范围为【0，L-1】的图像的反转图像，该反转图像由下式给出：

        其中是反转后图像的像素值，是反转图像的灰度级。使用这种方式反转一幅图像的灰度级，可以等效的得到照片的底片。适用于增强嵌入图像暗色区域的白色或灰色细节，特别是当黑色面积在尺寸上占主导地位时。

 PYthon代码实现：

from PIL import Image
import numpy as np

def img_inversion(img_path):
    image = Image.open(img_path)
    image.show()
    img = np.array(image)
    imgs = 256-img-1
    img=Image.fromarray(np.uint8(imgs))
    img.show()

if __name__ == '__main__':
    img_path=r'1.jpg'
    img_inversion(img_path=img_path)

 实现后的效果如下：

上图左边为原图，右边为图像反转后的图像，可以看出反转后黑色区域变亮了，亮的区域变暗了。

 2.2 对数变换

        对数变换主要用于将图像的低灰度值部分扩展，将其高灰度值部分压缩，以达到强调图像低灰度部分的目的。变换方法由下式给出:

 其中为常数，并且假设，加1可以使函数向左移一个单位，得到的均大于0。注意：因为的取值范围常为0~255，所以的取值范围为也是0~255，那么的取值范围为0~2.40824，如果的取值非常小，那么对数变换后图像的像素值的取值范围为：0~2.40824c，也是非常小的，这样会产生一张全黑的图，人眼不能分辨。可以看出相当于一个缩放的尺度。

        由上图可以看到采用对数变换时，对于输入图像，灰度值在[0,L/4]（其中L是图像的灰度级）范围类变换到[0,3L/4],可以看出图像低灰度值的部分进行了扩展，而高灰度值的部分被压缩了。即（灰度值范围一般从0到255,白色为255,黑色为0）当灰度值在0~64范围会被扩展，也就是当c取得比较大的时候，黑色区域会变小，一部分像素值接近于64区域会变亮。反对数函数的作用于此相反，反对数变换是把图像低灰度值的部分进行压缩，高灰度值的部分进行扩展。

python实现：

def img_log_transformation(img_path):
    img = Image.open(img_path)
    
    # 此处把PIL图像转换为numpy，这样方便做对数变换
    img = np.array(img)
    c=45
    img = c * np.log(1.0 + img)

    img = Image.fromarray(np.uint8(img))
    img.save('6.png')

if __name__ == '__main__':
    img_path=r'1.jpg'
    # img_inversion(img_path=img_path)
    img_log_transformation(img_path)

 实现后的效果：

上图左边为原图，右边为对数变换后的图像，，从右边可以看到，在接近岸边和船旁边的原本黑色区域变亮了，这是因为图像低灰度值的部分进行了扩展，被映射到高范围的区域了。但是船本身的细节也模糊了，这是因为船本身的像素值是比较高的，通过对数变换之后，像素值被压缩了。

注意：对数变换将源图像中范围较窄的低灰度值映射到范围较宽的灰度区间，同时将范围较宽的高灰度值区间映射为较窄的灰度区间，从而扩展了暗像素的值，压缩了高灰度的值，能够对图像中低灰度细节进行增强。

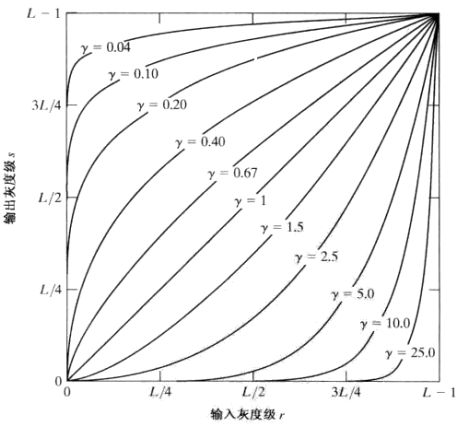
2.3 幂律变换（伽马变换）

 幂次变换的基本形式为：

其中和为常数，当时，就是恒等变换，恒等变换就是输入像素值等于输出像素值。

 由上图可以看出，当时，低灰度区域被压缩，高灰度区域被扩展， 处理漂白的图片，进行灰度级压缩。当时， 低灰度区域被扩展，高灰度区域被压缩，（灰度值范围一般从0到255,白色为255,黑色为0）处理过黑的图片，对比度增强，使得细节看的更加清楚。

注意八位的像素值最大为255，当像素值过大，产生的像素值可能超过范围，故可能发生溢出，产生截断，这个时候c的取值起到了一个调控作用。

python实现：

def img_gamma_transform(img_path):
    img = Image.open(img_path)

    # 此处把PIL图像转换为numpy，这样方便做对数变换
    img = np.array(img)
    c = 45
    img = c * np.power(img,2)

    img = Image.fromarray(np.uint8(img))
    img.save('gamma_transform.png')

if __name__ == '__main__':
    img_path=r'4.jpg'
    # img_inversion(img_path=img_path)
    # img_log_transformation(img_path)
    img_gamma_transform(img_path)

 可视化的效果：

当，时。

原图

        从上图可以看出，时，像素值比较大的时候，如果的取值比较大，那么经过变换后，像素值会超过255，细节就不存在了。

当，c=1时

原图

         从上图可以看出，，像素值最大值为255，越小，像素值经过变换后越小，图像越模糊。