最大流网络之Push-Relabel算法
上一篇文章介绍了网络最大流中的Ford-Forkerson算法和它的改进版本。对于解决网络最大流、最小割相关问题,今天我们来看一个效率更快的算法Push-Relabel算法。
1.Push-Relabel算法思想
对于一个网络流图: 该算法直观可以这样理解,先在源节点处加入充足的流(跟源节点 s 相连的所有边的容量之和),然后开始按一定规则进行流渗透,一个边一个边的向汇点渗透,直到没法再渗透(类似于Ford-Fulkerson算法中找不到增广路径了),那么这时再把一些剩余的流回收到源节点s就可。
主要分为两个步骤:push和relabel。push表示从所有节点找出一个存水量大于0的节点 u ,将它所存的水尽可能推向与它相邻的节点v。要实现该push的操作必须满足下面条件:该点存水量 e(u)>0 ,节点 u 的高度大于节v的高度。本次推送的流值 (u,v).f=mine(u),(u,v).capacity , (u,v).capacity 为边 edge(u,v) 的当前容量,这个值在推进过程中会一直变换。relabel表示某一个节点存水量大于0但水流不出去时,我们对该节点高度增加1,这就是所谓relabel操作,使得该节点的存水量流入比它低的节点。一开始的时候我们设置源节点高度为 N,此处N为节点数 ,其他所有节点高度为0,并且汇节点的高度固定为0,其他节点高度在算法执行过程中高度 h 会改变。
算法步骤:
1.初始化前置流:将与源点s相连的管道流量f(0,i)设为该管道的容量,即 f(0,i)=c(0,i);将源点s的高度h(0)=V,(V表示图的顶点个数),其余顶点高度h(i)=0;将源的点余量e(0)设为源容量减去源的流出量,即e(0)=-∑f(0,i)=-∑c(0,i),与源s相连的点余量设为该点的流入量e(i)=c(0,i),其余点都为0。
2.搜索是否有节点的点余量e(u)>0,如果存在,表示要对该点进行操作——重标记或者压入流:检查与该点u全部的相邻点v,若该点比它相邻点的高度大h(u)>h(v),该管道的当前容量为 c(u,v) ,将该点u的余量以最大方式压入该管道 delta=min(e(u),c(u,v)) , 然后对节点u,v的余量e、边(u,v)的容量进行相应的进行减加操作;如果找不到高度比自己低的相邻节点v,则对节点u的高度增加1,即 h(u)=h(u)+1 。如此继续进行Push操作。以上的重标记或压入流操作循环进行,直至该点的余量e(u)为0。
3.重复第2步,直找不到余量大于0的节点,停止算法,最后输出汇点t的余量e(t), 该值就是最后所求的最大流。最小割。
2.Push-Relabel算法原理示意图
给定的网络流图如下:

第一步:初始化操作:

第一次Push不成功,进行Relabel
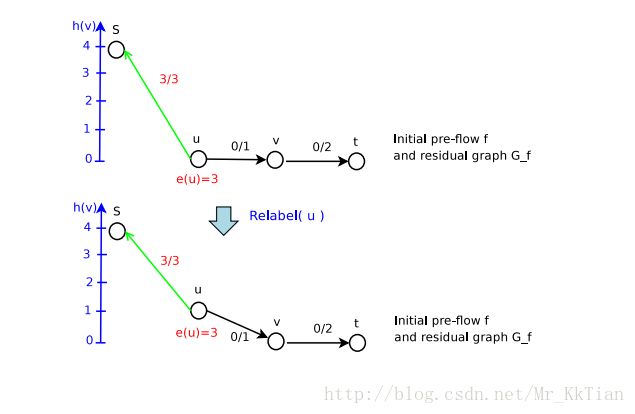
第二次Push,成功

继续Push

继续Push
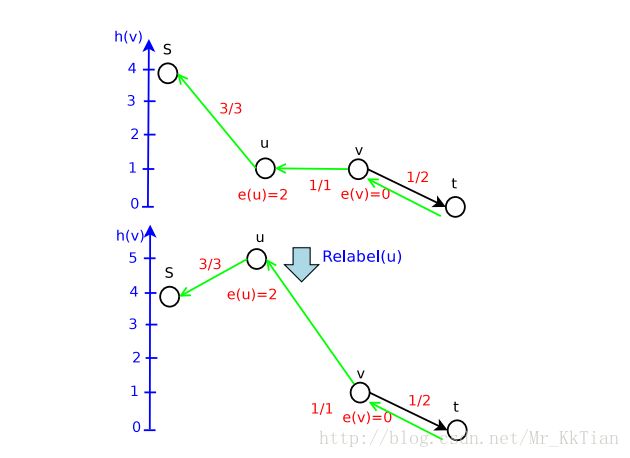
继续Push

至此结束。
3.Push-Relabel算法具体实例
求解下面网络流图的最大流:

源节点为 s ,汇节点为t
具体程序实现如下:
/****************************************************
Description:Push-Relabel算法求解网络最大流
Author:Robert.TY
Date:2016.12.10
****************************************************/
#include
using namespace std;
struct Point{
char ch;//节点标识
int e;//存货量
int h;//高度
};
Point point[6];
int graph[6][6]={{0,10,10,0,0,0},
{0,0,2,8,4,0},
{0,0,0,9,0,0},
{0,0,0,0,9,10},
{0,0,0,0,0,10},
{0,0,0,0,0,0}} ;
int Push_Relabel(int s, int t,int n); //参数为 起点 端点 节点数
int main(){
int n=6;
point[0].ch='s'; point[0].e=0; point[0].h=0;
point[1].ch='u'; point[1].e=0; point[1].h=0;
point[2].ch='v'; point[2].e=0; point[2].h=0;
point[3].ch='a'; point[3].e=0; point[3].h=0;
point[4].ch='b'; point[4].e=0; point[4].h=0;
point[5].ch='t'; point[5].e=0; point[5].h=0;
cout<<"原始网络图邻接矩阵:"<for(int i=0;i<=5;i++){
for(int j=0;j<=5;j++){
cout<6)<" ";
}cout<cout<<"max_flow="<0, n-1,n)<cout<<"graph流图矩阵:"<for(int i=0;i<=5;i++){
for(int j=0;j<=5;j++){
cout<6)<" ";
}cout<return 0;
}
int Push_Relabel(int s, int t,int n)
{
int max_flow;
point[s].h = n; //起始点高度置为n 最高
//初始化 将start点的库存 流出去 update剩余图
for (int u = 1; u <= t; u++) {
if (graph[s][u] > 0) {
point[u].e = graph[s][u];
point[s].e -= graph[s][u];
graph[u][s] = graph[s][u];
graph[s][u] = 0;
}
}
while(1) {
int finishflag = 1;
for (int u = s+1; u < t; u++) { //搜索除 节点s 节点t以外的节点
if (point[u].e > 0) { //发现库存量大于0的节点 u 进行push
finishflag = 0;
int relabel = 1; //先假设顶点u需要relabel 提高高度h
for (int v = s; v <= t && point[u].e > 0; v++) { //搜索能push的顶点
if (graph[u][v] > 0 && point[u].h >point[v].h) { //发现节点v
relabel = 0; //顶点u不需要relabel
int bottleneck = min(graph[u][v], point[u].e);
point[u].e -= bottleneck; //u节点库存量减少
point[v].e += bottleneck; //v节点库存量减少
graph[u][v] -= bottleneck;
graph[v][u] += bottleneck;
}
}
if (relabel==1) { //没有可以push的顶点,u节点需要relabel 提高高度
point[u].h += 1;
}
}
}
if (finishflag==1) { // 除源点和汇点外,每个顶点的e[i]都为0
max_flow = 0;
for (int u = s; u <= t; u++) {
if (graph[t][u] > 0) {
max_flow += graph[t][u];
}
}
//cout<<"max_flow="<
break;
}
}
return max_flow;
}
