赫夫曼树及赫夫曼编码、译码的算法实现
赫夫曼树及赫夫曼编码是数据结构与算法中的一个重要知识点,在生活中也是应用广泛,现在我来教大家如何构建一颗赫夫曼树并且实现它的赫夫曼编码。先讲解思路,后面会附完整代码及运行效果图。
构建赫夫曼树的算法思路如下
1.输入一串字符,统计出每个字符的出现频度创建字符频度表。
typedef struct //字符频度表
{
int weight; //权值
char c; //对应字符
}F_W;
F_W w[100];//字符频度存放数组
int char_count(string s,char a) //计算单个字符频度
{ int i,count=0;
for(i=0;i<s.length();i++)
if(s[i]==a) //如果字符a出现一次 count+1
count++;
return count;
}
void create_w(string s) //创建字符频度表w
{ int i,j,flag;
w[0].weight=char_count(s,s[0]);//先统计第一个字符频度并入表
w[0].c=s[0];
int t=1; //t表示数组的循环变量
for(i=1;i<s.length();i++)
{ flag=1; //表示这个字符之前没有出现过
for(j=0;j<i;j++)
{if(s[j]==s[i])//如果这个字符之前已经出现过
{ flag=0;
break;
}
}
if(flag==1) //如果之前没出现过,统计该字符频度并放进数组w
{ w[t].weight=char_count(s,s[i]);
w[t].c=s[i];
t++;
}
}
}
2.从频度表中选择权值(即频度)最小的两个节点依次构建赫夫曼树
typedef struct
{ int weight; //权值
int parent,lchild,rchild;//双亲及左右孩子
char c; //对应字符
}HTNode,*HuffmanTree;
void Select(HuffmanTree HT,int j,int &s1,int &s2) //在所有的字符节点中挑选两个权值最小的赋值给s1,s2
{ int i,k,min1=0,min2=0;
for(i=1;i<=j;i++)
{ if(HT[i].parent!=0) //如果节点已经有双亲则不算在比较范围内
continue;
if(HT[min1].weight>HT[i].weight)
min1=i;
}
for(k=1;k<=j;k++)
{ if(HT[k].parent!=0) //如果节点已经有双亲则不算在比较范围内
continue;
if(k==min1) //如果循环到min1直接跳到下一个,不能让min1的值与min2的值相等
continue;
if(HT[min2].weight>HT[k].weight)
{
min2=k;
}
}
s1=min1;
s2=min2;
}
int Init(HuffmanTree &HT,F_W *w,int n) //初始化赫夫曼树
{ if(n<=1)
return 0;
int m=2*n-1,i; //m表示总结点数
int s1,s2; //存储最小两节点的变量
HuffmanTree p;
HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));//0号不启用
HT[0].weight=999;//默认0号为最大权值,为上面的min1,min2的默认值
for(p=HT+1,i=1;i<=n;i++,p++,w++) //将n个字符所对应的单个根节点赋予权值
{ p->lchild=p->rchild=p->parent=0;
p->weight=w->weight;
p->c=w->c;
}
for(;i<=m;i++) //将剩下的分支节点置为空
p->lchild=p->rchild=p->parent=p->weight=0;
for(i=n+1;i<=m;i++) //建立赫夫曼树
{ Select(HT,i-1,s1,s2); //选出两个最小的节点
HT[s1].parent=HT[s2].parent=i;
HT[i].lchild=s1;HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight; //权值合并为一个新节点
HT[i].parent=0;
}
return 1;
}
3.求出每个字符所对应的赫夫曼编码,创建编码表
int CreateTable(HuffmanCode &HC,HuffmanTree HT,int n) //创建编码表 对每个字符进行编码
{ HC=(HuffmanCode)malloc((n+1)*sizeof(char *));
char *cd=(char *)malloc(n*sizeof(char));
cd[n-1]='\0';
int start,c,i,f;
for(i=1;i<=n;++i)
{ start=n-1; //编码结束符位置
for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)
if(HT[f].lchild==c) cd[--start]='0'; //左分支设置0右分支设置1
else cd[--start]='1';
HC[i]=(char *)malloc((n-start)*sizeof(char));
strcpy(HC[i],&cd[start]);
}
free(cd);
return 1;
}
如下面题目要求示例:
1、初始化(Init):能够对输入的任意长度的字符串s进行统计,统计每个字符的频度,并建立哈夫曼树
2、建立编码表(CreateTable):利用已经建好的哈夫曼树进行编码,并将每个字符的编码输出。
3、编码(Encoding):根据编码表对输入的字符串进行编码,并将编码后的字符串输出。
4、译码(Decoding):利用已经建好的哈夫曼树对编码后的字符串进行译码,并输出译码结果。
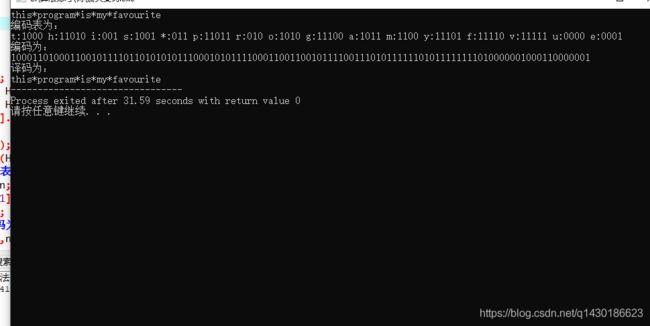
下面给出完整代码及运行结果
#include