数据结构——课程设计
课程设计报告
题 目 数据结构课程设计
学生姓名
学 号
院 系 计算机与软件学院
专 业 信息安全
指导教师
二O二一年十二月二十四日
目 录
一、 任务概述········································5
(一) 栈的应用——后缀表达式实现··································5
(二) 图的应用——最小生成树······································5
(三) 图的应用——活动图··········································5
(四) 堆排序的应用——Top K问题···································6
二、 算法设计思想····································6
(一) 栈的应用——后缀表达式实现··································6
(二) 图的应用——最小生成树······································6
(三) 图的应用——活动图··········································7
(四) 堆排序的应用——Top K问题···································7
三、 测试结果········································8
(一) 栈的应用——后缀表达式实现··································8
(二) 图的应用——最小生成树······································8
(三) 图的应用——活动图··········································9
(四) 堆排序的应用——Top K问题··································10
参考文献·············································10
附件·················································11
数据结构课程设计
摘要:本文主要介绍了数据结构中的栈、图和堆排序在具体案例中的应用:利用栈的存储结构实现了中缀表达式的后缀表示,基于最小生成树算法实现了无向网中代价最小的路线求解,利用AOE-网求解关键路径并估算某开发项目的完成时间,最后利用堆排序算法解决Top K问题。本文针对这些具体案例,有效地组织、存储和处理数据,正确地改进或设计满足功能需求的算法,旨在通过实际应用案例,提升数据结构和算法的编程实现能力,增加系统全面的实践经历。
关键词:数据结构;栈 ;图 ;堆排序
Course design of data structure
Abstract:This paper mainly introduces the application of stack, graph and heap sorting in data structure in specific cases: the suffix representation of infix expression is realized by using the storage structure of stack, the route with the lowest cost in undirected network is solved based on the minimum spanning tree algorithm, the critical path is solved by AOE network, and the completion time of a development project is estimated, Finally, the heap sorting algorithm is used to solve the top k problem. Aiming at these specific cases, this paper effectively organizes, stores and processes data, and correctly improves or designs algorithms to meet functional requirements. The purpose is to improve the programming ability of data structure and algorithms and increase the comprehensive practical experience of the system through practical application cases.
Key words:Data structure Stack Diagram Sorting
一、任务概述
(一)栈的应用——后缀表达式实现
利用一个栈,实现中缀表达式的后缀表示。例如,输入a+c/d*(e-f)#,输出acd/ef-*+。其中#为表达式结束标志。要求,栈底元素为#,每次对栈操作时,均应打印输出当前栈内情况。
(二)图的应用——最小生成树
基于最小生成树算法(两种典型算法可任选一种或两种实现),求解无向有权图中代价最小的路线,打印输出结果。 请自行选择图的存储结构。
测试用图如图1.2.1,1.2.2:

图1.2.1 图1.2.2
(三)图的应用——活动图
图的应用。一个软件开发项目的活动图如下所示,弧上的数值为需要的开发天数。请用邻接表实现该图的存储。(1)计算输出每条弧最早发生时间和最迟发生时间;(2)输出该开发项目的最短开发周期;(2)输出一旦延期将影响开发进度的全部路径。如图1.3.1
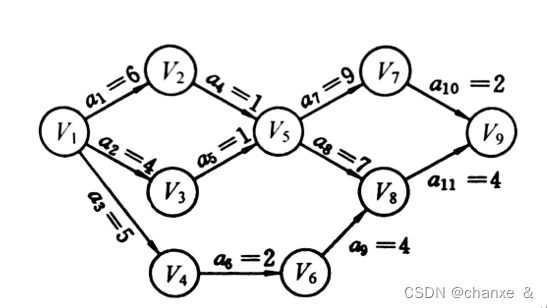
图1.3.1
(四)堆排序的应用——Top K问题
以任务3中的图为测试例子,定义有向边结构体(弧尾,弧头,权值),用弧的结构体数组保存全部弧,并针对该数组,实现堆排序算法,并用其解决Top K排序问题。(2次课)
Top K排序:查找最大的(或最小的)K个元素。
要求分析算法时间复杂度,讨论哪些算法适合TopK排序问题,简述理由。
注意,算法应允许通过参数设置,选择最大K还是最小K个元素;
二、算法设计思想
(一)栈的应用——后缀表达式实现
1.遇到操作数:直接输出(添加到后缀表达式中);
2.栈为空时,遇到运算符,直接入栈;
3.遇到左括号:将其入栈;
4.遇到右括号:执行出栈操作,并将出栈的元素输出,直到弹出栈的是左括号,左括号不输出;
5.遇到其他运算符:加减乘除:弹出所有优先级大于或者等于该运算符的栈顶元素,然后将该运算符入栈;
6.最终将栈中的元素依次出栈,输出。
(二) 图的应用——最小生成树
Prim(普里姆)算法:
算法思想 —— 归并顶点
1.在图中任取一个顶点K作为开始点。令U={k},W=V-U,其中V为图中所有顶点的集合;
2.在U中选取一个顶点,W中选取另一个顶点,使二者对应的边是最短的一条。将该边作为最小生成树的边保存起来,并将该边顶点全部加入U集合中,并从W中删去这些顶点;
3.重新调整U中顶点到W中顶点的距离, 使之保持最小,再重复此过程,直到W为空集止。
(三) 图的应用——活动图
1)要找出一个AOE网中的关键路径,就要先找出网里的关键活动,这些关键活动间的路径就是关键路径。
2)判断一个活动是不是关键活动,方法是要先找到所有活动的最早开始时间和最晚开始时间,并且对它们进行比较,如果二者相等(意味着这个活动在该工程中没有时间松动),说明这个活动是关键活动。
3)对于活动

图2.3.1
注意,这里假设顶点下标从0开始,所以Vi==0,则表示它是源点,因此最早的开始时间为0;当某个顶点不是源点,那么只有在它前面的事件都发生完后,才能轮到这个事件,所以用了max。
4)对于活动

图2.3.2
(四) 堆排序的应用——Top K问题
- 采用顺序表存储表示。
- 建堆:从最后一个非叶子结点开始,反复筛选。
- 筛选:
step 1 得到堆顶元素后,交换堆顶和最后一个元素,此时根结点的左右子树均为堆; step 2 自上而下重新调整为大顶堆:首先以堆顶元素和左右子树根节点的值进行比较,若堆顶元素小,则与左右根节点中值较大的交换,重复该步骤直至叶子结点;
step 3 重复上述过程直至结束。 - Top K 问题:设置函数参数flag供选择查找最大或最小k个元素,利用堆排序结果
输出最大或最小k个元素。 - 时间复杂度分析:对深度为k的堆,筛选算法中关键字比较次数最多2(k-1)次,故在建立含n个元素,深度为h的堆时,关键字总的比较次数不超过4n。而n个结点的完全二叉树深度为(log2(n)+1)向下取整,调整建新堆时调用heapadjust过程(n-1)次,总比较次数不超过2n(log2(n)),故堆排序在最坏情况下时间复杂度为O(nlogn)。
- Top K排序问题宜采用算法及理由:
堆排序:用一个小顶堆维护大小为k的数组,时间复杂度为O(nlogk),该算法不需要一次将原数组中的内容全部加载到内存中,可以处理较大的数据量。
快速排序:利用找分割点的方法,时间复杂度低。
三、测试结果
(一)栈的应用——后缀表达式实现
图3.1.1
(二)图的应用——最小生成树
图3.2.1
图3.2.2
(三)图的应用——活动图
图3.3.1
如图3.4.1
图3.4.1
参考文献:
【1】 CSDN 博主遐光 《中缀表达式转后缀表达式算法思想》
【2】 CSDN 博主糖不苦z的原创文章
https://blog.csdn.net/weixin_44203971/article/details/103934109
【3】 程杰《大话数据结构》 清华大学出版社 图
【4】 CSDN博主「feliciafay」的原创文章
https://blog.csdn.net/feliciafay/article/details/12252727
【5】 严蔚敏 吴伟民.《数据结构(C语音版)》清华大学出版社
附件:
(一)栈的应用——后缀表达式实现
代码:
#include
typedef struct{
char data[50];
int top;
}Stack,*S_ptr;
void InitStack(S_ptr S){//初始化栈
for(int i=0;i<50;i++){
S->data[i]='\0';
}
S->top=-1;
}
void Push(S_ptr S,char c){//压入栈中
printf("%c入栈\n",c);
if(S->top==49){
printf("栈满\n");
return ;
}
S->top++;
S->data[S->top]=c;
return ;
}
void Pop(S_ptr S,char &c){//弹出栈
if(S->top==-1){
printf("栈空\n");
return;
}
c=S->data[S->top];
printf("%c出栈\n",c);
S->top--;
return;
}
char gettop(S_ptr S){
if(S->top==-1){
return '\0';
}
return S->data[S->top];
}
void OutputStack(S_ptr S,int top)
{
int i;
for(i=top;i>=0;i--)
{
printf("%c",S->data[i]);
printf("\n");
}
}
int main(){
Stack s;
S_ptr S=&s;
InitStack(S);
char e;
char a[100];
printf("请输入中缀表达式:");
gets(a);
Push(S,'#');//栈底元素为#
for(int i=0;a[i]!='#';i++){
if(a[i]!='+'&&a[i]!='-'&&a[i]!='*'&&a[i]!='/'&&a[i]!='('&&a[i]!=')') {printf("打印%c\n",a[i]);printf("此时栈状态:\n");OutputStack( S,S->top);}//非操作数直接输出
else if(a[i]==')'){
while(gettop(S)!='('&&gettop(S)!='\0'){//括号匹配
Pop(S,e);
printf("%c\n",e);
printf("此时栈状态:\n");
OutputStack( S,S->top);
}
Pop(S,e);}
else if(a[i]=='+'||a[i]=='-'){
if(gettop(S)=='*'||gettop(S)=='/'){
while(gettop(S)!='('&&gettop(S)!='#'){
Pop(S,e);
printf("打印%c\n",e);
printf("此时栈状态:\n");
OutputStack( S,S->top);
}
Push(S,a[i]);
printf("此时栈状态:\n");
OutputStack( S,S->top);
}
else {Push(S,a[i]);printf("此时栈状态:\n");
OutputStack( S,S->top);}
}
else if(a[i]=='*'||a[i]=='/'){
if(gettop(S)=='*'||gettop(S)=='/'){
Pop(S,e);
printf("打印%c\n",e);
printf("此时栈状态:\n");
OutputStack( S,S->top);
Push(S,a[i]);
printf("此时栈状态:\n");
OutputStack( S,S->top);
}
else {Push(S,a[i]);printf("此时栈状态:\n");
OutputStack( S,S->top);}
}
else {Push(S,a[i]);printf("此时栈状态:\n");
OutputStack( S,S->top);}
}
while(S->data[S->top]!='#'){//将剩余的运算符号出栈
Pop(S,e);
printf("打印%c\n",e);
printf("此时栈状态:\n");
OutputStack( S,S->top);
}
return 0;
}数据:a+b#
(二) 图的应用——最小生成树
代码:
//2.图的应用——最小生成树
#include
#include
using namespace std;
#define max_vertex_num 20
int max_weight=0;//记录无向带权图中最大权值
typedef struct edgenode{//边
int adjvex;//该边所指向的顶点位置
edgenode *nextedge;//指向下一条边的指针
int weight;//边上的权值
}edgenode;
typedef struct vnode{//顶点
int data;//顶点信息
edgenode *firstedge;//指向第一条依附该顶点的指针
}vnode,adjlist[max_vertex_num];
typedef struct{//图
adjlist vertices;//顶点向量
int vexnum,edgenum;//图的当前顶点数和边数
}graph;
typedef struct node{//辅助数组,记录已访问的顶点及与其相连的边中最小的权值
int adjvex;
int lowcost;
}node;
node closedge[max_vertex_num];
//查找顶点val在顶点向量中的位置
int local(graph G,int val)
{
for(int i=0;i>G.vexnum>>G.edgenum;
for(int i=0,j=0;i>v1>>v2>>weights;
i=local(G,v1);//查找两顶点在顶点向量中的位置
j=local(G,v2);
if(G.vertices[i].firstedge==NULL)
{
e=new edgenode;//新建边结点
e->adjvex=j;
e->nextedge=NULL;
e->weight=weights;
if(e->weight>max_weight)//寻找最大权值
max_weight=e->weight;
G.vertices[i].firstedge=e;//将该边结点接入第i个链表
}
else
{
p=G.vertices[i].firstedge;
while(p->nextedge!=NULL)//循环后移p指针,使其指向第i个链表中的最后一个结点
{
p=p->nextedge;
}
e=new edgenode;//新建边结点
e->adjvex=j;
e->nextedge=NULL;
e->weight=weights;
if(e->weight>max_weight)//寻找最大权值
max_weight=e->weight;
p->nextedge=e;//将该边结点接入第i个链表的末尾
}
if(G.vertices[j].firstedge==NULL)
{
e=new edgenode;
e->adjvex=i;
e->nextedge=NULL;
e->weight=weights;
G.vertices[j].firstedge=e;//将该边结点接入第i个链表
}
else
{
q=G.vertices[j].firstedge;
while(q->nextedge!=NULL)//循环后移p指针,使其指向第i个链表中的最后一个结点
{
q=q->nextedge;
}
e=new edgenode;
e->adjvex=i;
e->nextedge=NULL;
e->weight=weights;
q->nextedge=e;//将该边结点接入第i个链表的末尾
}
}
max_weight++;
for(i=0;iclosedge[i].lowcost)
{
min=closedge[i].lowcost;
result=i;
}
}
return result;
}
//用普里姆算法从第u个顶点出发构造无向有权图G的最小生成树T并输出代价最小的路线
void minispantree_prim(graph G,int u)
{
int i,j,k,t1,t2;
edgenode *p=NULL;
k=local(G,u);
p=G.vertices[k].firstedge;
while(p)//与顶点u相连的边的权值和顶点输入辅助数组closedge[]
{
i=p->adjvex;
closedge[i].adjvex=u;
closedge[i].lowcost=p->weight;
p=p->nextedge;
}
closedge[k].lowcost=0;//访问过的顶点的边的权值标记为0
for(i=1;i"<adjvex;
if(closedge[j].lowcost>p->weight)//与上一顶点比较,输入权值小的边的权值和与其相连接的顶点
{
closedge[j].adjvex=G.vertices[k].data;
closedge[j].lowcost=p->weight;
}
p=p->nextedge;
}
}
}
int main()
{
graph G;
creatUDG(G);
cout<>u;
cout<<"代价最小的路线为:"<
#include
#include
#include
typedef int DataType; /*栈元素类型定义*/
#define MaxSize 50 /*最大顶点个数*/
#define StackSize 100
typedef struct
{
DataType stack[StackSize];
int top;
}SeqStack;
void InitStack(SeqStack *S)
/*将栈初始化为空栈只需要把栈顶指针top置为0*/
{
S->top=0; /*把栈顶指针置为0*/
}
int StackEmpty(SeqStack S)
/*判断栈是否为空,栈为空返回1,否则返回0*/
{
if(S.top==0) /*判断栈顶指针top是否为0*/
return 1; /*当栈为空时,返回1;否则返回0*/
else
return 0;
}
int GetTop(SeqStack S, DataType *e)
/*取栈顶元素。将栈顶元素值返回给e,并返回1表示成功;否则返回0表示失败。*/
{
if(S.top<=0) /*在取栈顶元素之前,判断栈是否为空*/
{
printf("栈已经空!\n");
return 0;
}
else
{
*e=S.stack[S.top-1]; /*在取栈顶元素*/
return 1;
}
}
int PushStack(SeqStack *S,DataType e)
/*将元素e进栈,元素进栈成功返回1,否则返回0.*/
{
if(S->top>=StackSize) /*在元素进栈前,判断是否栈已经满*/
{
printf("栈已满,不能进栈!\n");
return 0;
}
else
{
S->stack[S->top]=e; /*元素e进栈*/
S->top++; /*修改栈顶指针*/
return 1;
}
}
int PopStack(SeqStack *S,DataType *e)
/*出栈操作。将栈顶元素出栈,并将其赋值给e。出栈成功返回1,否则返回0*/
{
if(S->top<=0) /*元素出栈之前,判断栈是否为空*/
{
printf("栈已经没有元素,不能出栈!\n");
return 0;
}
else
{
S->top--; /*先修改栈顶指针,即出栈*/
*e=S->stack[S->top]; /*将出栈元素赋值给e*/
return 1;
}
}
int StackLength(SeqStack S)
/*求栈的长度,即栈中元素个数,栈顶指针的值就等于栈中元素的个数*/
{
return S.top;
}
void ClearStack(SeqStack *S)
/*将栈初始化为空栈只需要把栈顶指针top置为0*/
{
S->top=0; /*把栈顶指针置为0*/
}
/*图的邻接表类型定义*/
typedef char VertexType[4];
typedef int InfoPtr; /*定义为整型,为了存放权值*/
typedef int VRType;
typedef enum{DG,DN,UG,UN}GraphKind; /*图的类型:有向图、有向网、无向图和无向网*/
typedef struct ArcNode /*边结点的类型定义*/
{
int adjvex; /*弧指向的顶点的位置*/
InfoPtr *info; /*弧的权值*/
struct ArcNode *nextarc; /*指示下一个与该顶点相邻接的顶点*/
}ArcNode;
typedef struct VNode /*头结点的类型定义*/
{
VertexType data; /*用于存储顶点*/
ArcNode *firstarc; /*指示第一个与该顶点邻接的顶点*/
}VNode,AdjList[MaxSize];
typedef struct /*图的类型定义*/
{
AdjList vertex;
int vexnum,arcnum; /*图的顶点数目与弧的数目*/
GraphKind kind; /*图的类型*/
}AdjGraph;
int ve[MaxSize]; /*ve存放事件最早发生时间*/
int TopologicalOrder(AdjGraph N,SeqStack *T)
/*采用邻接表存储结构的有向网N的拓扑排序,并求各顶点对应事件的最早发生时间ve*/
/*如果N无回路,则用用栈T返回N的一个拓扑序列,并返回1,否则为0*/
{
int i,k,count=0;
int indegree[MaxSize]; /*数组indegree存储各顶点的入度*/
SeqStack S;
ArcNode *p;
/*将图中各顶点的入度保存在数组indegree中*/
for(i=0;iadjvex;
indegree[k]++;
p=p->nextarc;
}
}
InitStack(&S); /*初始化栈S*/
for(i=0;inextarc) /*处理编号为i的顶点的每个邻接点*/
{
k=p->adjvex; /*顶点序号为k*/
if(--indegree[k]==0) /*如果k的入度减1后变为0,则将k入栈S*/
PushStack(&S,k);
if(ve[i]+*(p->info)>ve[k]) /*计算顶点k对应的事件的最早发生时间*/
ve[k]=ve[i]+*(p->info);
}
}
if(countvalue)
value=ve[i]; /*value为事件的最早发生时间的最大值*/
for(i=0;inextarc)
/*弹出栈T的元素,赋给j,p指向j的后继事件k*/
{
k=p->adjvex;
dut=*(p->info); /*dut为弧的权值*/
if(vl[k]-dutnextarc)
{
k=p->adjvex;
dut=*(p->info); /*dut为弧的权值*/
e=ve[j]; /*e就是活动的最早开始时间*/
l=vl[k]-dut; /*l就是活动的最晚开始时间*/
printf("%s→%s %3d %3d %3d\n",N.vertex[j].data,N.vertex[k].data,e,l,l-e);
if(e==l) /*将关键活动保存在数组中*/
{
e1[count]=j;
e2[count]=k;
count++;
}
}
printf("输出该开发项目的最短开发周期:%d\n",ve[N.vexnum-1]);
printf("计算输出每条弧最早发生时间和最迟发生时间:");
for(k=0;kvexnum);
for(i=0;ivexnum;i++) /*将顶点存储在头结点中*/
{
scanf("%s",N->vertex[i].data);
N->vertex[i].firstarc=NULL; /*将相关联的顶点置为空*/
}
printf("请输入弧尾、弧头和权值(以空格作为分隔):\n");
for(k=0;karcnum;k++) /*建立边链表*/
{
scanf("%s%s%*c%d",v1,v2,&w);
i=LocateVertex(*N,v1);
j=LocateVertex(*N,v2);
/*j为弧头i为弧尾创建邻接表*/
p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=j;
p->info=(InfoPtr*)malloc(sizeof(InfoPtr));
*(p->info)=w;
/*将p指向的结点插入到边表中*/
p->nextarc=N->vertex[i].firstarc;
N->vertex[i].firstarc=p;
}
(*N).kind=DN;
}
void DestroyGraph(AdjGraph *N)
/*销毁无向图G*/
{
int i;
ArcNode *p,*q;
for(i=0;ivexnum;++i) /*释放网中的边表结点*/
{
p=N->vertex[i].firstarc; /*p指向边表的第一个结点*/
if(p!=NULL) /*如果边表不为空,则释放边表的结点*/
{
q=p->nextarc;
free(p);
p=q;
}
}
(*N).vexnum=0; /*将顶点数置为0*/
(*N).arcnum=0; /*将边的数目置为0*/
}
int main()
{
AdjGraph N;
CreateGraph(&N); /*采用邻接表存储结构创建有向网N*/
CriticalPath(N); /*求网N的关键路径*/
DestroyGraph(&N); /*销毁网N*/
}
实验数据:
请输入图的顶点数,边数(以逗号分隔): 8,10
请输入8个顶点的值:v1 v2 v3 v4 v5 v6 v7 v8
请输入弧尾、弧头和权值(以空格作为分隔):
v1 v2 3
v1 v2 4
v1 v4 6
v2 v5 3
v4 v7 3
v3 v5 1
v5 v7 3
v6 v8 4
v7 v8 5
v5 v6 5
(四)堆排序的应用——Top K问题
实验代码:
//4.堆排序的应用——Top K问题
#include
#include
using namespace std;
#define max_arc_num 20
typedef struct arcnode{//弧(有向边结构体)
string head,tail;//弧头,弧尾
string weight;//弧上的权值
}arcnode;
//全局变量
arcnode arc[max_arc_num];//弧的结构体数组
int arclen=0;//数组长度
//输入各条弧
void In_Put()
{
int i=1;
arc[0].tail="0";arc[0].head="0";arc[0].weight="0";//数组零号元素不存储弧 ,用于交换 记录过程中暂存记录
cout<<"请输入各条弧的弧尾,弧头,权值(-1表示结束输入):"<>arc[i].tail&&arc[i].tail!="-1")
{
cin>>arc[i].head>>arc[i].weight;
i++;
}
arclen=i-1;
}
//已知arc[s...m]中除arc[s]外均满足堆的特征,自上而下调整,使arc[s...m]也成为一个大顶堆
void heapadjust(arcnode arcs[],int s,int m)
{
arcs[0]=arcs[s];
for(int j=2*s;j<=m;j*=2)//沿着权值较大的孩子节点向下筛选
{
if(j=arcs[j].weight)//根和子树根之间相互比较
break;//找到arc[0]的插入位置,无需继续往下调整
arcs[s]=arcs[j];//否则记录上移,尚需继续往下调整
s=j;
}
arcs[s]=arcs[0];
}
// 对弧的结构体数组进行堆排序
void heapsort(arcnode arcs[])
{
for(int i=arclen;i>0;--i)
heapadjust(arcs,i,arclen);//建大顶堆(自下而上)
for(int i=arclen;i>1;--i)//将堆顶记录和当前未经排序子序列arc[1...i]中最后一个记录相互交换
{
arcs[0]=arcs[i];
arcs[i]=arcs[1];
arcs[1]=arcs[0];
heapadjust(arcs,1,i-1); //对arc[1]进行筛选
}
}
//输出排序后的结果
void Out_Put()
{
cout<<"按弧的权值由小到大,输出各条有向弧(箭头由弧尾指向弧头):"<"<arclen-k;i--)
{
cout<"<"<>k;
cout<<"查找最大"<>flag;
Top_K(k,flag);
return 0;
}
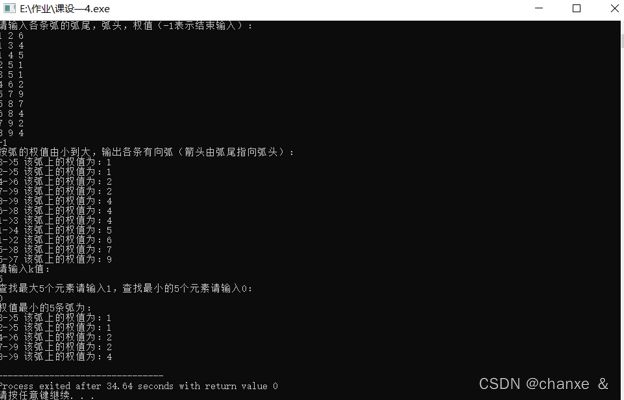
输入数据:
请输入各条弧的弧尾,弧头,权值(-1表示结束输入):
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4
-1
请输入k值:5
查找最大5个元素请输入1,查找最小的5个元素请输入0:0