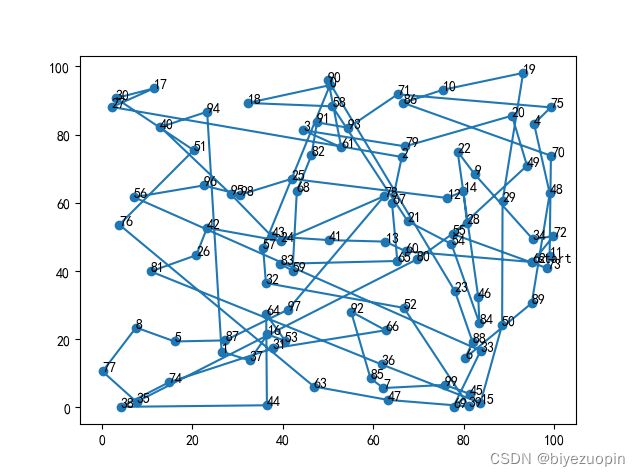
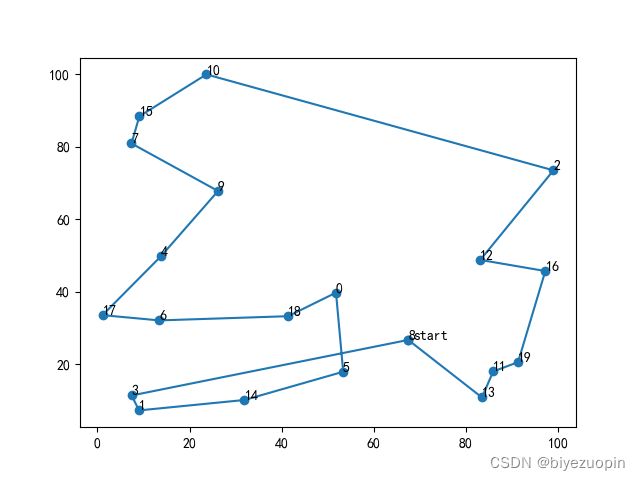
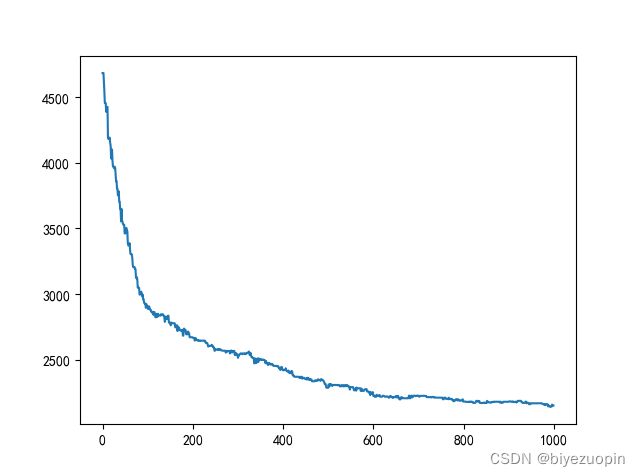
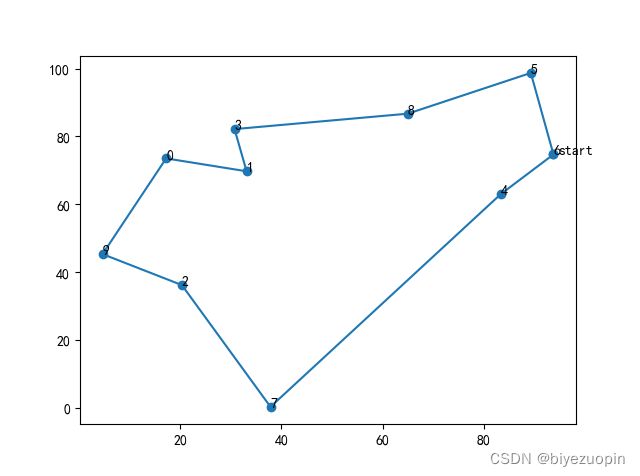
基于Python实现的遗传算法求TSP问题

遗传算法求TSP问题
目录
人工智能第四次实验报告 1
遗传算法求TSP问题 1
一 、问题背景 1
1.1 遗传算法简介 1
1.2 遗传算法基本要素 2
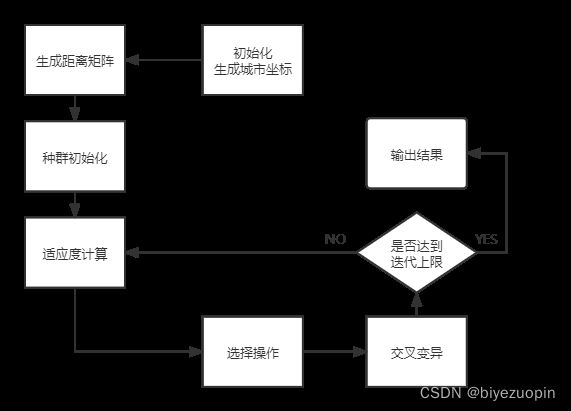
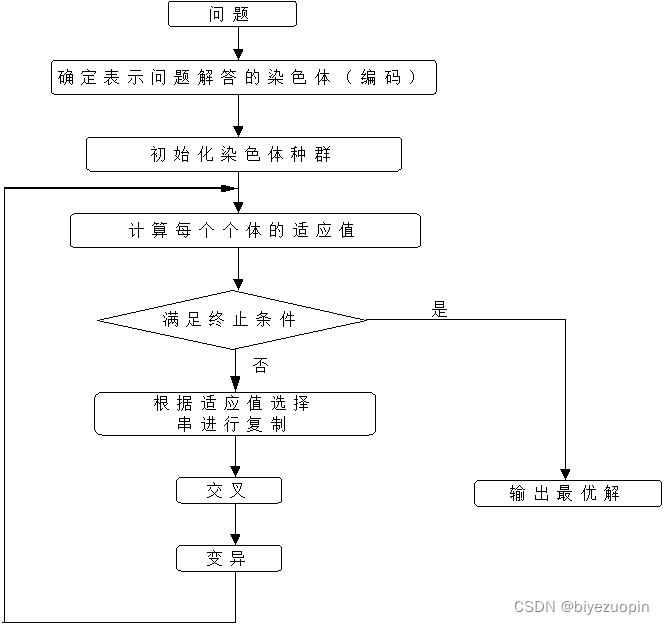
1.3 遗传算法一般步骤 2
二 、程序说明 3
2.3 选择初始群体 4
2.4 适应度函数 4
2.5 遗传操作 4
2.6 迭代过程 4
三 、程序测试 5
3.1 求解不同规模的TSP问题的算法性能 5
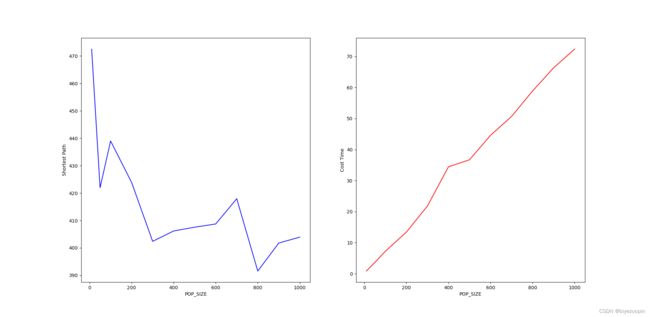
3.2 种群规模对算法结果的影响 5
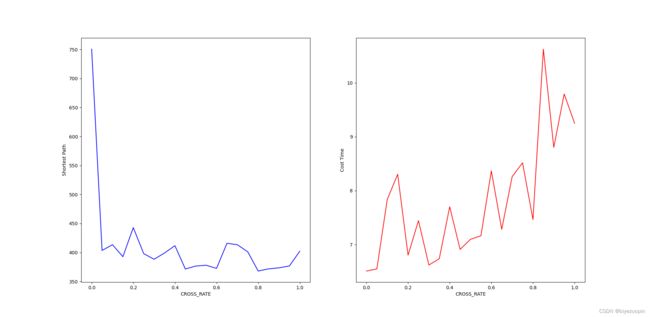
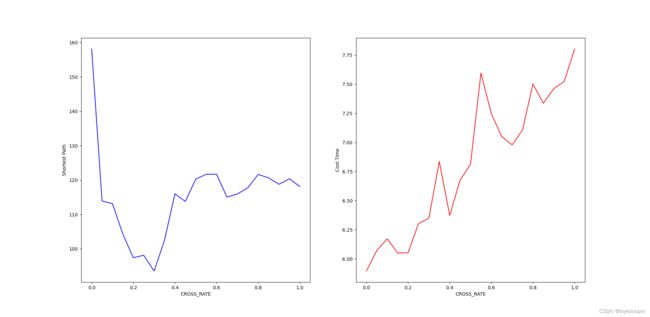
3.3 交叉概率对算法结果的影响 6
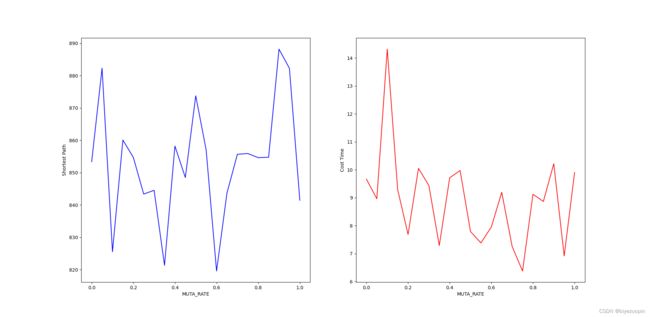
3.4 变异概率对算法结果的影响 7
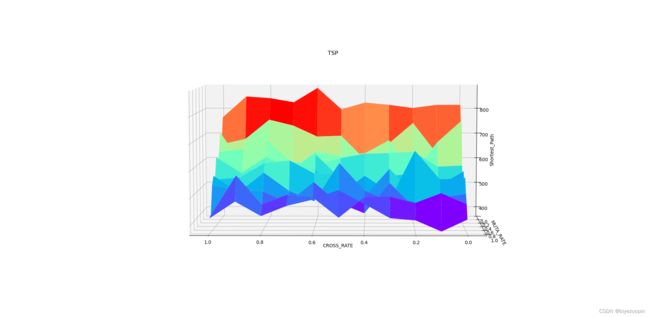
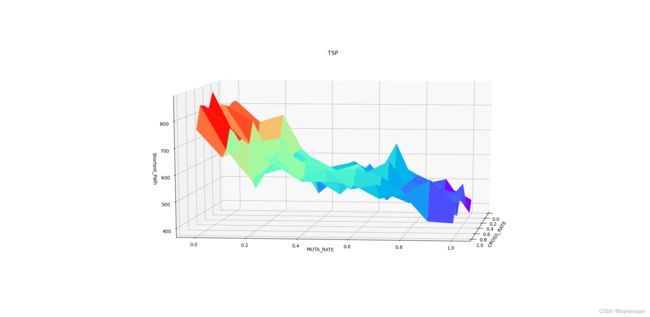
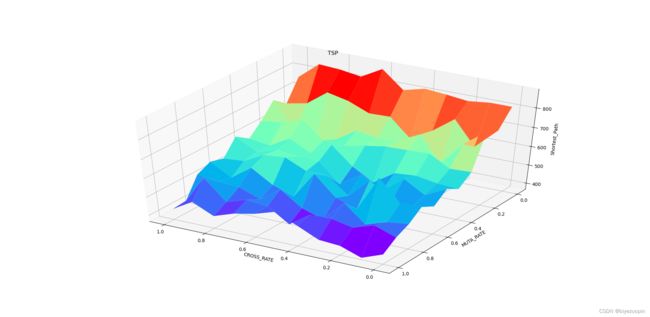
3.5 交叉概率和变异概率对算法结果的影响 7
四 、算法改进 8
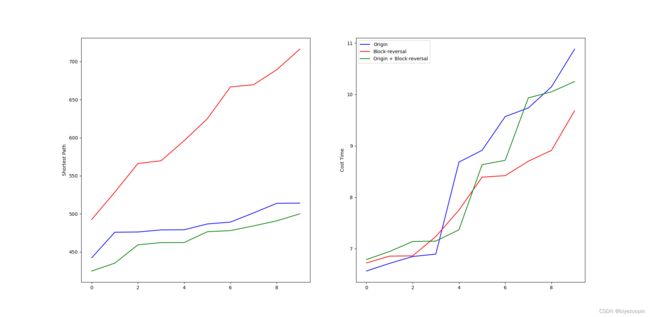
4.1 块逆转变异策略 8
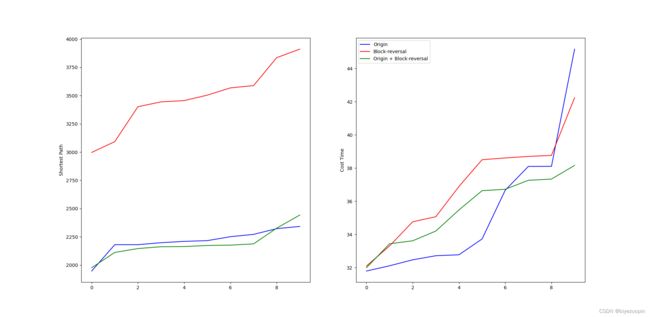
4.2 锦标赛选择法 9
五 、实验总结 10
一 、问题背景
1.1遗传算法简介
遗传算法是一种进化算法，基于自然选择和生物遗传等生物进化机制的一种搜索算法，其通过选 择、重组和变异三种操作实现优化问题的求解。它的本质是从原问题的一组解出发改进到另一组较好的 解，再从这组改进的解出发进一步改进。在搜索过程中，它利用结构和随机的信息，是满足目标的决策 获得最大的生存可能，是一种概率型算法。
遗传算法主要借用生物中“适者生存”的原则，在遗传算法中，染色体对应的是数据或数组，通常由 一维的串结构数据来表示。串上的各个位置对应一个基因座，而各个位置上所取的值对等位基因。遗传 算法处理的是基因型个体，一定数量的个体组成了群体。群体的规模就是个体的数目。不同个体对环境 的适应度不同，适应度打的个体被选择进行遗传操作产生新个体。本文转载自http://www.biyezuopin.vip/onews.asp?id=16719每次选择两个染色体进行产生一组新 染色体，染色体也可能发生变异，得到下一代群体。
1.2遗传算法基本要素
1.参数编码：可以采用位串编码、实数编码、多参数级联编码等
2.设定初始群体：
1.启发 / 非启发给定一组解作为初始群体
2.确定初始群体的规模
3.设定适应度函数：将目标函数映射为适应度函数，可以进行尺度变换来保证非负、归一等特性
4.设定遗传操作：
1.选择：从当前群体选出一系列优良个体，让他们产生后代个体
2.交叉：两个个体的基因进行交叉重组来获得新个体
3.变异：随机变动个体串基因座上的某些基因
5.设定控制参数：例如变异概率、交叉程度、迭代上限等。

import numpy as np
import random
import matplotlib.pyplot as plt
import copy
import time

from matplotlib.ticker import MultipleLocator
from scipy.interpolate import interpolate

CITY_NUM = 20
City_Map = 100 * np.random.rand(CITY_NUM, 2)

DNA_SIZE = CITY_NUM     #编码长度
POP_SIZE = 100          #种群大小
CROSS_RATE = 0.6        #交叉率
MUTA_RATE = 0.2         #变异率
Iterations = 1000       #迭代次数

# 根据DNA的路线计算距离
def distance(DNA):
    dis = 0
    temp = City_Map[DNA[0]]
    for i in DNA[1:]:
        dis = dis + ((City_Map[i][0]-temp[0])**2+(City_Map[i][1]-temp[1])**2)**0.5
        temp = City_Map[i]
    return dis+((temp[0]-City_Map[DNA[0]][0])**2+(temp[1]-City_Map[DNA[0]][1])**2)**0.5

# 计算种群适应度，这里适应度用距离的倒数表示
def getfitness(pop):
    temp = []
    for i in range(len(pop)):
        temp.append(1/(distance(pop[i])))
    return temp-np.min(temp) + 0.000001

# 选择：根据适应度选择，以赌轮盘的形式，适应度越大的个体被选中的概率越大
def select(pop, fitness):
    s = fitness.sum()
    temp = np.random.choice(np.arange(len(pop)), size=POP_SIZE, replace=True,p=(fitness/s))
    p = []
    for i in temp:
        p.append(pop[i])
    return p

# 4.2 选择：锦标赛选择法
def selectII(pop, fitness):
    p = []
    for i in range(POP_SIZE):
        temp1 = np.random.randint(POP_SIZE)
        temp2 = np.random.randint(POP_SIZE)
        DNA1 = pop[temp1]
        DNA2 = pop[temp2]
        if fitness[temp1] > fitness[temp2]:
            p.append(DNA1)
        else:
            p.append(DNA2)
    return p

# 变异：选择两个位置互换其中的城市编号
def mutation(DNA, MUTA_RATE):
    if np.random.rand() < MUTA_RATE: # 以MUTA_RATE的概率进行变异
        # 随机产生两个实数，代表要变异基因的位置，确保两个位置不同，将2个所选位置进行互换
        mutate_point1 = np.random.randint(0, DNA_SIZE)
        mutate_point2 = np.random.randint(0,DNA_SIZE)
        while(mutate_point1 == mutate_point2):
            mutate_point2 = np.random.randint(0,DNA_SIZE)
        DNA[mutate_point1],DNA[mutate_point2] = DNA[mutate_point2],DNA[mutate_point1]

# 4.1 变异：在父代中随机选择两个点，然后反转之间的部分
def mutationII(DNA, MUTA_RATE):
    if np.random.rand() < MUTA_RATE:
        mutate_point1 = np.random.randint(0, DNA_SIZE)
        mutate_point2 = np.random.randint(0, DNA_SIZE)
        while (mutate_point1 == mutate_point2):
            mutate_point2 = np.random.randint(0, DNA_SIZE)
        if(mutate_point1 > mutate_point2):
            mutate_point1, mutate_point2 = mutate_point2, mutate_point1
        DNA[mutate_point1:mutate_point2].reverse()

# 4.1 变异：调用 I 和 II
def mutationIII(DNA, MUTA_RATE):
    mutationII(DNA, MUTA_RATE)
    mutation(DNA, MUTA_RATE)

# 交叉变异
# muta = 1时变异调用 mutation；
# muta = 2时变异调用 mutationII；
# muta = 3时变异调用 mutationIII
def crossmuta(pop, CROSS_RATE, muta=1):
    new_pop = []
    for i in range(len(pop)):   # 遍历种群中的每一个个体，将该个体作为父代
        n = np.random.rand()
        if n >= CROSS_RATE:     # 大于交叉概率时不发生变异，该子代直接进入下一代
            temp = pop[i].copy()
            new_pop.append(temp)
        # 小于交叉概率时发生变异
        if n < CROSS_RATE:
            # 选取种群中另一个个体进行交叉
            list1 = pop[i].copy()
            list2 = pop[np.random.randint(POP_SIZE)].copy()
            status = True
            # 产生2个不相等的节点，中间部分作为交叉段，采用部分匹配交叉
            while status:
                k1 = random.randint(0, len(list1) - 1)
                k2 = random.randint(0, len(list2) - 1)
                if k1 < k2:
                    status = False

            k11 = k1

            # 两个DNA中待交叉的片段
            fragment1 = list1[k1: k2]
            fragment2 = list2[k1: k2]

            # 交换片段后的DNA
            list1[k1: k2] = fragment2
            list2[k1: k2] = fragment1

            # left1就是 list1除去交叉片段后剩下的DNA片段
            del list1[k1: k2]
            left1 = list1

            offspring1 = []
            for pos in left1:
                # 如果 left1 中有与待插入的新片段相同的城市编号
                if pos in fragment2:
                    # 找出这个相同的城市编号在在原DNA同位置编号的位置的城市编号
                    # 循环查找，直至这个城市编号不再待插入的片段中
                    pos = fragment1[fragment2.index(pos)]
                    while pos in fragment2:
                        pos = fragment1[fragment2.index(pos)]
                    # 修改原DNA片段中该位置的城市编号为这个新城市编号
                    offspring1.append(pos)
                    continue
                offspring1.append(pos)
            for i in range(0, len(fragment2)):
                offspring1.insert(k11, fragment2[i])
                k11 += 1
            temp = offspring1.copy()
            # 根据 type 的值选择一种变异策略
            if muta == 1:
                mutation(temp, MUTA_RATE)
            elif muta == 2:
                mutationII(temp, MUTA_RATE)
            elif muta == 3:
                mutationIII(temp, MUTA_RATE)
            # 把部分匹配交叉后形成的合法个体加入到下一代种群
            new_pop.append(temp)

    return new_pop

def print_info(pop):
    fitness = getfitness(pop)
    maxfitness = np.argmax(fitness)     # 得到种群中最大适应度个体的索引
    print("最优的基因型：", pop[maxfitness])
    print("最短距离：",distance(pop[maxfitness]))
    # 按最优结果顺序把地图上的点加入到best_map列表中
    best_map = []
    for i in pop[maxfitness]:
        best_map.append(City_Map[i])
    best_map.append(City_Map[pop[maxfitness][0]])
    X = np.array((best_map))[:,0]
    Y = np.array((best_map))[:,1]
    # 绘制地图以及路线
    plt.figure()
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.scatter(X,Y)
    for dot in range(len(X)-1):
        plt.annotate(pop[maxfitness][dot],xy=(X[dot],Y[dot]),xytext = (X[dot],Y[dot]))
    plt.annotate('start',xy=(X[0],Y[0]),xytext = (X[0]+1,Y[0]))
    plt.plot(X,Y)

# 3.2 种群规模对算法结果的影响
def pop_size_test():
    global POP_SIZE
    ITE = 3 # 每个值测试多次求平均数以降低随机误差
    i_list = [10, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000]
    b_list = []
    t_list = []
    for i in i_list:
        print(i)
        POP_SIZE = i
        time_cost = 0
        min_path = 0
        for j in range(ITE):
            time_start = time.time()
            ans = tsp_solve()
            min_path += min(ans)
            time_end = time.time()
            time_cost += time_end - time_start

        b_list.append(min_path / ITE)
        t_list.append(time_cost / ITE)
    show_test_result(i_list, b_list, t_list, "POP_SIZE")

# 3.3 交叉概率对算法结果的影响
def cross_rate_test():
    global CROSS_RATE
    ITE = 3 # 每个值测试多次求平均数以降低随机误差
    i_list = range(0, 21)
    b_list = []
    t_list = []
    ii_list = [] # [0, 0.05, 0.1, ... 0.95, 1]
    for i in i_list:
        print(i)
        CROSS_RATE = 0.05 * i
        ii_list.append(CROSS_RATE)
        time_cost = 0
        min_path = 0
        for j in range(ITE):
            time_start = time.time()
            ans = tsp_solve()
            min_path += min(ans)
            time_end = time.time()
            time_cost += time_end - time_start

        b_list.append(min_path / ITE)
        t_list.append(time_cost / ITE)
    show_test_result(ii_list, b_list, t_list, "CROSS_RATE")

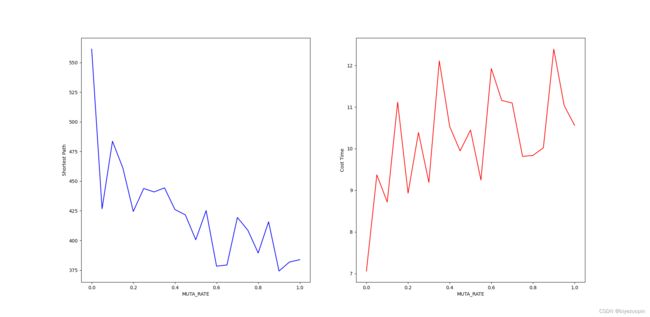
# 3.4 变异概率对算法结果的影响
def muta_rate_test():
    global MUTA_RATE
    ITE = 3 # 每个值测试多次求平均数以降低随机误差
    i_list = range(0, 21)
    b_list = []
    t_list = []
    ii_list = [] # [0, 0.05, 0.1, ... 0.95, 1]
    for i in i_list:
        print(i)
        MUTA_RATE = 0.05 * i
        ii_list.append(MUTA_RATE)
        time_cost = 0
        min_path = 0
        for j in range(ITE):
            time_start = time.time()
            ans = tsp_solve()
            min_path += min(ans)
            time_end = time.time()
            time_cost += time_end - time_start

        b_list.append(min_path / ITE)
        t_list.append(time_cost / ITE)
    show_test_result(ii_list, b_list, t_list, "MUTA_RATE")

# 3.5 交叉概率和变异概率对算法结果的影响
def cross_muta_test():
    s = np.array([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
    X, Y = np.meshgrid(s,s)
    Z = np.zeros(shape=(11, 11))

    global MUTA_RATE
    global CROSS_RATE
    for i in range(11):
        for j in range(11):
            print(str(i) + ":" + str(j))
            CROSS_RATE = X[0,i]
            MUTA_RATE = Y[0,j]
            ans = tsp_solve()
            Z[i, j] = min(ans)

    ax = plt.axes(projection='3d')
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1,cmap='rainbow', edgecolor='none')
    ax.set_xlabel("CROSS_RATE")
    ax.set_ylabel("MUTA_RATE")
    ax.set_zlabel("Shortest_Path")
    ax.set_title('TSP')
    plt.show()

# 3.2-3.4 生成参数测试结果的可视化图表
def show_test_result(i_list, b_list, t_list, msg):
    ax1 = plt.subplot(121)
    ax1.plot(i_list, b_list, 'b')
    ax1.set_xlabel(msg)
    ax1.set_ylabel("Shortest Path")

    ax2 = plt.subplot(122)
    ax2.plot(i_list, t_list, 'r')
    ax2.set_xlabel(msg)
    ax2.set_ylabel("Cost Time")
    plt.show()

# 求解TSP问题并返回最大值
# muta 指定变异方式，sel 指定选择方式
def tsp_solve(muta=1, sel=1):
    pop = []
    li = list(range(DNA_SIZE))
    for i in range(POP_SIZE):
        random.shuffle(li)
        l = li.copy()
        pop.append(l)
    best_dis = []
    # 进行选择，交叉，变异，并把每代的最优个体保存在best_dis中
    for i in range(Iterations):  # 迭代N代
        pop = crossmuta(pop, CROSS_RATE, muta=muta)
        fitness = getfitness(pop)
        maxfitness = np.argmax(fitness)
        best_dis.append(distance(pop[maxfitness]))
        if sel == 1:
            pop = select(pop, fitness)  # 选择生成新的种群
        elif sel == 2:
            pop = selectII(pop, fitness)  # 选择生成新的种群

    return best_dis

# 4.1 块逆转变异策略对比测试
def opt1_test():
    ITE = 20    # 测试次数
    i_list = range(ITE)
    b_list = []     # 每次求出的最短路径
    t_list = []     # 每次求解的耗时
    b_listII = []
    t_listII = []
    b_listIII = []
    t_listIII = []

    for i in i_list:
        print(i)
        # I. 原两点互换异策略
        time_start = time.time()
        b_list.append(min(tsp_solve(muta=1)))
        time_end = time.time()
        t_list.append(time_end - time_start)
        # II. 块逆转变异策略
        time_startII = time.time()
        b_listII.append(min(tsp_solve(muta=2)))
        time_endII = time.time()
        t_listII.append(time_endII - time_startII)
        # III. 同时使用上述两种编译策略
        time_startIII = time.time()
        b_listIII.append(min(tsp_solve(muta=3)))
        time_endIII = time.time()
        t_listIII.append(time_endIII - time_startIII)

    # 做排序处理，方便比较
    b_list.sort()
    t_list.sort()
    b_listII.sort()
    t_listII.sort()
    b_listIII.sort()
    t_listIII.sort()

    ax1 = plt.subplot(121)
    ax1.plot(i_list, b_list, 'b', label="Origin")
    ax1.plot(i_list, b_listII, 'r', label="Block-reversal")
    ax1.plot(i_list, b_listIII, 'g', label="Origin + Block-reversal")
    ax1.set_ylabel("Shortest Path")
    ax2 = plt.subplot(122)
    ax2.plot(i_list, t_list, 'b', label="Origin")
    ax2.plot(i_list, t_listII, 'r', label="Block-reversal")
    ax2.plot(i_list, t_listIII, 'g', label="Origin + Block-reversal")
    ax2.set_ylabel("Cost Time")
    plt.legend()
    plt.show()

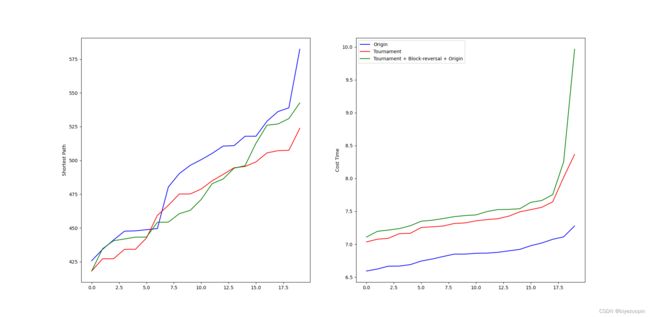
# 4.2 锦标赛选择策略对比测试
def opt2_test():
    ITE = 20  # 测试次数
    i_list = range(ITE)
    b_list = []  # 每次求出的最短路径
    t_list = []  # 每次求解的耗时
    b_listII = []
    t_listII = []
    b_listIII = []
    t_listIII = []

    for i in i_list:
        print(i)
        # I. 原赌轮盘选择策略
        time_start = time.time()
        b_list.append(min(tsp_solve(sel=1)))
        time_end = time.time()
        t_list.append(time_end - time_start)
        # II. 锦标赛选择策略
        time_startII = time.time()
        b_listII.append(min(tsp_solve(sel=2)))
        time_endII = time.time()
        t_listII.append(time_endII - time_startII)
        # III. 锦标赛选择策略 + 两点互换变异 + 块逆转变异策略
        time_startIII = time.time()
        b_listIII.append(min(tsp_solve(sel=2,muta=3)))
        time_endIII = time.time()
        t_listIII.append(time_endIII - time_startIII)

    # 做排序处理，方便比较
    b_list.sort()
    t_list.sort()
    b_listII.sort()
    t_listII.sort()
    b_listIII.sort()
    t_listIII.sort()

    ax1 = plt.subplot(121)
    ax1.plot(i_list, b_list, 'b', label="Origin")
    ax1.plot(i_list, b_listII, 'r', label="Tournament")
    ax1.plot(i_list, b_listIII, 'g', label="Tournament + Block-reversal + Origin")
    ax1.set_ylabel("Shortest Path")
    ax2 = plt.subplot(122)
    ax2.plot(i_list, t_list, 'b', label="Origin")
    ax2.plot(i_list, t_listII, 'r', label="Tournament")
    ax2.plot(i_list, t_listIII, 'g', label="Tournament + Block-reversal + Origin")
    ax2.set_ylabel("Cost Time")
    plt.legend()
    plt.show()

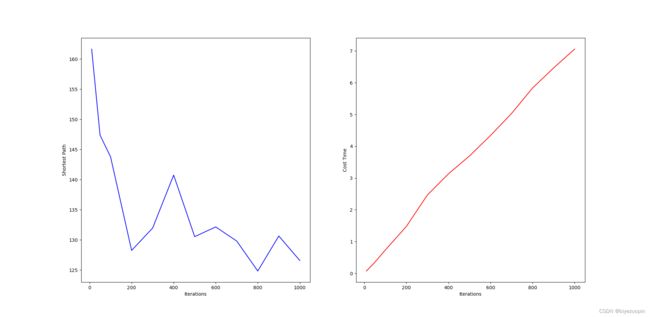
# 3.1 原程序的主函数 - 求解不同规模的TSP问题的算法性能
def ori_main():
    time_start = time.time()
    pop = [] # 生成初代种群pop
    li = list(range(DNA_SIZE))
    for i in range(POP_SIZE):
        random.shuffle(li)
        l = li.copy()
        pop.append(l)
    best_dis= []
    # 进行选择，交叉，变异，并把每代的最优个体保存在best_dis中
    for i in range(Iterations):  # 迭代N代
        pop = crossmuta(pop, CROSS_RATE)
        fitness = getfitness(pop)
        maxfitness = np.argmax(fitness)
        best_dis.append(distance(pop[maxfitness]))
        pop = select(pop, fitness)  # 选择生成新的种群

    time_end = time.time()
    print_info(pop)
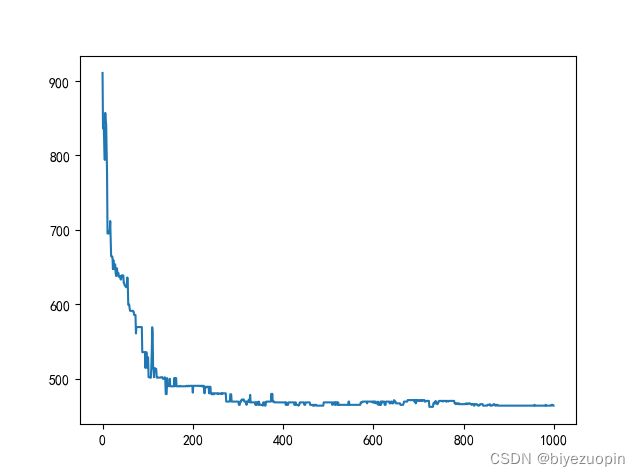
    print('逐代的最小距离：',best_dis)
    print('Totally cost is', time_end - time_start, "s")
    plt.figure()
    plt.plot(range(Iterations),best_dis)

# 4.1 块逆转变异策略运行效果展示
def opt1_main():
    time_start = time.time()
    pop = []    # 生成初代种群pop
    li = list(range(DNA_SIZE))
    for i in range(POP_SIZE):
        random.shuffle(li)
        l = li.copy()
        pop.append(l)
    best_dis= []
    # 进行选择，交叉，变异，并把每代的最优个体保存在best_dis中
    for i in range(Iterations):  # 迭代N代
        pop = crossmuta(pop, CROSS_RATE, muta=3)
        fitness = getfitness(pop)
        maxfitness = np.argmax(fitness)
        best_dis.append(distance(pop[maxfitness]))
        pop = select(pop, fitness)  # 选择生成新的种群

    time_end = time.time()
    print_info(pop)
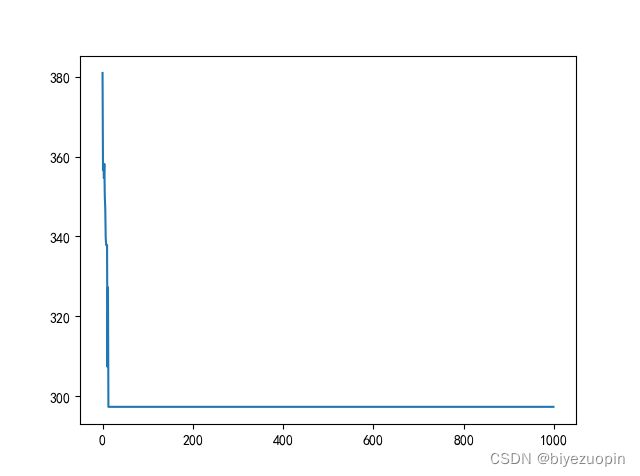
    print('逐代的最小距离：',best_dis)
    print('Totally cost is', time_end - time_start, "s")
    plt.figure()
    plt.plot(range(Iterations),best_dis)

if __name__ == "__main__":

    ori_main()    # 原程序的主函数
    opt1_main()   # 块逆转变异策略运行效果展示
    plt.show()
    plt.close()

    # opt1_test()   # 块逆转变异策略对比测试
    # opt2_test()   # 锦标赛选择策略对比测试

    # pop_size_test()       # POP_SIZE 种群规模参数测试
    # cross_rate_test()     # CROSS_RATE 交叉率参数测试
    # muta_rate_test()      # MUTA_RATE 变异率参数测试
    # cross_muta_test()     # 交叉率和变异率双参数测试